1.模糊Petri网的矩阵变换的推理算法

根据模糊Petri网的知识表达方法，结合定性绩效指标次级指标体系，建立定性绩效指标量化模糊Petri网模型，如图4-22所示。

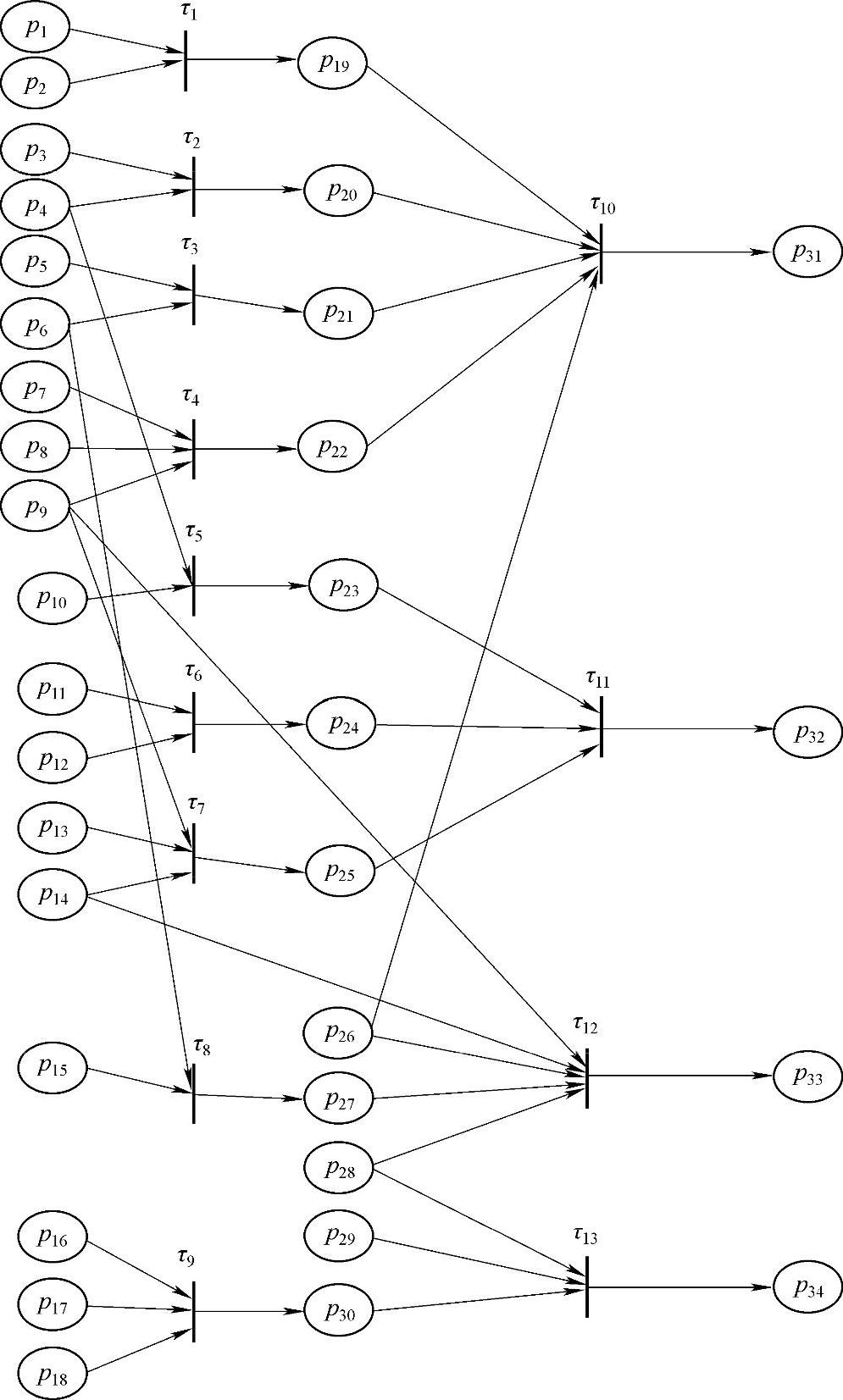
图4-22 定性绩效指标量化模糊Petri网模型

模型中各库所对应的考核指标含义和描述条件的模糊变量见表4-11。

表4-11 模型库所对应指标含义和描述条件的模糊变量表

（续）

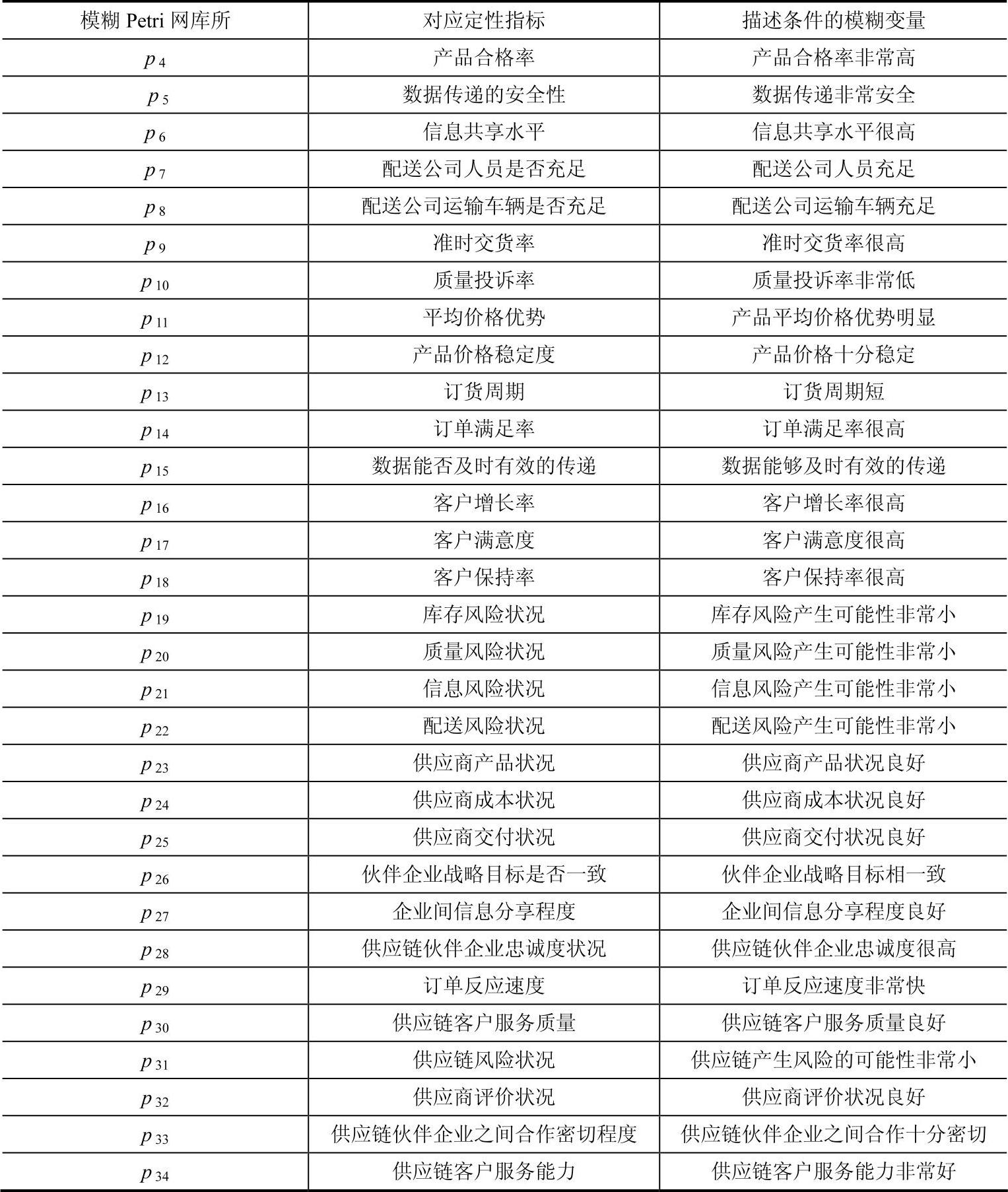
根据定性绩效指标与次级指标之间的传递关系建立了规则如下：

规则1：If库所安全水平很高（p₁，0.5750（库所对应次级指标在规则中的权重，根据4.4.3节中的算法所得））and 库存资金周转良好（p₂，0.4250），Then（τ₁=0.3（变迁阀值，根据专家经验给出））库存风险产生的可能性非常小（p₁₉，0.95（规则可信度，根据专家经验给出））。

规则2：If产品质量控制水平很高（p₃，0.6131）and产品合格率非常高（p₄，0.3869），Then（τ₂=0.4）质量风险产生可能性非常小（p₂₀，0.90）。

规则3：If数据传递非常安全（p₅，0.575）and信息共享水平很高（p₆，0.425），Then（τ₃=0.4）信息风险产生可能性非常小（p₂₁，0.98）。

规则4：If配送公司人员充足（p₇，0.4486）and配送公司运输车辆充足（p₈，0.3023）and准时交货率很高（p₉，0.2490），Then（τ₄=0.5）配送风险产生可能性非常小（p₂₂，0.96）。

规则5：If产品合格率非常高（p₄，0.6131）and质量投诉率非常低（p₁₀，0.3869），Then（τ₅=0.3）供应商产品状况良好（p₂₃，0.88）。

规则6：If产品平均价格优势明显（p₁₁，0.4250）and产品价格十分稳定（p₁₂，0.5750），Then（τ₆=0.4）供应商成本状况良好（p₂₄，0.92）。

规则7：If准时交货率很高（p₉，0.4109）and订货周期短（p₁₃，0.3521）and订单满足率很高（p₁₄，0.2371），Then（τ₇=0.5）供应商交付状况良好（p₂₅，0.85）。

规则8：If信息共享水平很高（p₆，0.5750）and数据能够及时有效的传递（p₁₅，0.4250），Then（τ₈=0.3）企业间信息分享程度良好（p₂₇，0.90）。

规则9：If客户增长率很高（p₁₆，0.2281）and客户满意度很高（p₁₇，0.4743）and客户保持率很高（p₁₈，0.2975），Then（τ₉=0.3）供应链客户服务质量良好（p₂₅，0.92）。

规则10：If库存风险产生可能性非常小（p₁₉，0.2863）and质量风险产生可能性非常小（p₂₀，0.2433）and信息风险产生可能性非常小（p₂₁，0.2017）and配送风险产生可能性非常小（p₂₂，0.1483）and伙伴企业战略目标相一致（p₂₆，0.1204），Then（τ₁₀=0.4）供应链产生风险的可能性非常小（p₃₁，0.88）。

规则11：If供应商产品状况良好（p₂₃，0.2281）and供应商成本状况良好（p₂₄，0.4743）and供应商交付状况良好（p₂₅，0.2975），Then（τ₁₁=0.4）供应商评价状况良好（p₃₂，0.9）。

规则12：If准时交货率很高（p₉，0.1837）and订单满足率很高（p₁₄，0.1642）and伙伴企业战略目标相一致（p₂₆，0.2380）and企业间信息分享程度良好（p₂₇，0.2380）and供应链伙伴企业忠诚度很高（p₂₈，0.1762），Then（τ₁₂=0.5）供应链伙伴企业之间合作十分密切（p₃₃，0.95）。

规则13：If供应链伙伴企业忠诚度很高（p₂₈，0.2281）and订单反应速度非常快（p₂₉，0.2975）and供应链客户服务质量良好（p₃₀，0.4743），Then（τ₁₃=0.5）供应链客户服务能力非常好（p₃₄，0.9）。

通过对连锁零售企业精益供应链的定性绩效指标进行调研获得数据，采用4.4.2节中所阐述的直接模糊统计法和区间法得到的相对隶属度函数对调研后的数据进行模糊处理，可得到库所的初始可信度S₀为

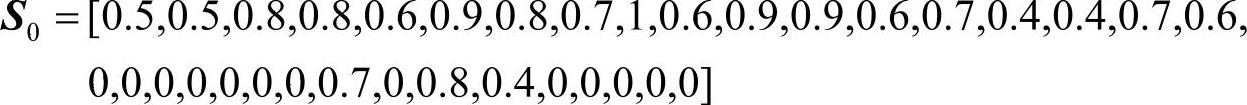
通过4.4.3节中算法可以确定每个模糊命题在规则中的权重，如规则1中2个模糊命题：库所安全水平很高（p₁，0.5750）、库存资金周转良好（p₂，0.4250）所对应的权重分别为0.5750和0.4250。根据规则之间的相互关系可以得到模糊Petri网模型的输入矩阵Δ_n×m：

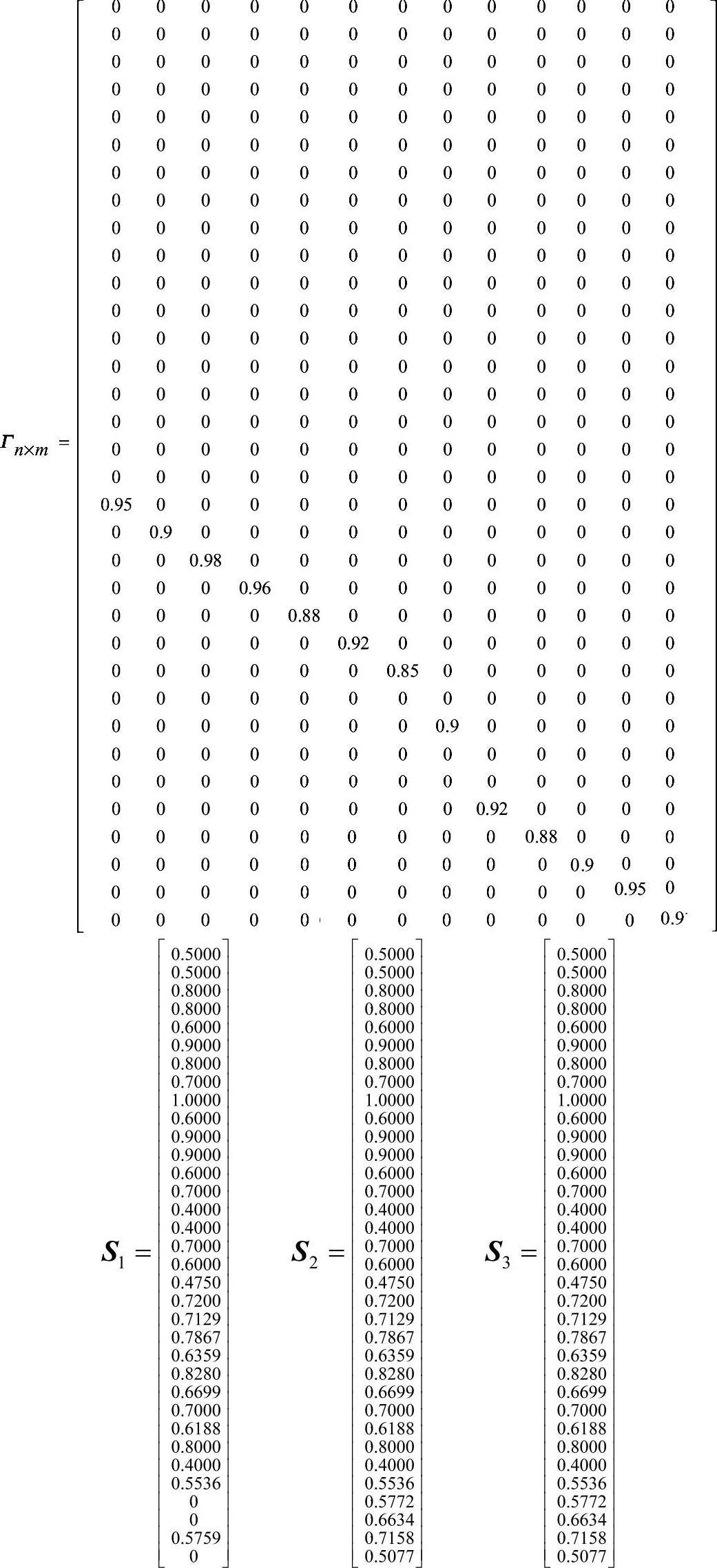
根据专家经验可以得到规则可信度矩阵（即输出矩阵Γ_n×m）和阈值向量τ为τ=[0.3，0.4，0.4，0.5，0.3，0.4，0.5，0.3，0.3，0.4，0.4，0.5，0.5]

根据前文阐述的模糊Petri网的形式化推理算法，将初始可信度向量S₀、输入矩阵Δ_n×m、输出矩阵Γ_n×m和阈值向量τ代入公式（4-1）中进行推理运算。利用Matlab对模糊Petri网矩阵进行计算，结果为

(www.daowen.com)

经过3轮迭代，模糊Petri网的状态向量不再发生变化，表明推理结束，最终结果为

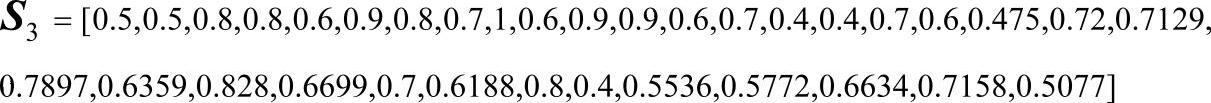
根据计算的最终结果可以得到4个定性绩效评价指标：供应链风险、供应链客户服务能力、供应商评价、供应链伙伴企业之间合作密切程度的量化数据分别为S₃（p₃₁）=0.5772、S₃（p₃₂）=0.6634、S₃（p₃₃）=0.7158和S₃（p₃₄）=0.5077。

以供应链风险为例，S₃（p₃₁）=0.5772表明库所p₃₁描述的模糊命题的最终可信度为0.5772，通过表4-1可知，库所p₃₁所代表的模糊命题为“供应链产生风险的可能性非常小”，则说明该连锁企业供应链发生风险的可能性很小的可信度为0.5772。由于S（p_i）∈[0，1]（i=1，2，…，n），则当S（p_i）的取值越趋近于1时，说明命题的真实程度越高。若S₃（p₃₁）越趋近于1，则“供应链产生风险的可能性非常小”越可信，说明供应链不容易发生风险。由于供应链风险与供应链绩效的相关性，故供应链风险的可信度可以用于供应链绩效的评估。

此外，通过定性绩效指标量化模糊Petri网模型可以发现，定性绩效指标的次级考核指标之间存在一定的耦合性和并发性。如库所p₄代表的模糊命题“产品合格率非常高”，不仅是库所p₃₁（供应链风险状况）的根库所，同时也是库所p₃₂（供应商评价状况）的根库所。当库所p₃₁的初始可信度值发生变化时，不仅可以导致S（p₃₁）的改变，而且会影响库所p₃₂的最终计算结果。如以下算例，当S₀（p₄）由0.8下降为0.6时，S₃改变为

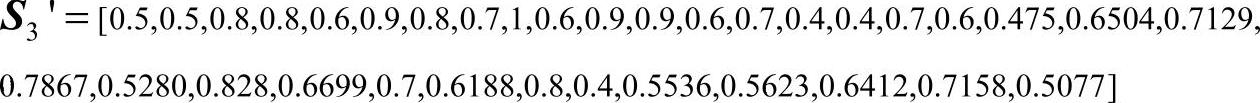
模糊Petri网模型全部库所可信度在S₀（p₄）改变前后的变化情况如图4-23所示。

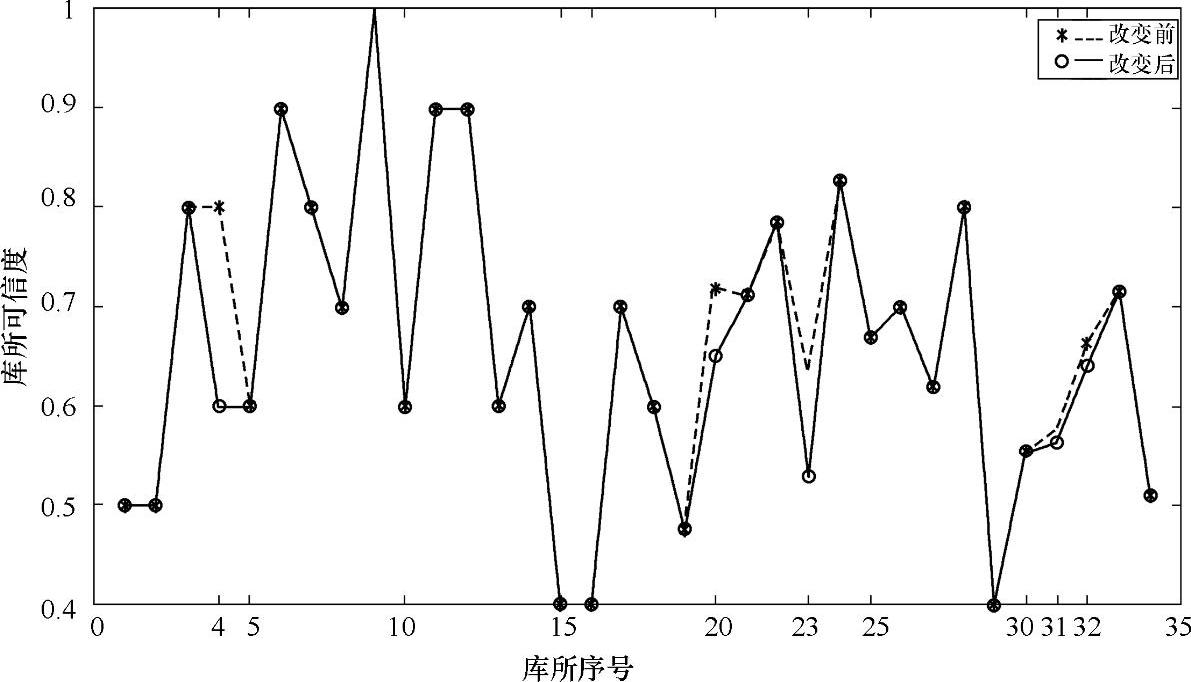
图4-23 库所p₄可信度改变前后计算结果对比

图中多处曲线无法重合的现象表明当一个库所的可信度发生变化时，由于耦合性和并发性的存在，导致多个库所的计算结果出现变化。

在实际过程应用中，如果不能妥善处理具有并发性和耦合性的库所，可能导致最终计算结果的错误。由于模糊Petri网能够合理有效地处理并发性问题，因此在推理过程中保证了数据准确性。

2.模糊Petri网的逆向推理诊断分析

魏勇等（2011）提出的命题可信度分类和对应数值范围，可以将定性绩效指标量化模糊Petri网模型中库所的可信度分类见表4-12。

表4-12 量化模糊Petri网模型中库所的可信度分类表

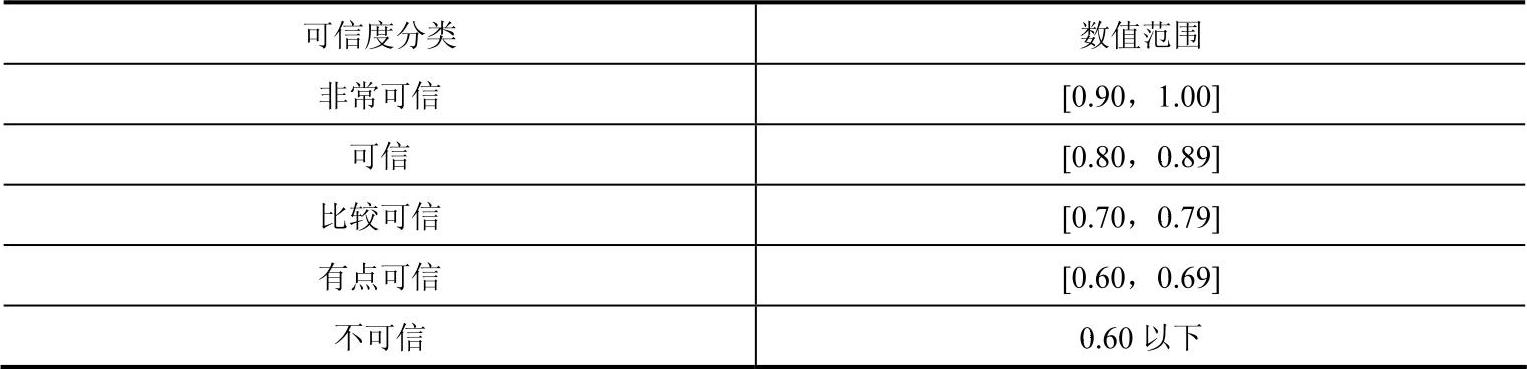
根据表4-12可知，当S（p_i）＜0.6（i=1，2，…，n），该库所所代表的模糊命题为不可信状态。如S₃（p₃₄）=0.5077＜0.6，说明“供应链客户服务能力非常好”为不可信，这就意味着供应链客户服务能力方面存在某些问题，从而导致供应链客户服务能力下降，进而使得供应链客户服务能力非常好呈现不可信的状态。供应链客户服务能力表现不好，同时也会对整体供应链绩效产生负面影响。模糊Petri网的逆向推理诊断分析就是基于找到问题产生的根源从而进一步解决问题提高整体绩效水平的目的而提出的。

根据本章中前面介绍的模糊Petri网的逆向诊断算法，首先确定量化模糊Petri网模型中的根库所集RP为

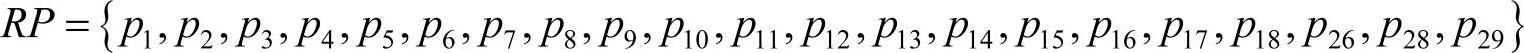
目标库所集GP为

GP={p₃₁，p₃₂，p₃₃，p₃₄，}

模型中各个库所的ISR见表4-13。

表4-13 量化模糊Petri网模型中库所所对应的ISR表

（续）

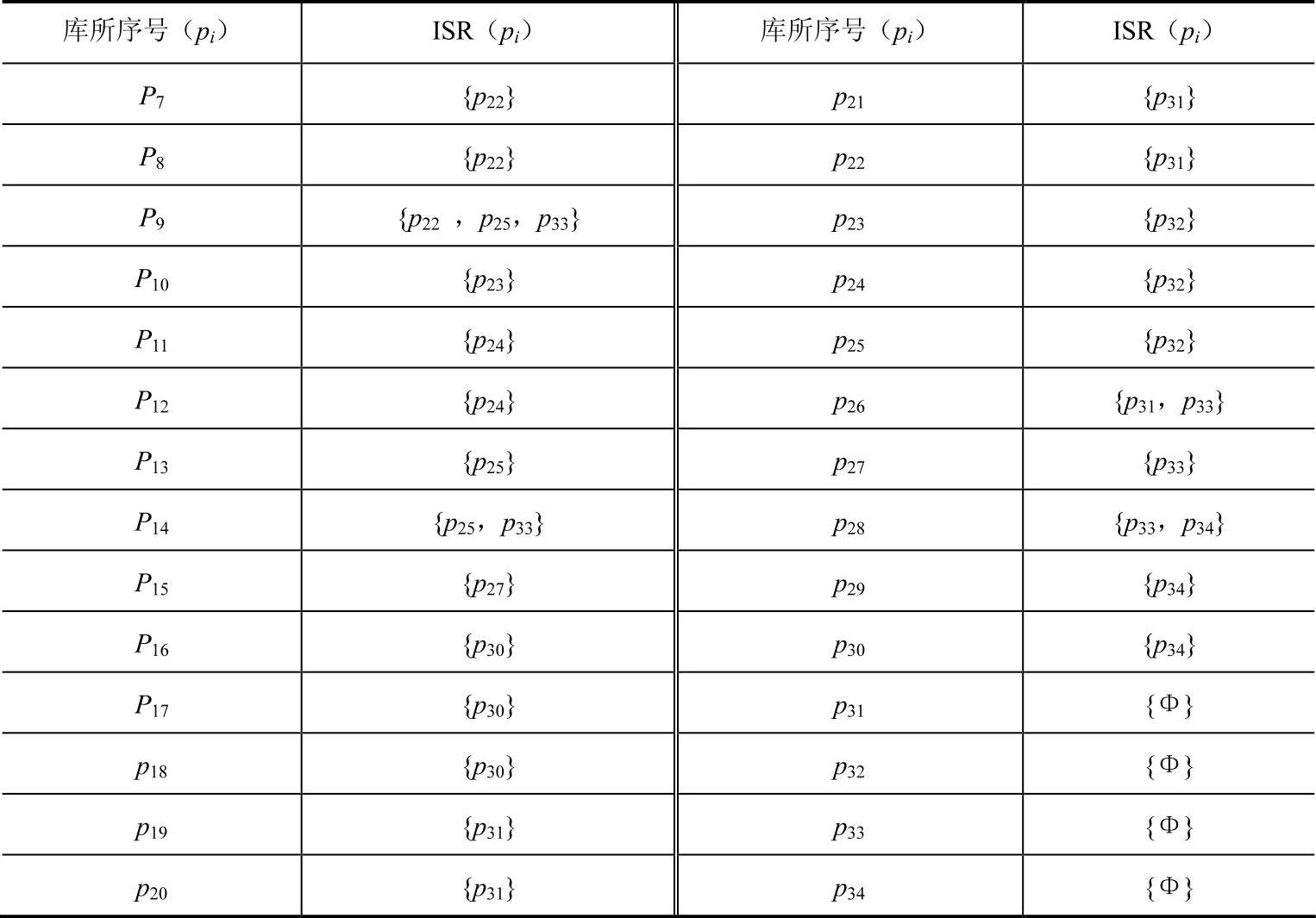
设当推理完毕后，若存在S（GP（p_i））＜0.6，则启动逆向诊断算法。根据计算结果可知，S₃（p₃₁）=0.5772和S₃（p₃₄）=0.5077满足条件。令p_v=p₃₁，根据逆向诊断算法得到E={p₁₉，p₂₀，p₂₁，p₂₂，p₂₆}，Q={p₂₆}，即库所p₂₆为导致“供应链产生风险的可能性非常小”不可信的来源库所；同理可得库所p₂₉为导致“供应链客户服务能力非常好”不可信的来源库所。库所p₂₆和库所p₂₉所对应的次级指标分别为“伙伴企业战略目标是否一致”、“订单反应速度”。计算结果表明，“伙伴企业战略目标是否一致”和“订单反应速度”是导致目标库所不可信的最主要原因，同时也是当前最亟须解决的问题所在。供应链管理者应根据此计算结果并结合实际情况提出相应解决方案，从而使得供应链风险和供应链客户服务能力两方面得到改善，进一步提高整体供应链的绩效水平。