在定性指标FPN量化模型中，输入矩阵Δ_n×m表示每个次级指标被赋予的权重，它代表了定性指标的不同次级指标对该定性指标最终评价的影响能力的贡献性大小。在实际推理过程中，权重的大小往往需要由领域内专家给出，这样在较大程度上存在着主观和人为的因素，因此依据魏勇等（2011）的研究文献可知，在多个规则组合的可信度计算中可能会产生较大的误差，甚至导致最终结论的不可信。而采用程启月等（2011）提出的主观赋值法与客观赋值法相结合的“结构熵权法”确定模糊Petri网中每个次级指标的权重，结论综合了主观偏好及客观度量的互补特性，计算权重的具体步骤如下：

第一步，按照“德菲尔法”采集k个专家意见，形成专家对同一规则下n个次级指标d_j={d₁，d₂，…，d_n}“贡献性”大小的“典型排序”。利用自然数{1，2，…，n}依次表示每个次级指标的“贡献性”大小，即1表示“贡献最大”，2表示“贡献非常大”，以此类推。假设有3组专家对供应商评价中的成本、交付和产品的“贡献性”大小进行排序，见表4-9，表中“√”代表专家的选择判断。

表4-9 指标贡献性排序调查表

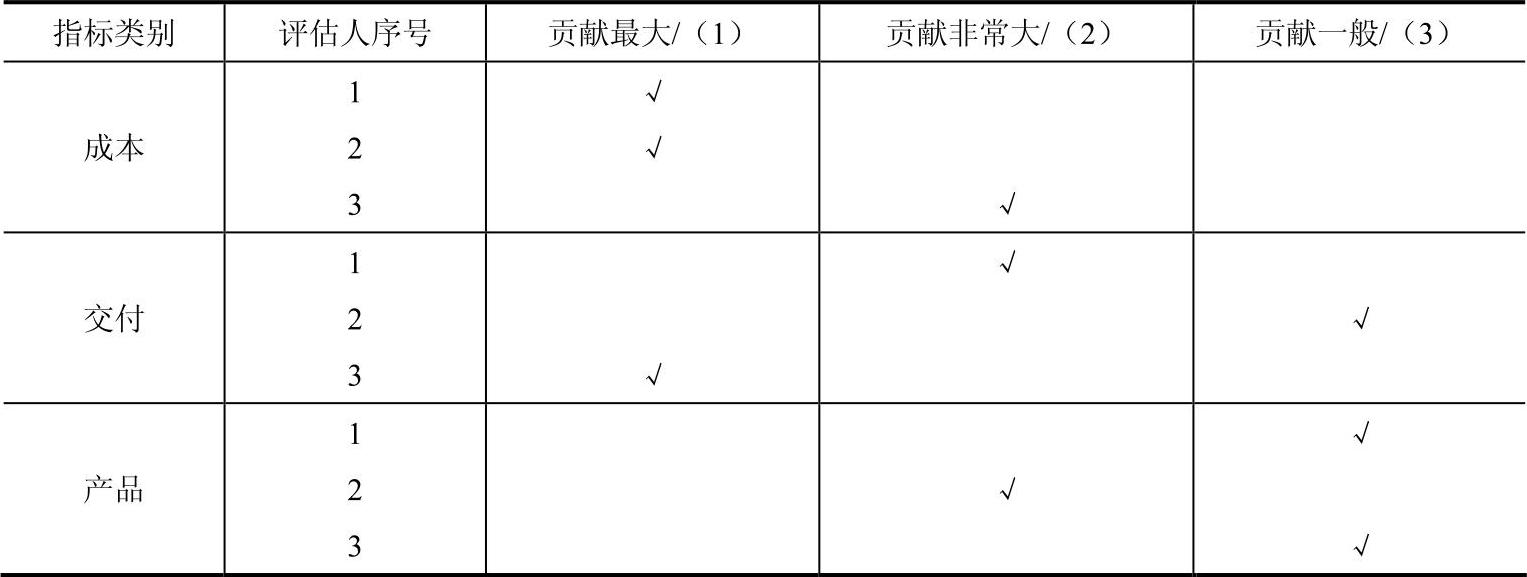
第二步，根据表4-9中专家判断形成的“典型排序”结果，可以得到次级指标d_j的典型排序矩阵：A=（a_ij）_k×n。式中，a_ij表示第i个专家对于第j个指标的贡献性”大小判断结果，用自然数{1，2，…，n}表示。表4-9中，a₁₁表示为第一位专家对第一个指标（成本）的贡献性大小认定为“贡献最大”，则a₁₁所对应的自然数为1。

第三步，根据熵理论推导出：

具体推导过程详见程启月等研究文献。利用式（4-8）对“典型排序”进行定性与定量的转化，得到隶属度矩阵：B=（b_ij）_k×n。式中，µ（a_ij）表示“典型排序”对应的隶属度值；m为转化参数量，取m=n+2，故b_ij=µ（a_ij）。

第四步，根据计算公式，即

计算k个专家对于同一次级指标的平均认知程度。

第五步，由于不同专家对于事物的认知不同，因此为了描述专家对次级指标d_j的由于认知而产生的不确定性，定义Q_j，则：(www.daowen.com)

Q_j=max（b_1j+b_2j+…b_nj）-b_j （4-10）

计算参加问卷调查的k个专家对于每个次级指标的总体认知程度，记为x_j，则：

x_j=b_j（1-Q_j） （4-11）

第六步，对x_j进行归一化处理，令归一化的结果记为α_j，则：

最终，可得到代表n个次级指标d_j对于定性指标最终评价的影响能力的贡献大小的权重集W={α₁，α₂，…，α_n}。

通过结构熵权法得到权重集W，在充分考虑专家主观经验偏好的基础上，利用熵理论对“典型排序”进行“盲度分析”，从而消除“典型排序”中出现的数据“噪声”并减少了源数据的不确定性，使得权重集更具客观性。

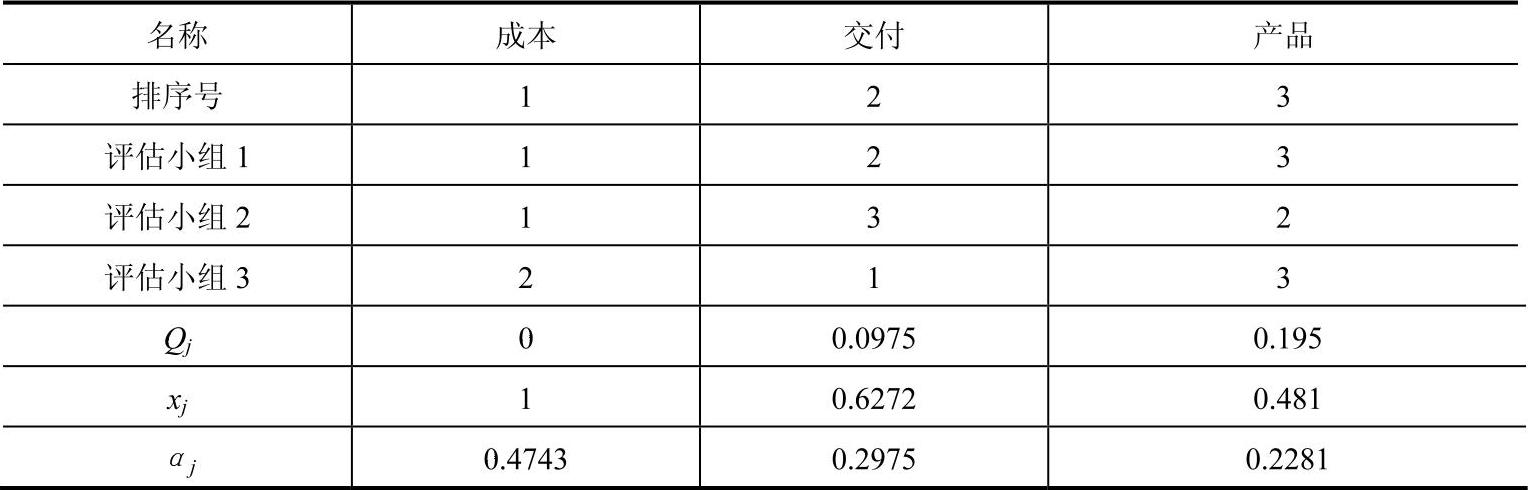
按照上述“结构熵权法”的算法，结合表4-9内专家对供应商评价中的成本、交付和产品的“贡献性”大小进行排序结果，可以得到关于成本、交付和产品的“典型排序”和对应权重系数见表4-10。

表4-10 供应商评价指标“典型排序”和权重系数表