在利用模糊Petri网对定性绩效指标进行量化过程中，首先需要确定每个库所节点在推理开始时的初始状态S₀（p），才能根据FPN正向推理量化算法进行计算，从而得到定性指标的量化结果。

应用模糊Petri网时，由于模糊Petri网的根库所代表了以模糊命题形式给出的供应链定性绩效指标的最低一级考核指标，而根库所中token的取值就表示该命题所描述的模糊语言变量的隶属度。在模糊Petri网推理过程中，最终目标库所的取值是根据根库所中token的取值所推理得到，因此需要采用隶属函数方法来获取根库所中token的隶属度值。然而，由于不同考核指标可能采取不同的衡量标准，不同指标间所参考的数据意义、量纲、考察方法也均不尽相同，因此需要根据实际情况构建不同的“绩效指标隶属度函数”计算所对应命题的隶属度，故这里设计两种隶属度函数对应于不同形式的考核指标。

1.直接模糊统计法确定绩效指标隶属度函数

实际绩效评价中比较普遍的采用“专家打分”形式对某类绩效考核指标的好坏进行衡量，这种方法又可以称为等级描述法，此类“专家打分”形式所产生的数据均为离散型。具体操作中，可以按照“优秀”、“良好”、“及格”、“不及格”等级别对指标进行评判打分，每个级别有与之对应的分数段。如某供应链企业请专家对该企业的若干供应商在某段时间内的产品质量控制水平进行打分，打分标准见表4-4。

表4-4 产品质量控制水平的打分标准

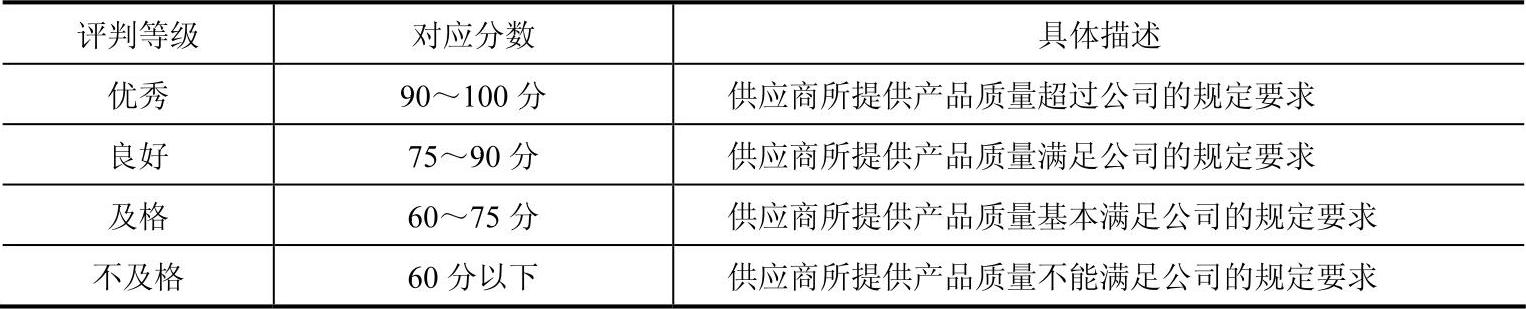
针对上述类型的考核指标，可利用直接模糊统计法确定其定对应库所的初始可信度的相对隶属度函数，用于对连锁零售企业中的模糊描述进行量化分析。直接模糊统计法的基本步骤如下：

1）根据某次打分结果进行排名，将排名前k位的隶属度定为1，将排名最后k位的隶属度定为0，其余结果的隶属度在（0，1）之间进行线性插值，得到如图4-18所示“半梯形”曲线µ（x），并找出使得曲线µ（x）=0和µ（x）=1的点a、b，即µ（a）=0，µ（b）=1。具体k值可根据实际参加打分的成员数量决定。

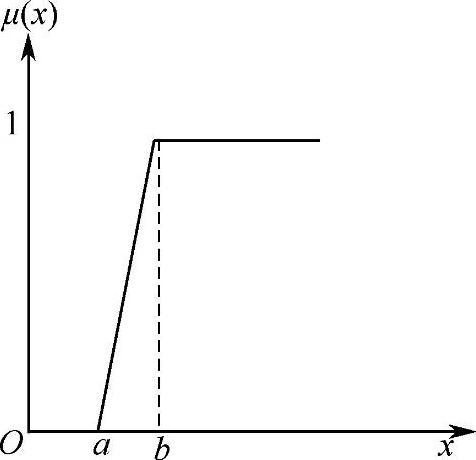
图4-18 相对隶属度简图

2）假设打分一共进行了n次，按照步骤1，即存在µ₁（x），…，µ_n（x），与之对应的点a₁，…，a_n，b₁，…，b_n。依次计算各点在每次打分的相对隶属度µ_ij（x），即

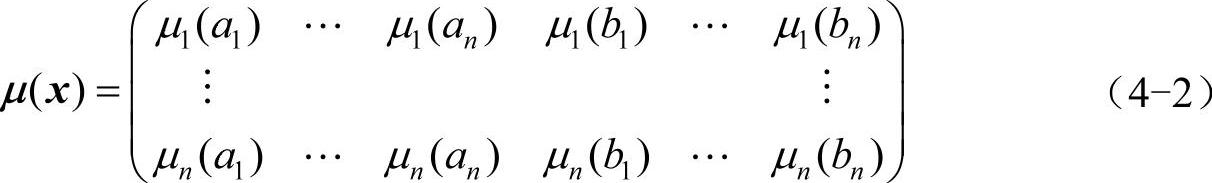
3）按照式4-2计算n次的相对隶属度，式中n表示为打分的总次数，µ_ij（x）表示每次得分的相对隶属度，M（µ_j）为n次打分的平均隶属度，i=1，…，n，j=1，…，2n。

4）将a₁，…，a_n和b₁，…，b_n按照大小顺序排列，从而在0～100分内得到若干组区间，根据每个点的平均隶属度M（µ_j）在区间上进行分段线性插值。

按照上述算法，考察位于华北的10家连锁零售企业的供应商产品质量控制水平。设每季度专家会对这些企业的供应商在该季度的产品质量控制水平表现进行考评，具体考评手段为打分（0～100）。2000年某季度的企业供应商产品质量控制水平得分见表4-5。

表4-5 2000年某季度企业供应商产品质量控制水平得分表

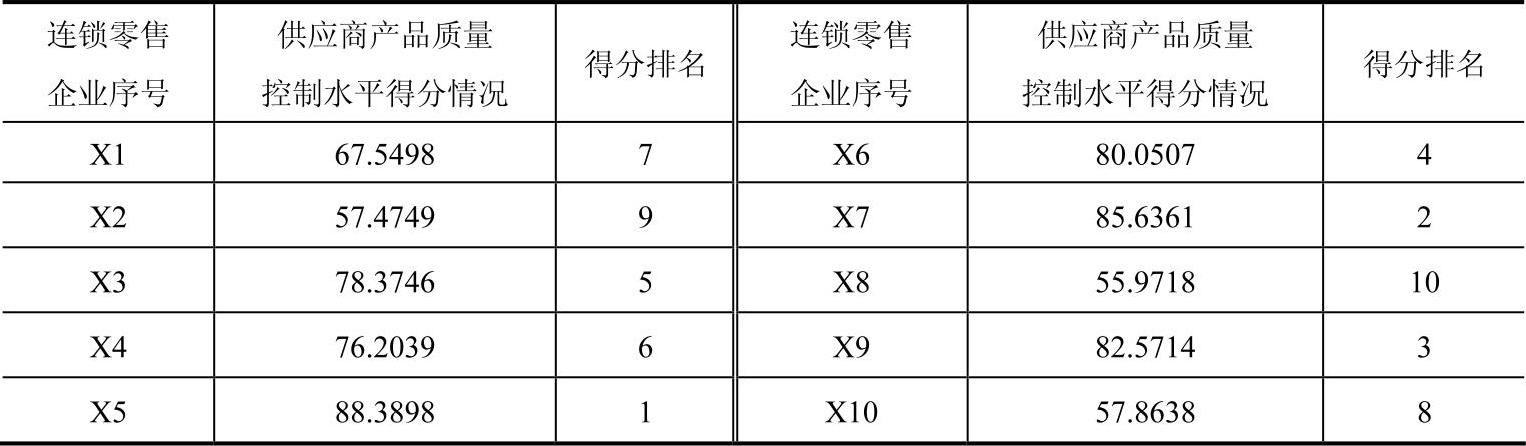
按照直接模糊统计法给出的步骤1，设k=2，则得到2000年该季度专家打分的相对隶属度曲线，如图4-19所示。根据曲线可知a=57.4749，b=85.6361。

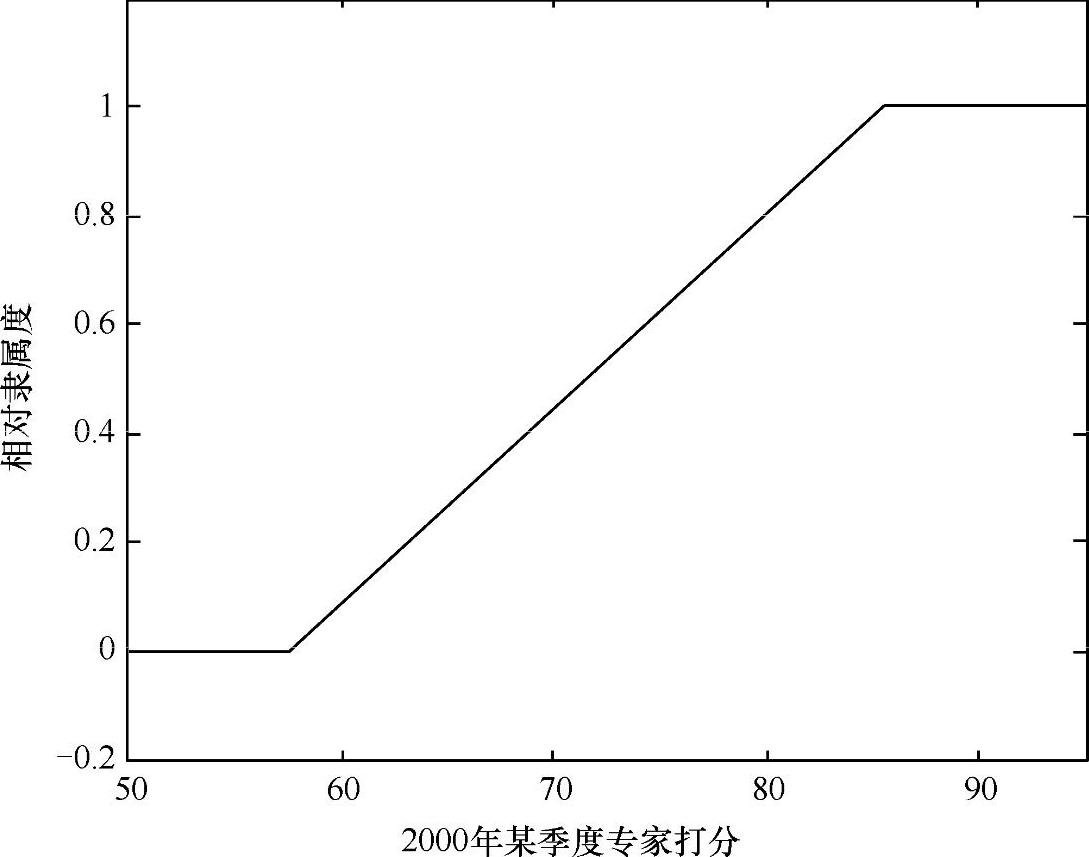
图4-19 2000年某季度的企业供应商产品质量控制水平相对隶属度简图

依据直接模糊统计算法步骤2-4，将2000～2002年按季度对供应商产品质量控制水平情况进行统计，表4-6为2000～2002年供应商产品质量控制水平得分，依据数据得到的相应隶属度曲线如图4-20。

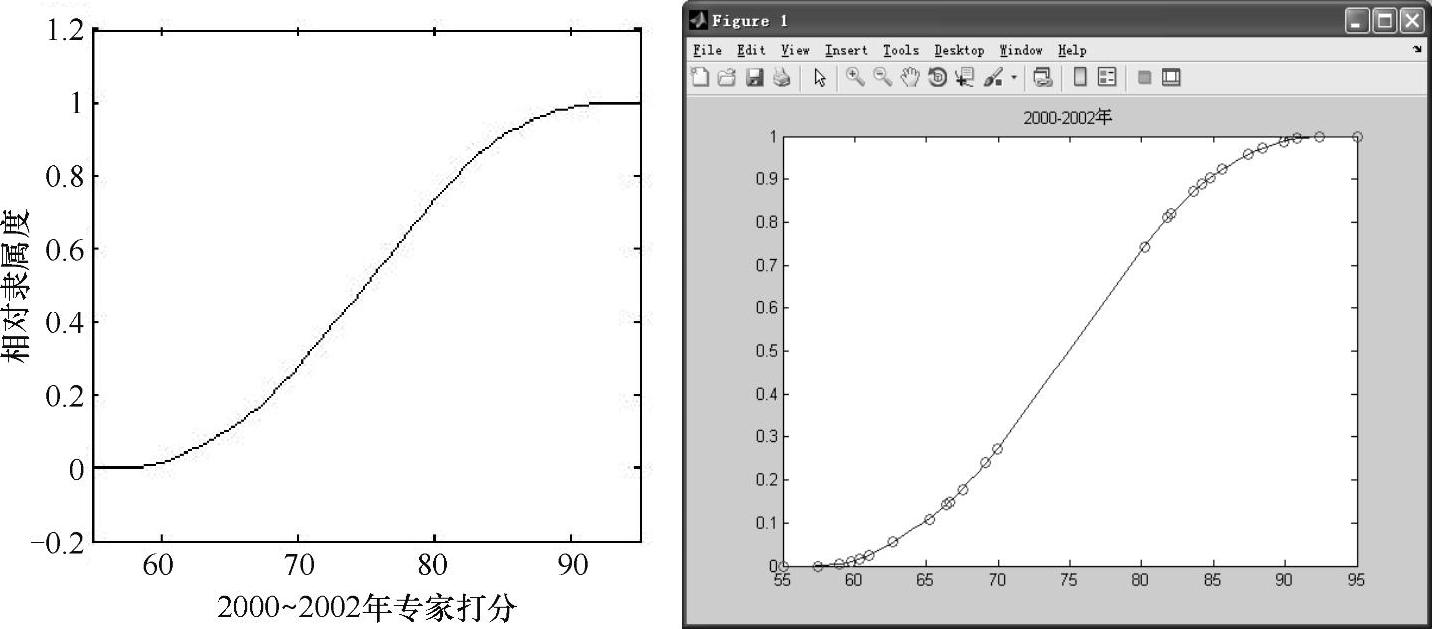
图4-20 2000～2002年供应商产品质量控制水平相对隶属度

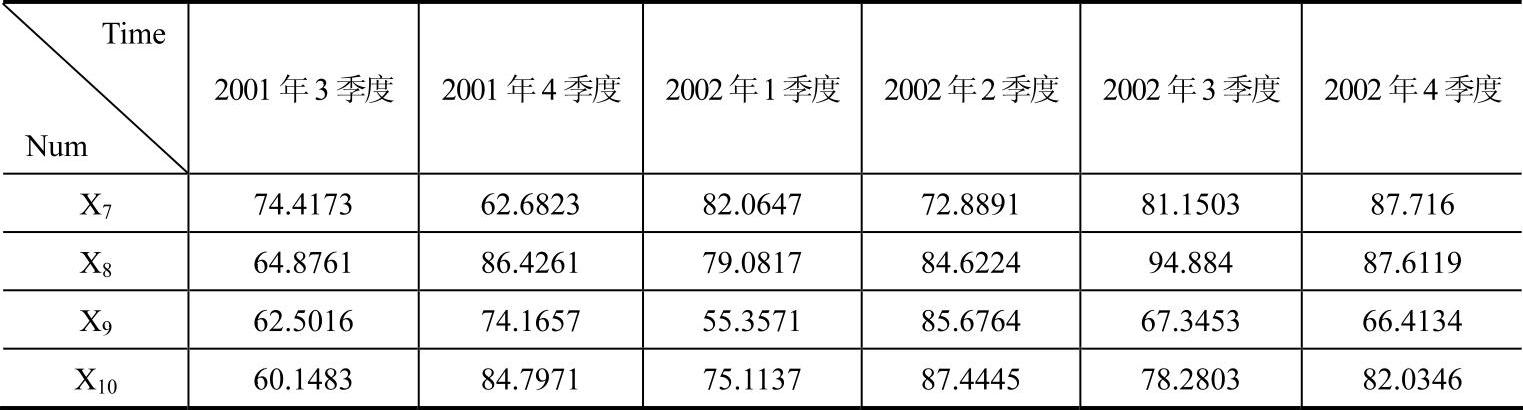
表4-6 2000～2002年企业供应商产品质量控制水平得分表

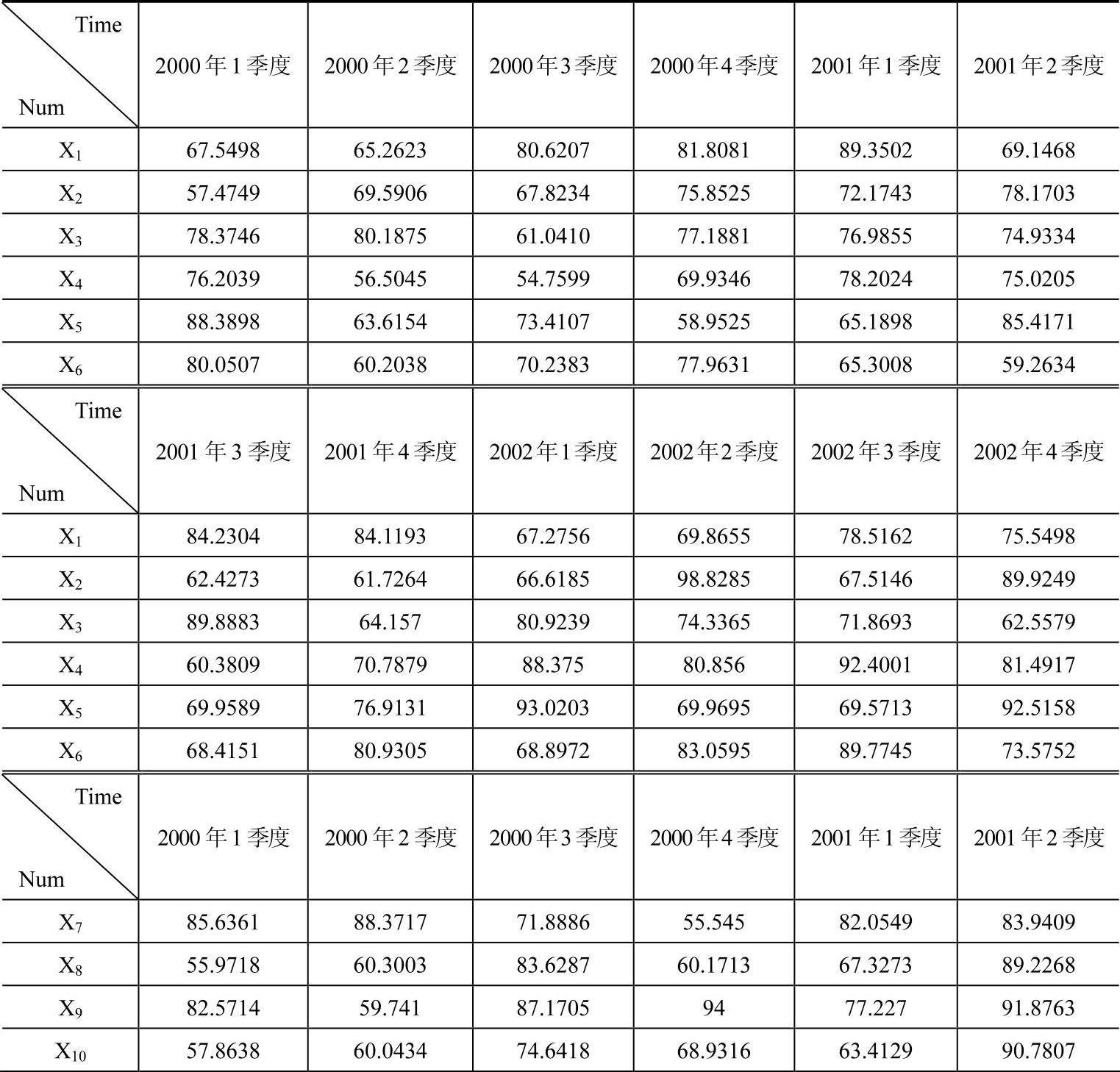
（续）

利用该隶属度曲线可以对模糊变量进行隶属度量化，比如2002年专家对某企业的供应商产品质量控制水平打分为80分，那么由图4-20将对利用隶属度函数进行量化，可以得到该企业供应商产品质量控制水平为好的隶属度为0.7338。(www.daowen.com)

由模糊统计的结果可以看出：

1）单个季度的相对隶属度曲线是“阶梯”型（或者半梯形）的，而对若干季度的打分进行直接模糊统计后，相对隶属度曲线趋近于Sigmoid函数，且随着统计次数n的增大，隶属度曲线会逐渐地稳定。

2）由于最终的相对隶属度函数是n次打分的统计平均值，每次每名专家的打分情况都会对最终的隶属度函数有影响。

3）易知，当对供应商产品质量控制水平好的评价随时间发生变化时，相对隶属度函数也会随之发生调整，即每一次新的打分都会对原先的隶属度函数进行修正。

2.区间法确定绩效指标隶属度函数

在定性指标量化过程中，专业人士可能针对某次级指标所对应的“模糊命题”给出对应的判断区间，例如“单件产品价格稳定”的判断区间为“15～20元”，很明显此类判断区间属于连续性数据。谢倩等（2012）给出了确定连续型变量库所模糊token的方法，但是在应用时存在若干缺陷：文献中所定义论域U=[a_min，b_max]的上下限差值（即b_max-a_min+1）为质数时，算法结果会导致出现丢失数据点的情况；所给出的具体操作在实际应用中会受到限制。因此，本节在已有研究的基础上，将算法改进如下：

设每个专业人士所给出的描述模糊变量的区间为U_i=[a_i，b_i]（i=1，…，n，n为专业人士个数）。

1）判断区间U_i的取值，从而得到最小值、最大值分别为a_min，b_max，若b_max-a_min为10的整数倍，则数据保持不变，论域为U=[a_min，b_max]；否则，扩大整体数据的量纲，设扩大后新产生的最小值、最大值分别为na_min、nb_max，满足nb_max-na_min为10的整数倍，论域为U=[na_min，nb_max]。

2）将论域U划分为k等分，这里k统一取10，则论域U被划分为10个相邻区间U_j[s_j，w_j）（j=1，…，10），区间长度q为

q=（b_max-a_min）/n （4-4）

3）计算Xi_Uj，Xi_Uj表示专业人士i所给出区间内的值，在以d为间隔在U_j中出现的频次，其中d表示增量步长且d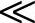（b_max-a_min）：

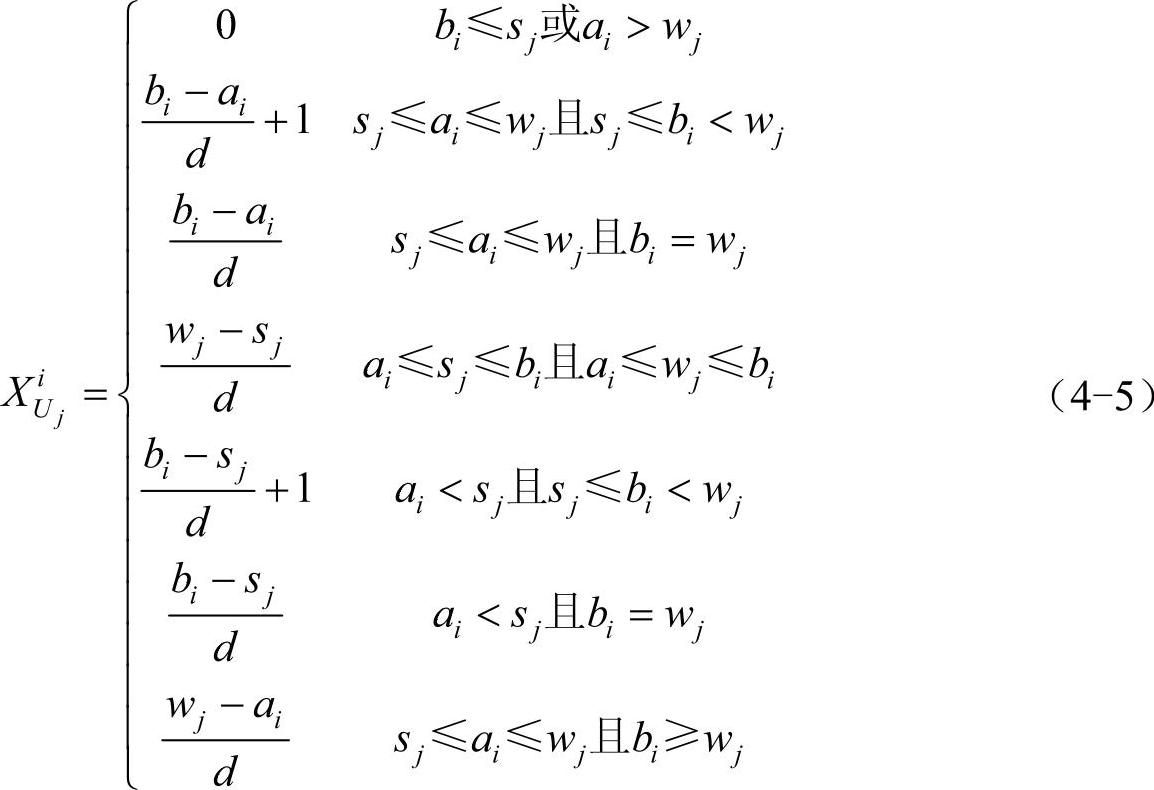
4）计算n位专业人士在区间U_j出现的总频次，此步体现了所有专业人士对于该次级指标所对应的模糊命题的总体判断：

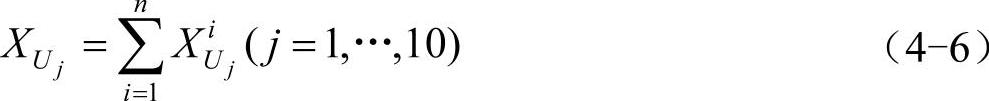
5）计算相对频次µ_j，该步骤体现了专业人士对于该次级指标所对应的模糊命题的平均判断：

6）确定模糊连续型变量库所模糊token的隶属度，模糊token的隶属度为min{µ_j，1}。

在上述算法中，首先d取值越小越好，在这里为了计算方便统一取d=1。其次，所谓扩大整体数据量纲目的是为了保证扩大后的论域可以被10整除，从而不会出现丢失数据的情况。比如，论域为U=[0.05，0.13]，可以将0.05取为50×10^-3，0.13取为130×10^-3，则新得到的论域为U=[50，130]。这样不仅可以保证隶属度函数连续不漏点，而且量纲扩大后的数据其物理意义没有发生任何变化。最后，统一k的取值为10可以使得实际应用比较方便，不需要在每次数据发生变化后重新定义k值。

以谢倩等（2012）中的数据为例，设存在10位专业人士对“单件产品价格稳定”给出判断区间，判断者结果调查表见表4-7。

表4-7 判断者结果调查表

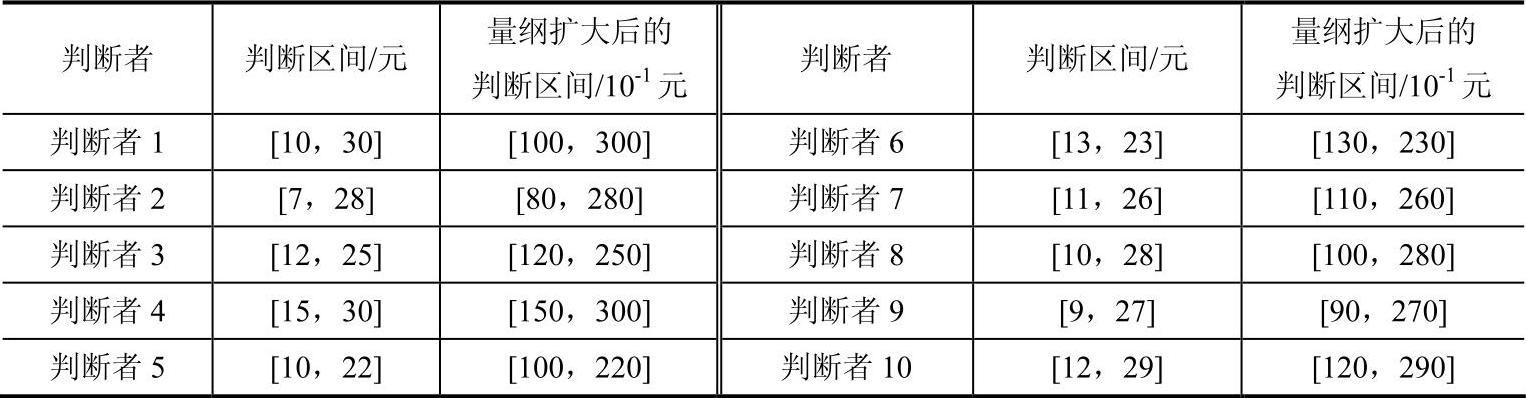
根据上文改进算法步骤1，论域为U=[7，30]，将整体数据量纲扩大，结果见表4-7，则新的论域为U=[70，300]，由于k统一取10，则区间长度q=23。按照上述给出的算法得到描述该命题的隶属函数为µ（x），如图4-21所示：

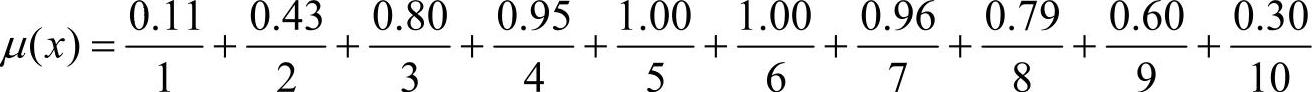
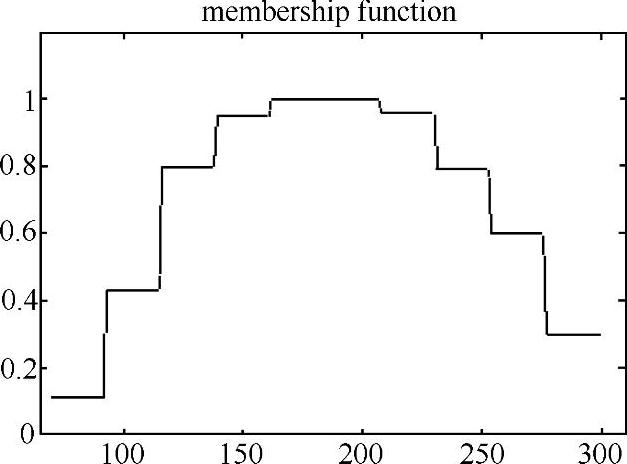
图4-21 描述模糊命题的隶属函数曲线

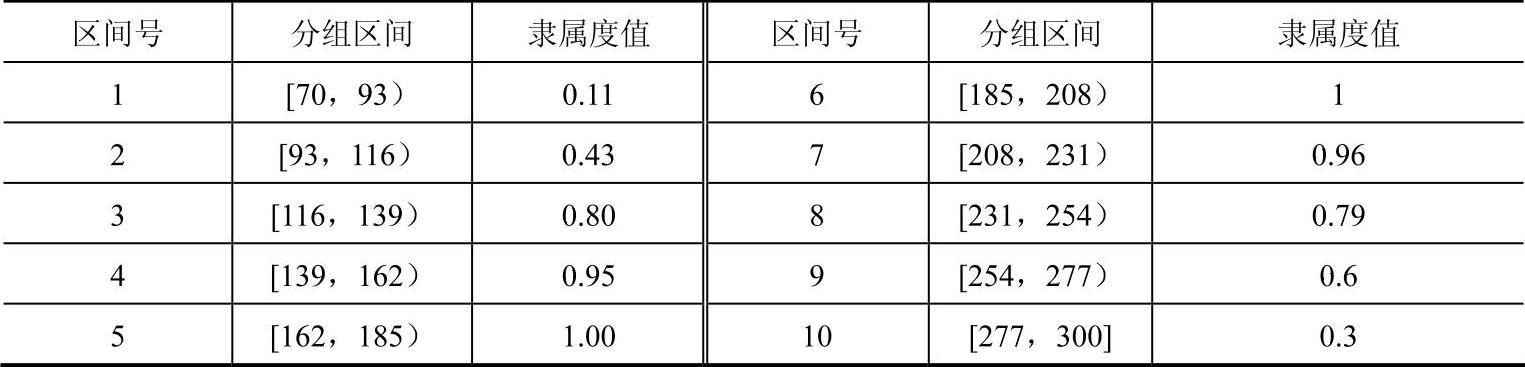
采用上述算法得到模糊统计结果见表4-8，若该产品的价格取值为150时，由表中可知150属于区间4，故该模糊命题的所对应库所的token隶属度为0.95。

表4-8 模糊统计结果表