Petri网是以研究模型系统的组织结构和动态行为为目标的，它着眼于系统中可能发生的各种状态变化以及变化之间的关系。

基本Petri网包括：库所、变迁、输入函数、输出函数四个部分，即PNS=（P，T，I，O）。也可把输入函数和输出函数合并，将Petri网分为：库所、变迁和弧三个部分。将其用字母表示如下：

1）P={p₁，p₂，p₃，…，p_n}是库所的有限集合，n＞0为库所的个数；

2）T={t₁，t₂，t₃，…，t_m}是变迁的有限集合，m＞0为变迁的个数；

3）I：P×T→N是输入函数，它定义了从P到T的有向弧的重复数或权的集合，这里N{0，1…}为非负整数集；

4）O：T×P→N是输出函数，它定义了从T到P的有向弧的重复数或权的集合。

在Petri网的形式化表示方法中，动作称为变迁，用方框、粗杆表示；发生条件称为库所，用圆圈、椭圆表示。文献中一般以⋅t表示t的输入库所，t⋅表示输出库所，同理以⋅p和p⋅分别表示输入输出变迁。某一库所表示的局部状态的实现情况用库所中所包含的托肯（token）数目（m（p））来表示。在Petri网中，用库所中的小圆点表示托肯。库所、变迁和它们之间的输入函数、输出函数一起形成了网。

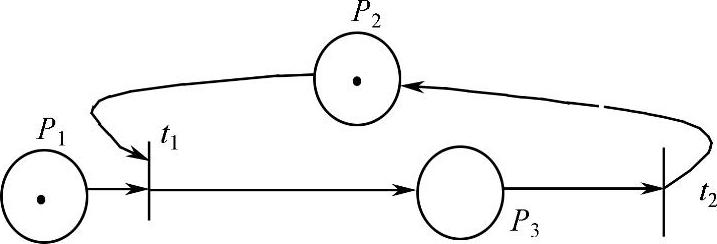
图4-1所示为一个简单的Petri网结构图。

(www.daowen.com)

图4-1 简单的Petri网结构图

图4-1中，P₁、P₂、P₃为库所，t₁、t₂为变迁，连接库所与变迁，由库所指向变迁的称为为输入函数，由变迁指向库所的称为输出函数。其中P₁和P₂各有一个托肯，由使能定义：一变迁t∈T在标示m下使能，当且仅当：∀p∈⋅t：m（p）≥I（p，t），此处∀表示“对于所有的”，在图中可见，⋅t₁={p₁，p₂}，由于m（p₁）=1≥I（p₁，t₁）=1，m（p₂）=1≥I（p₂，t₁），因此t₁使能；而⋅t={p₃}，由于m（p₃）＜I（p₃，t₂）=1，因此t₂不使能^[3]。当变迁t₁激发后，Petri网的托肯值便发生了变化，如图4-2所示。

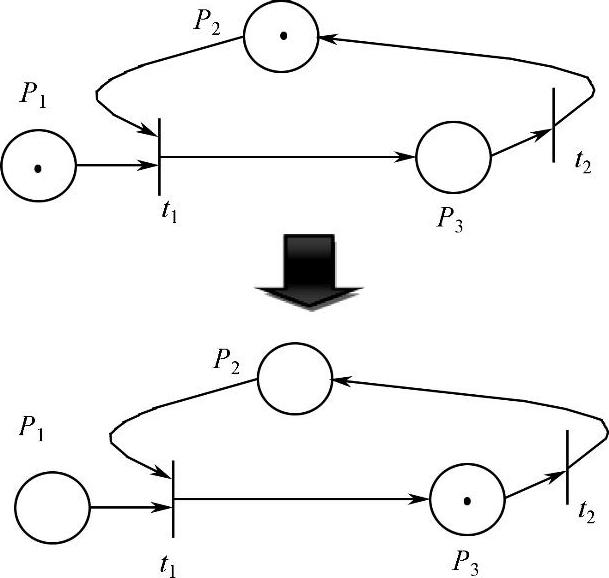
图4-2 变迁激发后的托肯变化

由此可知Petri网的托肯数并不是固定不变的，它与网的结构和输入函数，输出函数的权值等有关，其数目可根据公式m（p）=m（p）-I（p，t）+O（p，t）计算得出。

Petri网中的库所和变迁除了可以设为离散型，也可以设为连续型，但在表示结构图时，连续库所会用一个双实线圆表示，连续变迁会用黑实线或是双实线矩形表示。此部分会在下一节的混杂Petri网中重点介绍。

目前，随着连锁零售企业供应链网络规模的不断扩大和联网程度的不断增强，虽然一方面可以提高供货的可靠性与服务质量，但同时也带来了潜在的危险。为了降低或避免事故所带来的影响，需要及时检测连锁零售企业供应链可能面临的各种风险与故障，快速、准确地分类风险。同时，连锁零售企业供应链的大力发展，也迫切地要求及时发现、准确诊断并消除风险隐患，提升整个系统的安全可靠性。因此，研究和建立起一套高效的连锁零售企业供应链风险智能诊断系统，对于及时认知连锁零售企业供应链中设备风险，处理连锁零售企业供应链风险是十分必要的。目前该领域开展了不少研究工作，但警报信息丢失、虚假信息或信号不完备等现场不可避免的因素使风险故障诊断结果的准确性难以保证，阻碍了连锁零售企业供应链风险诊断方法的实用化。Petri网方法可以清晰、直观、准确地描述和研究网络中各个组成部件在故障状态下的离散动态行为，具有良好的容错性。此外随着Petri网的广泛应用，众多专家学者又进一步研究了模糊Petri网，它更符合人类的思维和认知方式。