遗传算法（GA）不同于传统的搜索与优化方法，它是随着问题种类的不同以及问题规模的扩大，能以有限的代价来很好地解决搜索和优化的方法。遗传算法作为一种借鉴生物进化规律的全优化随机搜索算法，具有内在的并行性和良好的全局寻优能力，其采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定的规则，对全局优化和复杂非线性的优化求解问题适应性很强。

本文采用基于代沟信息的遗传算法对岭回归参数进行优化，使种群保持良好的可进化性和收敛性。选用既能克服系统病态性又能抑制噪声和误差传播的正则化方法对岭回归算法参数进行优化，构造的适应度函数为

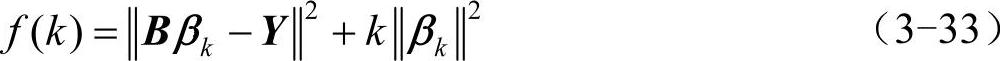
寻找使适应度泛函取极小值时参数k值。

优化岭参数的基本步骤如下：

1）确定一个适应度函数，明确k值变化范围，采用二进制进行编码；

2）设定种群大小、进化代数、交叉、变异概率和代沟等运行参数；

3）随机产生初始种群；

4）依据当前设定的岭参数k，计算岭估计参数β_k，适应度函数f（k）；

5）通过选择算子、交叉算子和变异算子，进行代数更迭；

6）求解新个体的适应度函数；

7）代数更新，如不满足终止条件继续5）。

通过确定岭参数k值，可以进一步求解出GM（2，1）白化方程的系数，建立预测模型。系统预测流程如图3-10所示。

应用GM（2，1）预测模型获得的预测序列应与原始数据序列进行比较，计算相对误差、平均误差、关联度来判断预测模型的使用效果。一般情况下，平均误差越小，关联度越大，模型越好，实际应用中，关联度大于0.6即可达到满意。

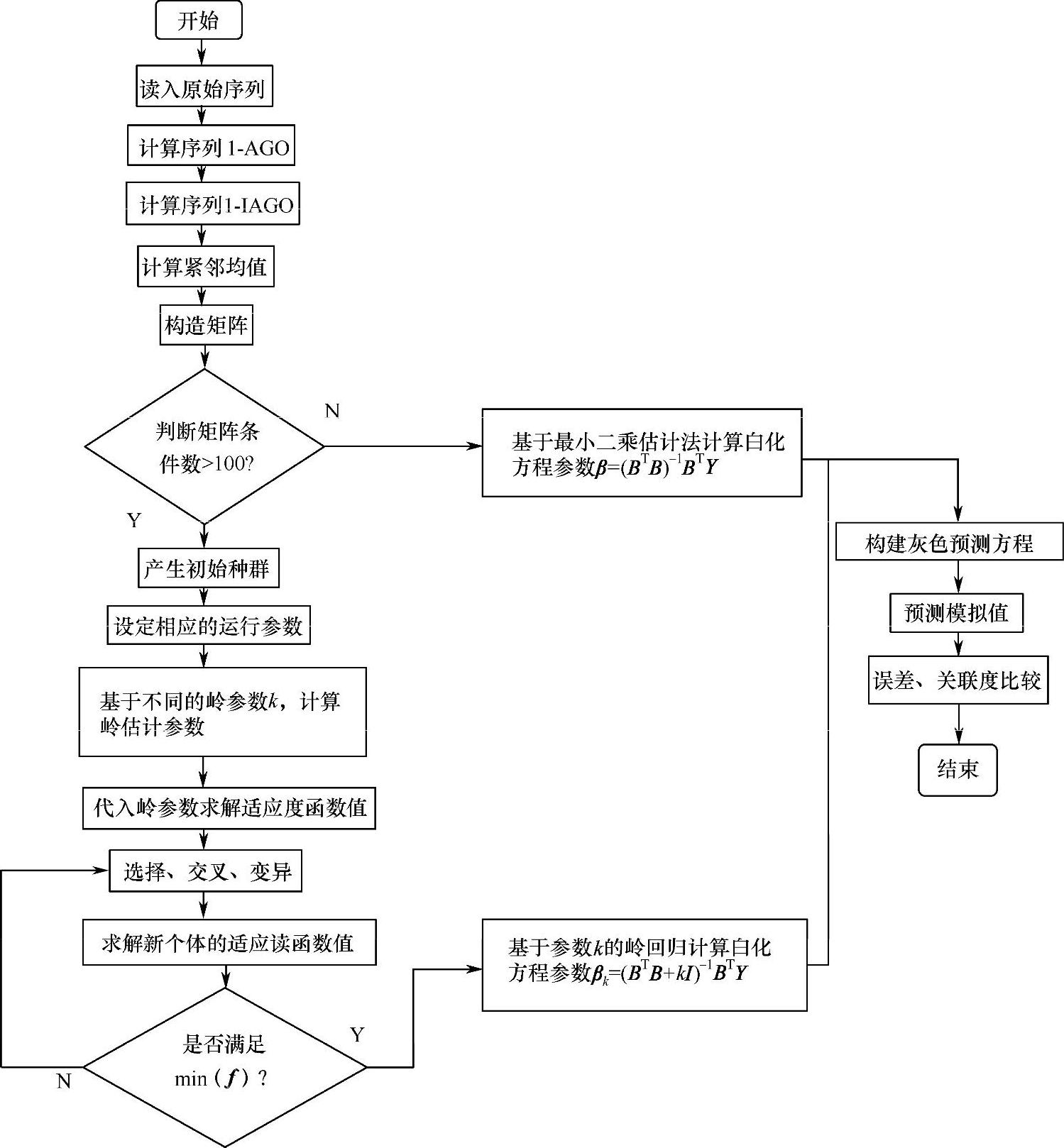
图3-10 遗传算法优化灰色岭回归流程

算例1：为便于分析，本文首先采用刘思峰教授著作中GM（2，1）模型例题数据用于优化研究，数据详见表3-4。

表3-4 GM（2，1）模型算例数据

通过本文提出的遗传算法确定岭参数k为20.1194，因此建立的优化岭回归GM（2，1）模型的最小二乘估计参数为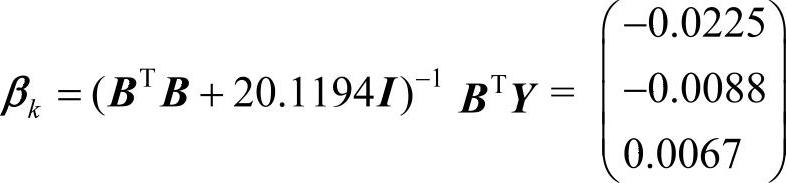，进一步通过累减获得数据列为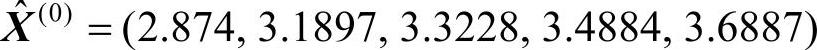，将与刘思峰算例记为1、刘圣保算例记为2中获取的数据列进行比较，得表3-5～表3-7。(www.daowen.com)

表3-5 典型数据序列分析比较表

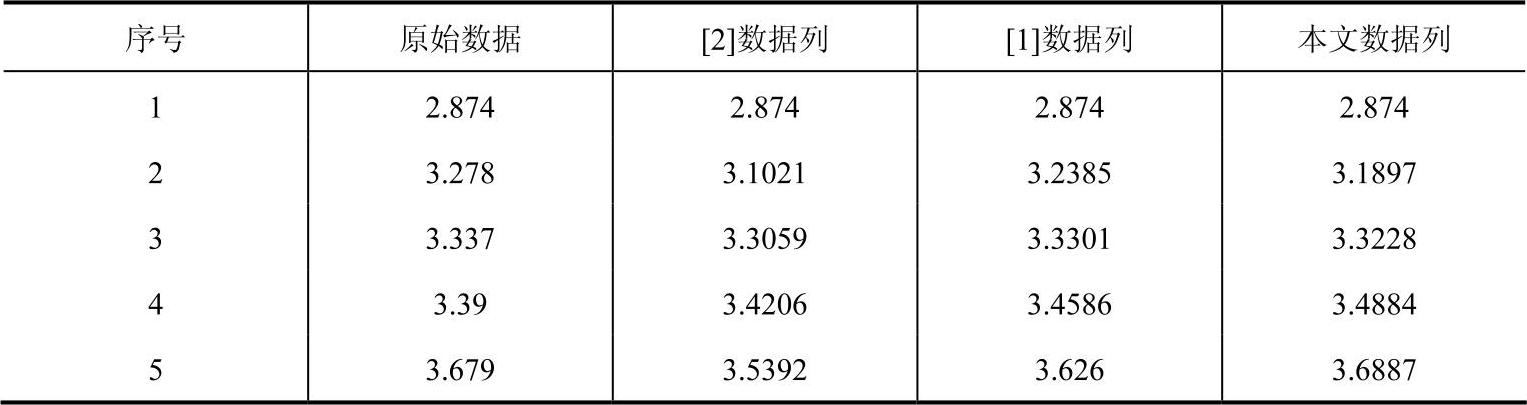
表3-6 典型数据误差比较表

表3-7 典型数据灰色关联度比较表

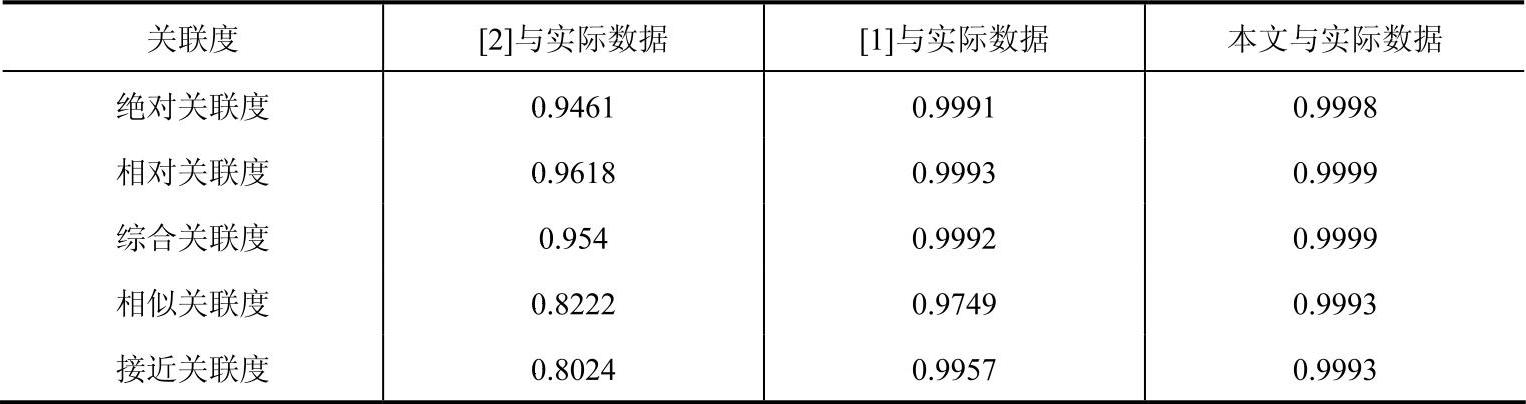
通过这些数据分析表易知采用本文提出优化预测算法，可使预测值较好地逼近实际值，体现出预测数据曲线的发展与实际情况相逐步接近的态势，在关联度分析中显示出一定的优势。采用遗传算法的优化灰色岭回归GM（2，1）预测模型，有效地解决了岭回归算法中岭参数难以确定的瓶颈，避免了病态方程引起的参数估计不准确的问题，且该算法，操作简便、易于理解、运算更具有客观性。

算例2：连锁零售企业配送环节的风险对系统的稳定运行具有重要意义，本算例2依据某连锁零售企业2002～2008年配送环节专家风险评价打分表，将10位专家打分后得到的数据进行均值处理，得到表3-8数据，其中风险值代表的风险程度含义见表3-9。

表3-8 2002～2008年专家评判风险值

表3-9 打分值及其对应区间

由于获取的数据离散度大，规律性差，这里先将风险值扩大百倍后再取对数，即X′=lnX，得到：X′=[3.7887 3.8733 3.8911 3.9759 3.8111 3.9140 3.7377]，将原序列转化为波动不大，数值较接近的数据序列。将该数据作为灰色预测模型的输入数据，采用遗传算法进行优化后确定岭参数k值为149.846。进一步获得预测数据序列为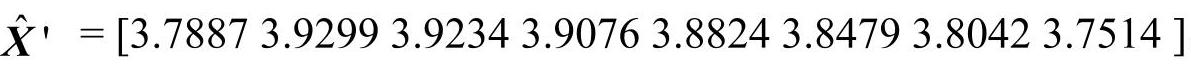，反变换后的风险值数据为 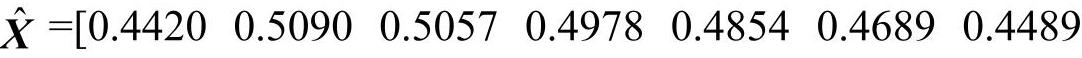0.4258]。与表3.8中的风险评判数据进行误差及关联度分析，数据列表见表3-10、表3-11。

表3-10 配送环节风险值误差分析

表3-11 配送环节风险值灰色关联度分析

可见风险预测值与实际专家给出风险值的关联度在0.97以上，相对误差控制在8%以内，之所以相对于算例1而言相对误差数值增大，这主要是由于配送环节中风险值中含有较多的扰动噪声。该算法可由计算机按程序直接计算，操作简便、易于理解，运算过程更具有客观性，对于非单调的波动型风险值的预测，采用GM（2，1）模型的预测结果与系统实际风险数据匹配的一致性较好，采用本算法对连锁零售企业配送环节风险进行预测可促使连锁零售企业管理者提前防范，规避风险。

本文为解决连锁零售企业风险预测所面临的风险数据少且含有不确定性扰动，系统运行呈现非单调的波动模态这一现实问题，建立GM（2，1）灰色预测模型。为改善参数求解过程中由于数据累加或累减产生的非线性问题，引入岭回归算法，并提出用遗传算法寻优确定岭参数k。算例分析结果表明，采用遗传算法优化基于岭回归的灰色GM（2，1）预测模型，方法原理简单、易于理解，预测效果可靠有效、误差较小。针对连锁零售企业供应链风险数据量小、扰动强、波动性大的特点，可以方便地预测出与实际系统运行相一致的风险发展趋势。