偏最小二乘回归方法是一种新型的多元统计数据分析方法，它最早由S.Wold和C.Albano等人于1983年提出的；在国内，最早对此进行系统研究的学者是北京航空航天大学的王惠文教授。

偏最小二乘回归法（Partial Least Squares Regression，PLSR）：是一种新型的多元统计数据分析方法，它主要研究的是多因变量对多自变量的回归建模，特别当各变量内部高度线性相关时，用偏最小二乘回归法更有效。另外，偏最小二乘回归较好地解决了样本个数少于变量个数等问题。偏最小二乘法是集主成分分析、典型相关分析和多元线性回归分析三种分析方法的优点于一身。它与主成分分析法都试图提取出反映数据变异的最大信息，但主成分分析法只考虑一个自变量矩阵，而偏最小二乘法还有一个“响应”矩阵，因此具有预测功能。

偏最小二乘回归分析方法的一个突出特点是它将多元线性回归分析、变量的主成分分析和变量间的典型相关分析有机地结合起来，在一个算法下同时实现了回归建模、数据简化和两组变量间的相关分析。

设有因变量y及自变量集合X=（x₁，…，x_p），偏最小二乘回归分析的算法步骤是，首先在X提取一个主成分t₁，它应尽可能地概括X中的信息，并与y的相关度最高；接着分别作X与y关于t₁的线性回归，若回归方程达到满意的精度，则停止算法；否则利用X被t₁解释后的残余信息以及y被t₁解释后的残余信息进行第二主成分t₂的提取，继续实施y和对X对t₁，t₂的回归。如此反复，直到达到一个满意的精度为止。若最终对X共提取了m个成分t₁，t₂，…，t_m（m≤n），偏最小二乘回归将施行y对t₁，t₂，…，t_m的回归，由于t₁，t₂，…，t_m都是x₁，x₂，…，x_k的线性组合，最后可以表达成y对原变量X的回归方程。

偏最小二乘回归分析在处理样本容量小、自变量多、变量间存在严重相关性问题方面有独特的优势，张恒喜等（2002）在其专著中有具体论述。目前，Rosipal R和TrejoL.J（2001）提出偏最小二乘回归与Kernel核技术相结合，出现了基于核的偏最小二乘方法，成为偏最小二乘回归分析的最热研究方向。

方差分量线性模型，在对小样本数据进行分析时，常会遇到样本的绝对数目较多，但样本之间存在明显的聚类倾向的情况，具体到每一类型之中，样本的容量又很小。对于这种形式的小样本问题，如果采用普通的多元回归分析方法，就会使模型的残差方差很大，这时可以通过建立一个混合的线性模型改善，即通过方差分析建立方差分量模型来研究。

对于一个线性模型，建立起矩阵形式：y=Xb+e，其方差分量模型的形式可以表示为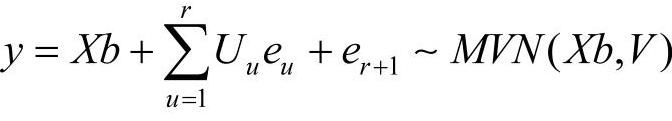：。式中，U_u为第u项随机因素e_u的系数矩阵；e_u和e_r+1有多元正态分布，即e_u∼MVN（0，σ²_uI），e_r+1∼MVN（0，σ²_r+1I）；V为协方差矩阵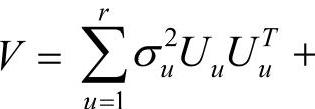，σ²_r+1I。

张文专等人（2006）研究指出随机效应是方差分量模型中的重要概念，残差效应也是一种随机效应。一个模型中，如果不考虑各因素之间的随机效应，就会引起残差方差的显著增长，方差分量模型就是要把这种随机效应分离出来并加以估计。运用方差分量模型进行预测时，对于一个新的样本，要先判别其属于样本中的哪一类型，如果不能将其归类，则不适合运用方差分量模型来估算。

可见，偏最小二乘回归（PLS）建模既能处理小样本高维数据，同时又能解决自变量之间的相关性问题，它打破了传统的时间与风险因素之间单输入单输出固定思维模式，独辟蹊径，根据环境变量、时间与风险因素、风险程度之间的关系，建立多输入多输出模型。

偏最小二乘回归的计算方法介绍：

假设有p个变量x₁，x₂，…，x_p，对他们分别进行了n次采样，得到n个样本点

（x_i1，x_i2，⋅⋅⋅x_ip），i=1，2，⋅⋅⋅，n

所构成的数据表可以写成n×p维的矩阵，X=[x₁，…，x_p]_n×p，在数据表中，x_j=（x_1j，x₂j，⋅⋅⋅，x_nj）′，j=1，2，⋅⋅⋅，p，它通常被称为变量。在数据表X中，表示所有样本点组成在j指标上的取值分布。

将X经过处理后的数据矩阵记为E₀=（E₀₁，⋅⋅⋅，E_0p）_n×p，Y经过处理后的数据矩阵记为F₀=（F₀₁，⋅⋅⋅，F_0q）_n×q。

第一步记t₁是E₀的第一个成分，t₁=E₀w₁，w₁是E₀的第一个轴，它是一个单位向量，即w₁=1。

记u₁是F₀的第一个成分，u₁=F₀c₁，c₁是F₀的第一个轴，它是一个单位向量，即c₁=1。

如果要t₁和u₁能很好地代表X和Y中的数据变异信息，那么

Var（t₁）→max

Var（u₁）→max

另一方面，由于建模的需要，要求t₁对u₁有最大的解释能力，也就算是说t₁与u₁的相关程度达到最大值。

综合以上信息，在偏最小二乘回归中，就是要求t₁和u₁的协方差达到最大，即

正规的数学表达式是求解下列优化问题：

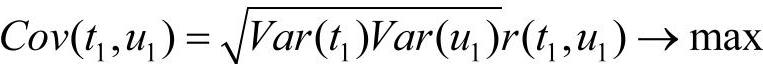
后续类似，用残差矩阵E₁、F₁取代E₀、F₀，然后求第二个轴w₂、c₂以及第二个成分t₂、u₂。(www.daowen.com)

如此计算下去，如果X的秩是A，则会有

E₀=t₁p₁′+⋅⋅⋅+t_Ap_A′ （3-24）

F₀=t₁r₁′+⋅⋅⋅+t_Ar_A′+F_A （3-25）

在现有的数据表下，提取的主成分越多，回归方程的精度就越高，但是样本点的扰动是不可避免的，即更高精度的回归方程的建立是以包含更多的样本点扰动误差为代价的。为了建立更精准的回归方程，必须确定提取主成分的最佳数目，而交叉有效性是解决这个问题的方法。

在偏最小二乘中，究竟选多少个成分为宜，可以通过考察增加一个新的成分后，能否明显地改善模型的预测功能来决定。采用类似于抽样测试法的工作方法，把n个样本点分成两部分：第一部分是除去某个样本点i的所有样本点集合（n-1个样本点），这部分样本点用h个成分拟合一个回归方程；第二部分是把刚才被排除的样本点i代入前面的拟合方程，得到y_j在样本点i上的拟合值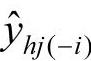，对于每一个i=1，2，…，n，重复上述测试，则可以定义y_i的预测误差平方和为PRESS_hj，有

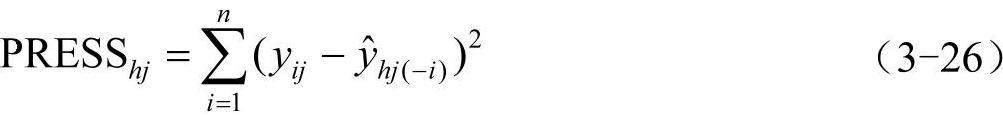
定义Y的预测误差平方和为PRESS_h，有

显然，如果回归方程的稳健性不好，误差很大，它对样本点的变动就会十分敏感，这种扰动误差的作用，就会加大PRESS_h值。

另外，再采用所有的样本点，拟合含h个成分的回归方程。这时，记第i个样本点的预测值为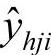，则可以定义y_j的误差平方和为SS_hj，有

定义Y的预测误差平方和为SS_h，有

一般情况下，总有PRESS_h大于SS_h，而SS_h则总是小于SS_h-1。下面比较SS_h-1和PRESS_h。SS_h-1是用全部的样本点拟合的具有h-1个成分的方程的拟合误差；PRESS_h增加了一个成分t_h，但却含有样本点的扰动误差。如果h个成分的回归方程的含扰动误差能在一定程度上小于（h-1）个成分的回归方程的拟合误差，就认为增加一个成分t_h会使预测的精度明显提高。因此，PRESSh/SSh_-1越小越好。

交叉有效性的定义如下，对于每一个因变量y_k，定义：

对于全部应变量Y，成分t_h的交叉有效性定义为

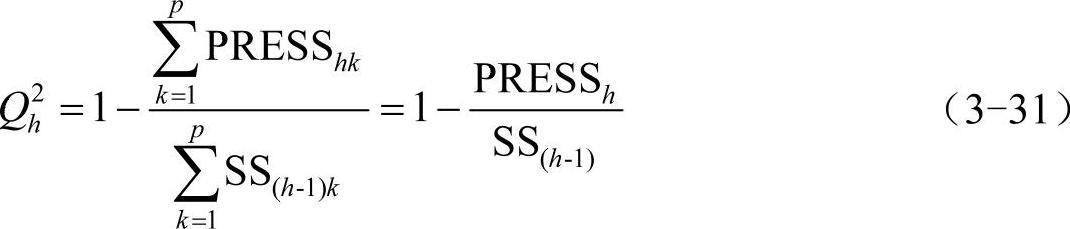
用交叉有效性测试成分t_h对预测模型精度的边际贡献有两个尺度：

1）当Q²_h≥0.0975时，t_h成分的边际贡献是显著的。

2）对于k=1，2，…，q，至少有一个k，使得Q²_kh≥0.0975，这时增加一个成分t_h，至少使一个因变量y_k的预测模型得到显著的改善，因此也可以考虑增加成分t_h。

偏最小二乘回归建模主程序流程如图3-9所示。

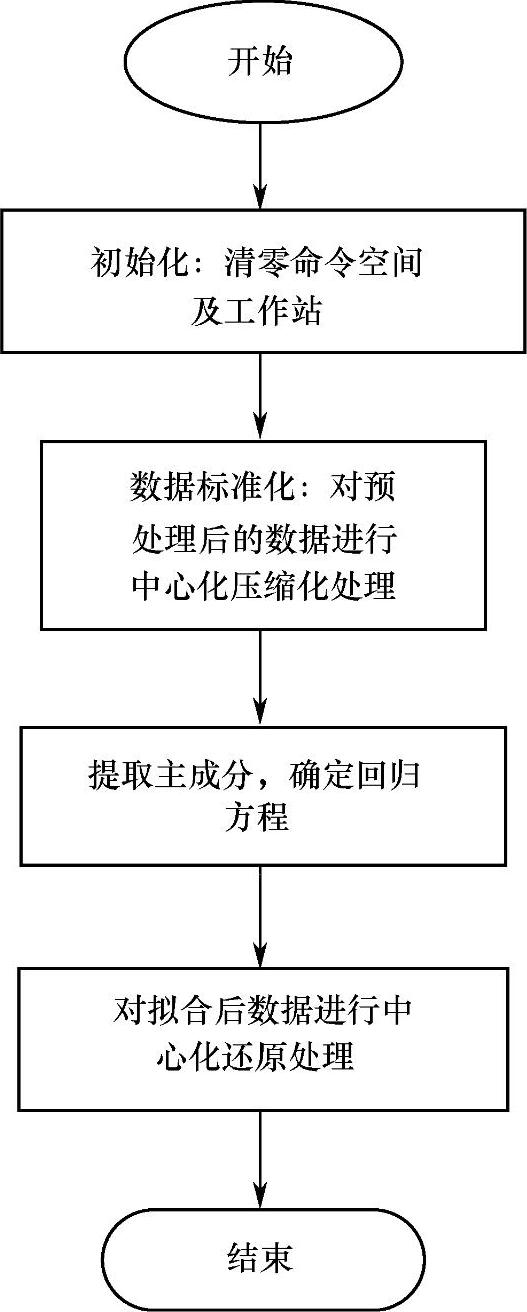
图3-9 偏最小二乘主程序流程图