贝叶斯预测模型是运用贝叶斯统计进行的一种预测。贝叶斯统计不同于一般的统计方法，其不仅利用模型信息和数据信息，而且充分利用先验信息。为了更好地理解贝叶斯预测模型，我们首先回顾一下贝叶斯定理：

设A₁和B表示在一个样本空间中的两个事件，给定B下A₁发生的条件概率公式为

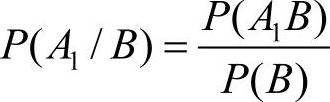
则A₁和B的联合概率公式为

P（A₁B）=P（A₁）P（B/A₁）

贝叶斯定理：假定存在一个完整的和互斥的事件A₁，A₂，…，A_n，A_i中的某一个出现是事件B发生的必要条件，那么n个事件的贝叶斯公式为

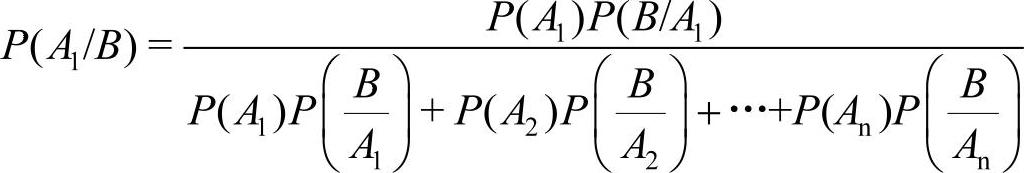
近年来，随着MCMC（Markov chain Monte Carlo，马尔可夫链蒙特卡尔理论）的深入研究，贝叶斯（T.Bayes（1702—1761））方法已成为当今国际统计科学研究的热点。翻阅近几年国内外统计学方面的杂志，特别是美国统计学会的JASA（Journal of the American Statistical Association）、英国皇家学会的统计杂志JRSS（Journal of the RoyalStatistical Society）等，几乎每期都有“贝叶斯方法”的论文。贝叶斯预测的应用范围很广，如勘探专家所采用的概率推理、计量经济中的贝叶斯推断、经济理论中的贝叶斯模型等。

最早，Silvert（1965）采用贝叶斯法来预测需求，首先统计需求量出现频率得到先验概率分布，然后在得到提前期的需求后，计算后验概率得到需求的后验分布，在满足缺货概率约束下根据需求分布来确定再订货点和订货批量。但该方法需要较大样本容量，而且各种可能的需求量值必须在样本中出现过。著名的美国统计学家Zellner（1987）教授研究了计量经济学中的贝叶斯理论，包括回归模型、完全递归模型和分布滞后模型的贝叶斯方法研究；美国学者Litterman（1986）利用贝叶斯方法，对明尼苏达州的生产总值等七个指标进行预测，并取得了很好的效果；此后，贝叶斯方法在商业经济预测和政府宏观经济预测的研究逐年增多。

基于贝叶斯方法的需求预测分析是统计学中具有重要理论意义和实用价值的国际上发展比较成熟的课题，与传统方法相比，它允许合理的利用先验信息，能更明确合理的处理不确定因素。贝叶斯方法考虑了市场需求先验信息和专家信息，其估计结果往往更合理，更能反映市场的实际需求状况，提高了预测的准确性，该方法还极大地增强了系统的灵活性。因此，本节将探讨运用贝叶斯分析的理论来预测市场的需求。

贝叶斯预测就是运用贝叶斯统计方法进行的一种预测，包括许多传统的预测方法，例如线性回归、指数平滑和线性时间序列模型，它们都是贝叶斯动态模型和预测的特殊情况。贝叶斯预测不仅利用过去的数据信息，还包括人的因素，人对预测负有责任并提供信息。它按照例外管理原则进行预测，这是贝叶斯预测的一个重要基本思想。贝叶斯预测利用客观信息和主观信息相结合的方法进行预测，它能处理异常情况的发生。这一特点尤其适用于动态测量。

托马斯·贝叶斯（Thomas Bayes）的统计预测方法是一种以动态模型为研究对象的时间序列预测方法。在做统计推断时，一般模式为

先验信息+总体分布信息+样本信息→后验分布信息

可以看出贝叶斯模型不仅利用了前期的数据信息，还加入了决策者的经验和判断等信息，并将客观因素和主观因素结合起来，对异常情况的发生具有较多的灵活性。

贝叶斯方法有如下特点：

1）经典统计方法在进行推断时，依据两类信息：一是模型信息，即统计总体服从何种概率分布，这是制定统计方法的基础；另一个是样本信息，即观察或实验的结果。贝叶斯方法则除了以上两类信息外，还利用另外一类信息，即总体分布中未知参数的分布信息。

2）贝叶斯统计方法是一个“从有到有的过程”：先验分布反映了实验前对参数分布的认识，在获得样本信息后，人们对这个认识有了改变，其结果就反映在后验分布中，即后验分布综合了参数先验分布和样本信息。

3）贝叶斯方法只能基于参数的后验分布来分析问题。也就是说，在获得后验分布后，如果把样本、原来的统计模型（包括总体分布和先验分布）都丢掉，也不会影响将来的统计推断问题。

贝叶斯理论实质上描述了一个如何利用采样信息修正和改进现有的概率分布的规律，本质上它概括了大多数成人的学习过程。贝叶斯理论常常被用于一个或者多个参数的估计，它有两个与传统的统计学不同的观点：

1）贝叶斯理论将待估计的参数ω看作是随机变量，而传统的统计学将ω看作是未知常数；

2）待估计参数ω在采样前就已经具有了先验分布π（ω）。

总体信息即总体分布或总体所属分布族给我们的信息。若已知总体是正态分布，我们就知道它的密度函数是一条钟形曲线，它的一阶矩都存在，有关服从正态分布的随机变量的某些事件的概率可以计算，并且由正态分布可以导出χ²分布、t分布和F分布等重要分布，还有许多成熟的点估计、区间估计和假设检验方法可供我们选用。

总体信息是很重要且很难得的信息，获得总体信息的过程通常历时长久、耗资巨大。例如茆诗松（2005）专著中提及要获得某种新的电子元器件的寿命分布，常常需要购买成千上万的此种元器件，做大量的寿命实验、获得大量数据后才能确认其寿命分布是什么。我国为确认国产轴承寿命分布服从两参数威布尔分布前后也花了五年时间，处理几千个数据后才定下来的。

样本信息是通过样本而给我们提供的有关信息。这类“信息”是最具价值和与实际联系最紧密的信息。人们总是希望这类信息越多越好。样本信息越多一般对总体推断越准确。

基于以上两种信息所做出的统计推断被称为经典统计。其特征主要是，把样本数据看成是来自具有一定概率分布的总体，所研究的对象是总体，而不是立足于数据本身。而除了以上两种信息，还有一种信息可以应用到统计推断中，那就是先验信息。

先验信息即在抽样之前有关统计问题的一些信息，它是总体分布参数θ的一个概率分布。贝叶斯学派的根本观点是，认为在关于θ的任何统计推断问题中，除了使用样本所提供的信息外，还必须对θ规定一个先验分布，它是在进行推断时不可或缺的一个要素。贝叶斯学派把先验分布解释为在抽样前就有的关于θ的先验信息的概率表述，先验分布不必有客观的依据，它可以部分地或完全地基于主观信念。

一般说来，先验信息主要来源于经验和历史资料。先验信息在日常生活中和工作中也经常可见，不少人在自觉或不自觉地使用它，但经典统计忽视了，对于统计推断是一个损失。

应用贝叶斯方法评定不确定度的关键是，在建立动态模型后确定先验分布，只有选择正确的先验分布，才能得出正确的后验分布，才能做出正确的统计推断。下面介绍一些常用的确定先验分布的方法。

1.用主观概率确定先验分布

一个事件的概率是人们根据经验对该事件发生的可能性所给出的个人信念，由此所得到的概率就是贝叶斯学派所称的主观概率。主观概率不是随意的，而是

要求当事人对所考察的事件有较透彻的了解和丰富的经验，甚至是这一行的专家，并能对周围信息和历史信息进行仔细分析，在这个基础上确定的主观概率才能符合实际。这正是我们需要的先验分布。

确定主观概率的常用方法如下：

1）用对立事件的比较确定主观概率，这是最简单的方法。假如对事件A与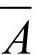说不出哪一个发生可能性大，就定P（A）=1/2，这个方法可以推广到多个事件。

2）用专家意见确定主观概率。当决策者对某事件了解不多时，可以征求专家意见，需要注意的是，对专家本人要较了解，以便做出适当的修正，形成自己的主观概率。

3）向多位专家咨询，并经过综合和修正获得主观概率。

4）充分利用已有的历史数据，帮助形成初步概念，然后做一些对比修正，再形成个人信念，以便给出主观概率。

根据经验和历史资料等先验信息给出主观概率没有固定的模式，还可以在实践中创造，但所确定的主观概率都必须符合概率的三条公理：

a）非负性公理：对任一事件0≤P（A）≤1；

b）正则性公理：必然事件的概率为1；

c）可列可加性公理：对可列互不相容的事件A₁，A₂，…有

2.利用先验信息确定先验分布

如果参数θ是连续的，要构造一个先验密度π（θ）就比较困难了。当总体参数是连续时，并且可以得到参数的足够信息（经验和历史数据等），可以用下面的方法确定先验分布：

（1）直方图法：把参数空间分成若干小区间，统计历史数据及经验确定每个小区间的主观概率或频率，画出频率直方图，在直方图上作一条曲线，尽量使曲线下的面积与直方图的面积相等，这条曲线就是π（θ）。

（2）确定先验密度函数形式再估计其超参数：根据先验信息选定θ的先验密度函数π（θ）的形式，当其中含有未知参数（超参数）时，如π（θ；α，β），给出α，β估计值使π（θ；α，β）最接近先验信息。

（3）定分度法与变分度法：定分度法是把参数可能取值的区间逐次分为相等的小区间，在每个小区间上请专家给出主观概率；变分度法是把参数可能取值的区间逐次分为机会相等的两个小区间，然后经过整理加工即可得到累积概率分布曲线。

3.无信息先验分布

没有先验信息可利用的情况下，如何确定先验分布，不少统计学家参与研究了这个问题，至今已提出多种无信息先验分布。

（1）贝叶斯假设：参数θ的无信息先验分布是指除参数θ的取值范围和参数θ在总体分布中的地位之外，再也不包含参数的任何信息的先验分布。不包含参数θ的任何信息是指对θ在取值范围内取任何可能值都相同，没有偏爱，都同样是无知的。

因此参数θ的先验分布选为均匀分布，即

式中，Θ为参数θ的取值范围；c为一个容易确定的常数。这一做法通常被称为贝叶斯假设。

对于参数θ是无限区间的情况，常选用π（θ）=1作为先验密度。贝叶斯统计学家为了把这种不正常的均匀分布纳入先验分布的行列，特地给出广义先验分布的概念。设总体X～f（x|θ），θ∈Θ若θ的先验密度π（θ）满足下列条件：

1）π（θ）≥0，且；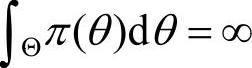

2）由此决定的后验密度π（θ|x）是正常的密度函数，则称π（θ）为θ的广义先验密度。

（2）位置参数的无信息先验分布：X具有下列形式的密度函数族称为位置参数族：

{f（x-θ）：-∞＜θ＜+∞，-∞＜x＜+∞}

式中，θ为位置参数，对于位置参数族，位置参数e的先验分布为

π（θ）∝1

后验分布可以看作是人们用总体信息和样本信息对先验分布作调整的结果。先验分布π（θ）是反映人们在抽样前对总体分布参数θ的认识，而后验分布π（θ|x）则是反映人们在抽样后对θ的认识。

根据样本X的分布及总体分布参数θ的先验分布π（θ），用概率论中求条件概率分布的方法，可算出在已知X=x的条件下，θ的条件分布π（θ|x）。因为这个分布是在抽样以后才得到的，故称为后验分布。贝叶斯学派认为：这个分布综合了样本X及先验分布π（θ）所提供的有关的信息。抽样的全部目的，就在于完成由先验分布到后验分布的转换。

贝叶斯公式的事件形式：设A₁，A₂，…，A₃是两两互斥的事件，且P（A₁）＞0，i=1，2，…，n，另有一事件B，它总是与A₁，A₂，…，A₃之一同时发生，则

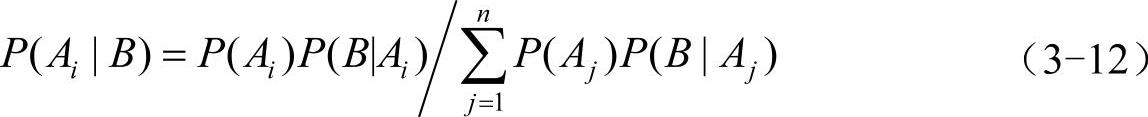
式中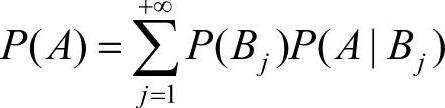，，即全概率公式。

特别有，设事件A、B为试验E的两事件，由于B和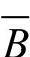是一个完备事件组，若P（A）＞0，P（B）＞0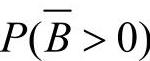，，贝叶斯公式的一种常用简单形式为

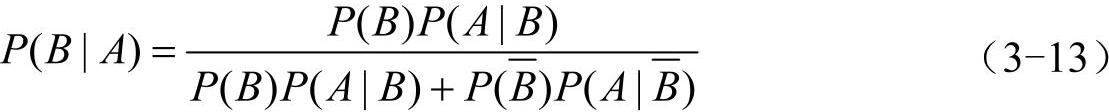
直观地将A_i看成是导致随机事件B发生的各种可能的原因，则P（A_i）可以理解为随机事件A_i发生的先验概率。如果我们知道随机事件B发生这个新信息，则它可以用于对事件A_i发生的概率进行重新的估计。事件P（A_i|B）就是知道了新信息“A发生”后对于概率的重新认识，称为随机事件A_i的后验概率。

贝叶斯公式的密度函数形式依赖于参数θ的密度函数在经典统计中记为P（x；θ），它表示在参数空间Θ={θ}中对应不同的分布。可在贝叶斯统计中记为P（x；θ），它表示在随机变量θ给定某个值时，总体指标X的分布。根据参数θ的先验信息确定先验分布π（θ）。这样一来，样本x和参数θ的联合分布为h（x，θ）=P（x|θ）π（θ），这个联合分布把样本信息、总体信息和先验信息都综合进去了。(www.daowen.com)

我们的任务是要对未知数θ作出统计推断。在没有样本信息时，人们只能据先验分布对θ作出推断。在有样本观察值x=（x₁，x₂，…，x_n）之后，我们应该依据h（x，θ）对θ做出推断。为此我们需把h（x，θ）作如下分解：

h（x，θ）=π（θ|x）m（x） （3-14）

式中，m（x）为x的边缘密度函数。

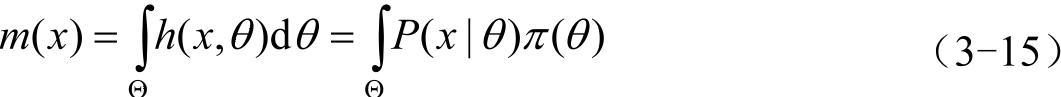
它与θ无关，或者说，m（x）中不含θ的任何信息。因此能用来对θ作出推断的仅有条件分布π（θ|x）。它的计算公式为

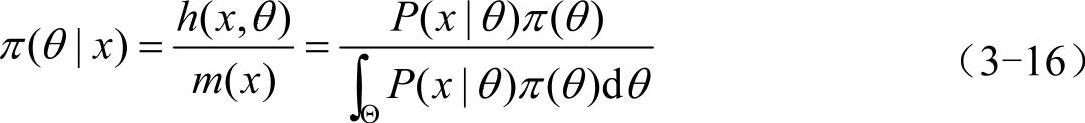
这就是贝叶斯公式的密度函数形式。这个在样本X给定下，θ的条件分布被称为θ的后验分布。它是集中了总体、样本和先验等三种信息中有关θ的一切信息，而又是排除一切与θ无关的信息之后所得到的结果。故基于后验分布π（θ|x）对θ进行统计推断是更为有效，也是最合理的。

例如经典统计学认为参数的无偏估计应满足：其中平均是对样本空间中所有可能出现的样本而求的，可实际中样本空间中绝大多数样本尚未出现过，而多数从未出现的样本也要参与平均是实际工作者难以理解的。故在贝叶斯推断中不用无偏性，而条件方法是容易被实际工作者理解和接受的。针对贝叶斯估计定义3.2使后验密度π（θ|x）达到最大的值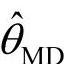称为最大后验估计；后验分布的中位数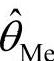称为后验中位数估计；后验分布的期望值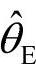称为θ的后验期望值估计，这三个估计都称为贝叶斯估计，记为。

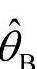例如为估计不合格率θ，今从一批产品中随机抽取n件，其中不合格品数X服从B（n，p），一般选取Be（α，β）为θ的先验分布，设α、β已知，由共轭先验分布可知，θ的后验分布为Be（α+x，β+n-x）。

可计算得

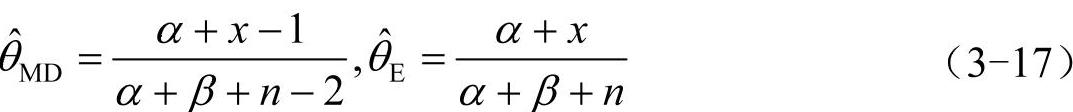
选用贝叶斯假设α=β=1，则

第一、在二项分布时，θ的最大后验估计就是经典统计中的极大似然估计，即θ的极大似然估计就是取特定的先验分布下的贝叶斯估计。

第二、θ的后验期望值估计θ要比最大后验估计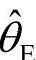更合适一些。

贝叶斯预测是针对随机变量未来观察值做出统计推断称为预测，譬如：设随机变量X～P（x|θ），在参数θ未知情况下如何对X的未来的观察值做出判断；设x₁，…，x_n是来自P（x|θ）的过去观察值，在参数θ未知的情况下，如何对X的未来的观察值作出推断；按密度函数P（x|θ）得到的一些数据x₁，…，x_n后，如何对具有密度函数g（z|θ）的随机变量Z的未来的观察值做出推断，这里两个密度函数P和g都含有相同的未知参数θ。

本文主要是应用贝叶斯理论中的预测部分，对市场需求进行分析预测。其主要方法是获得θ的先验分布π（θ）或后验分布π（θ|x），进而推断预测值或得出预测估计。主要有两种方法可得出先验或后验分布，如下所示。

设随机变量X～P（x|θ），在无X观察数据时，利用先验分布π（θ）容易获得未知的、但可观察的数据x的分布为

这个分布常数被称为X的边缘分布，又被人们称为先验预测分布，这里的预测是指对过去的数据没有要求。X是可观察量的分布，有此先验预测分布就可以从中提取有用信息，做出未来观察值的预测值或未来观察值的预测区间。

第二种情况：在有X的观察数据x=（x₁，…，x_n）时，利用后验分布π（θ|x）容易获得未知观察值的分布，如果预测同一总体P（x|θ）的未来观察值，则有

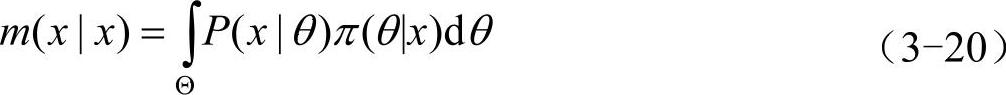
如要预测另一总体g（z|θ）的未来观察值，则有

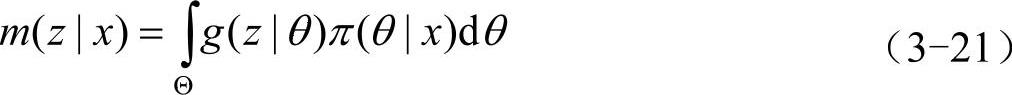
式中，m（x|x）和m（z|x）成为后验预测分布。

贝叶斯预测需要建立动态模型，所谓动态线性模型（Dynamic Linear Models，DLM）是由两个方程确定的系统，这个系统描述：过程的观测如何随机地依赖于当前的状态参数；状态参数如何随时间变化表示系统内部的动态变化和随机扰动。

观测方程：μ_t=μ_t-1+ω_t，ω_t～N[0，W_t]

状态方程：y_t=μ_t+υ_t，υ_t～N[0，V_t]

初始信息：µ₀|D₀～N[m₀，C₀]

其中，µ为t时刻序列的水平；v_t为观测误差项或噪声项；ω_t为状态误差项。

观察方程和系统方程中都有一个误差项，我们假定在每个时刻t，它们都服从正态分布；还假定在任何时刻t，两个误差序列本身都是独立的；并且对t≠s的所有t和s、v_t和v_s、ω_t和ω_s、v_t和ω_s都是独立的；更进一步假设，对于每个t，方差V_t和W_t都是已知的。

定理：对于每一时刻t，假设µ_t-1的后验分布（µ_t-1|D_t-1）～N[m_t-1，C_t-1]，则μ_t的先验分布（µ_t|D_t-1）～N[m_t-1，R_t]，其中R_t=C_t-1+W_t。

证明：由于μ_t=μ_t-1+ω，ν_t、ω_t和μ_t相互独立，故

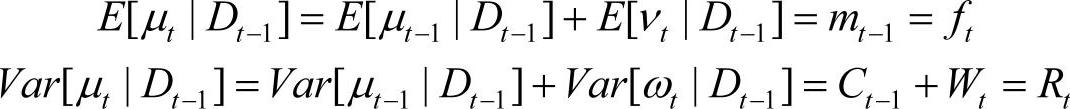
由正态分布的可加性可知（µ_t|D_t-1）～N[m_t-1，R_t]。

推论1：（y_t|D_t-1）～N[f_t，Q_t]，其中f_t=m_t-1，Q_t=R_t+V_t。

证明：由y_t=μ_t+υ_t，故有

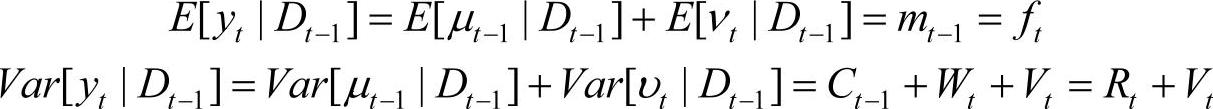
所以（y_t|D_t-1）～N[f_t，Q_t]。

推论2：µ_t的后验分布（µ_t|D_t）～N[m_t，C_t]，其中C^-1_t=R^-1_t+V^-1_t，m_t=C_t（R^-1_tm_t-1+V_t-1y_t）。若记A_t=R_tQ_t，e_t=y_t-f_t-1，则有m_t=m_t-1+A_te，C_t=A_tV_t。

证明：由上可知，µ_t与y_t的相关系数为

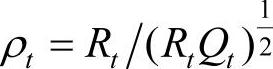
回归系数为A_t=（C_t-1+W_t）（C_t-1+W_t+V_t）=R_tQ_t=ρ²_t

由条件正态理论可知

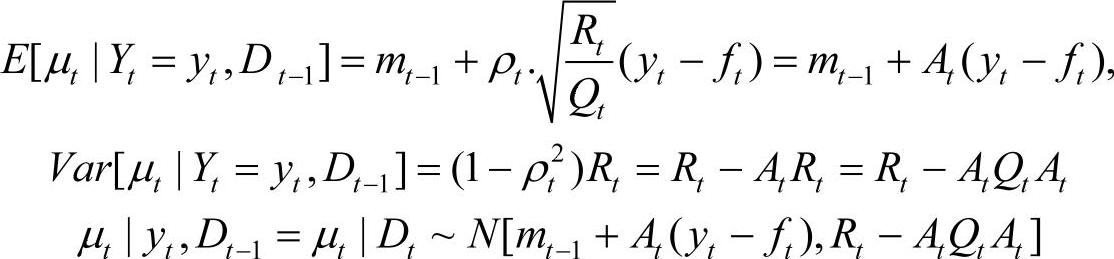
即µ_t|D_t～N[m_t，C_t]

其中m_t=m_t-1+A_t（y_t-f_t）=m_t-1+A_te_t，e_t=y_t-f_t

C_t=R_t-A_tQ_tA_t=R_tQ_t⋅（Q_t-R_t）=A_tV_t

其计算步骤为

①R_t=C_t-1δ；②Q_t=R_t+V_t；③A_t=R_tQ_t；④f_t-1=m_t-1；⑤e_t=y_t-f_t-1；⑥C_t=A_tV_t；⑦m_t=m_t-1+A_te。

一阶多项式（常数正态）折扣贝叶斯模型数值算例：为了检测一阶多项式（常数正态）折扣贝叶斯模型的实际效果，对美国出口额（见表3-2）的数据进行预测。

表3-2 1960～2005年美国货物出口额 （单位：十亿元）

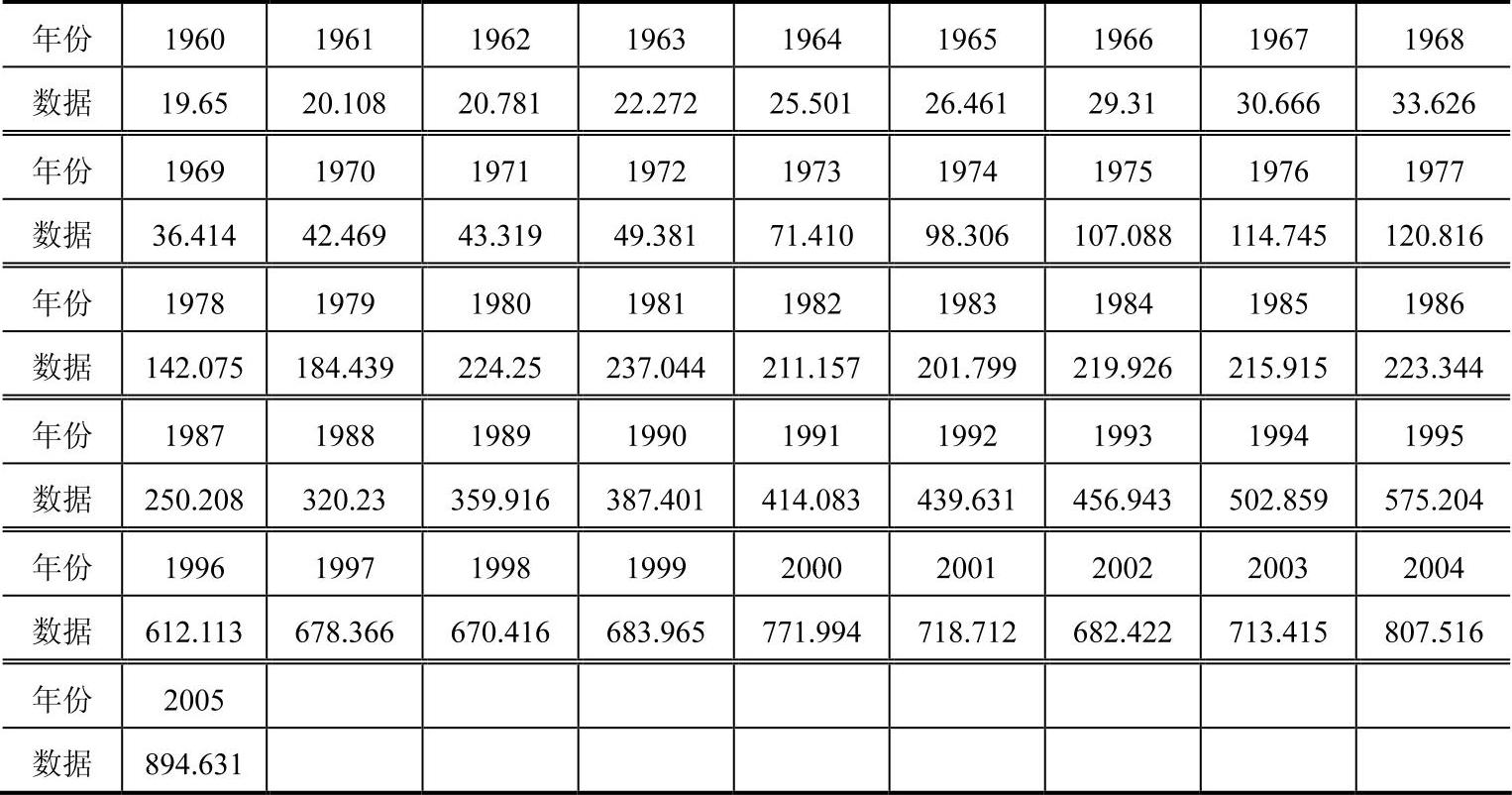
预测模型的初始信息为m₀=304，C₀=72，V₀=0.01，δ=0.8，现应用MATLAB软件进行预测，根据一阶多项式（常数正态）折扣贝叶斯模型绘制流程图，如图3-8所示。

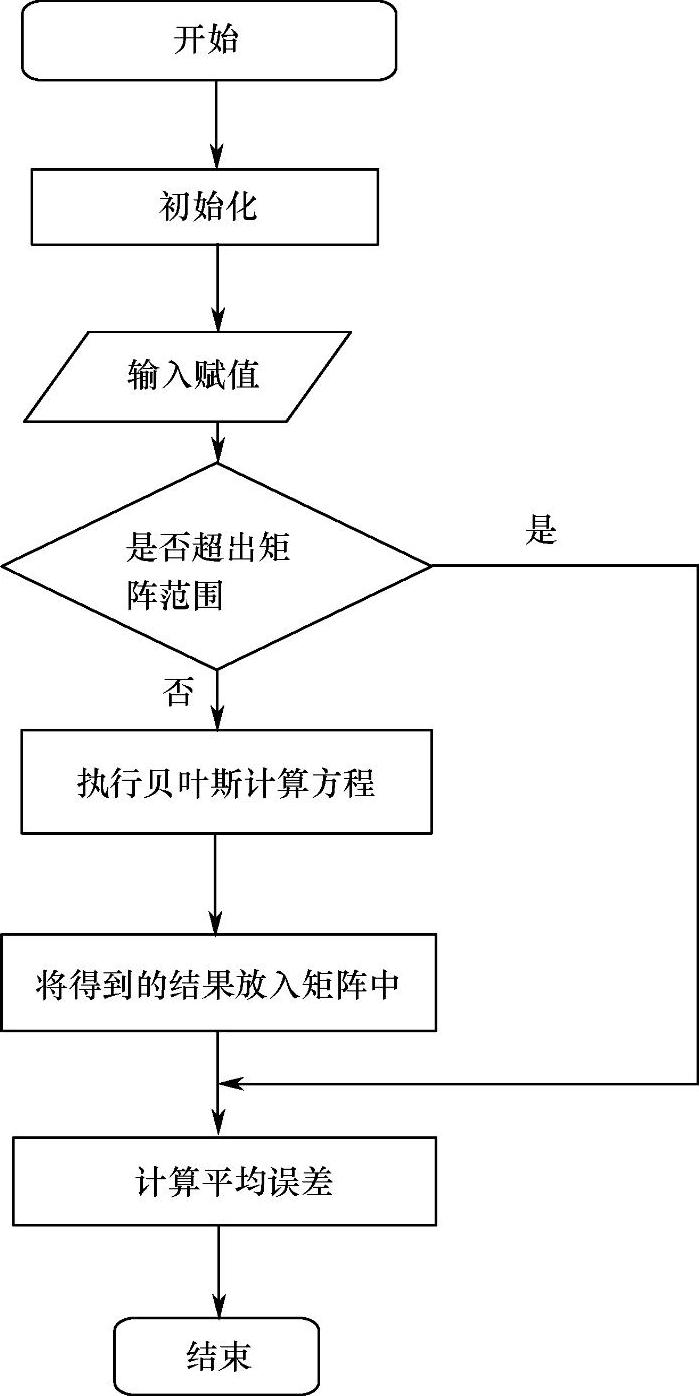
图3-8 一阶多项式（常数正态）折扣贝叶斯模型绘制流程图

整理得表3-3的一阶多项式（常数正态）折扣贝叶斯模型的计算结果数据。

表3-3 应用贝叶斯模型的出口额预测分布

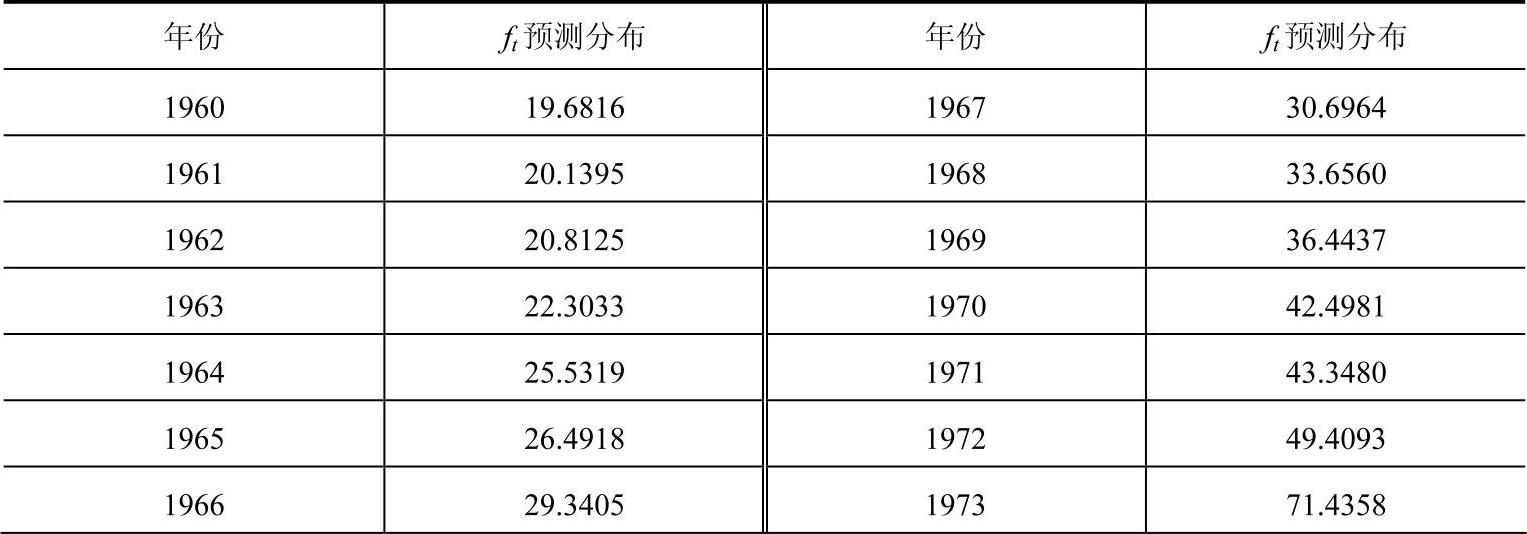
（续）

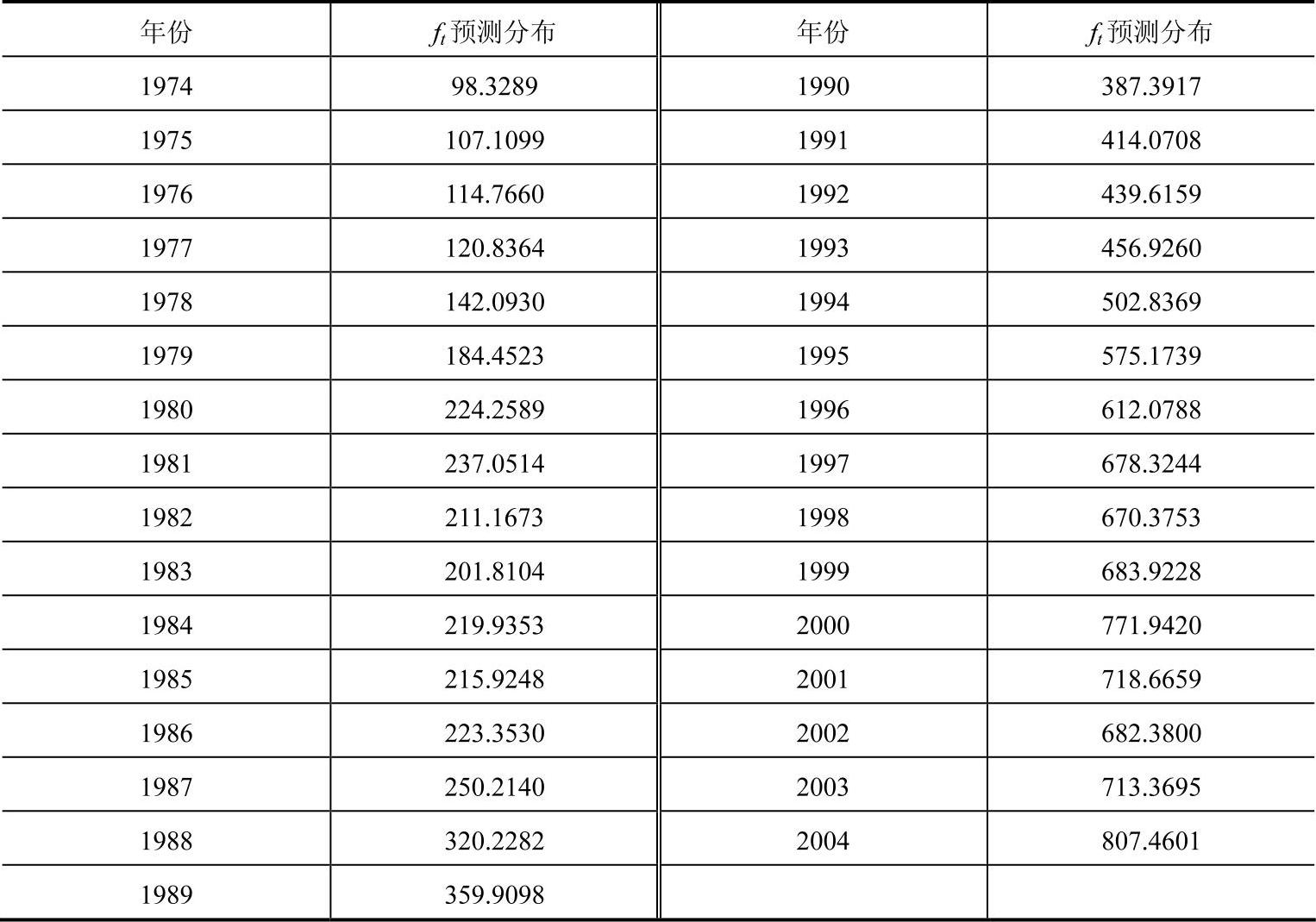
对预测结果进行平均绝对百分误差分析，公示如下：

根据预测出的1960年到2005年的出口额，运行MATLAB程序，得出阶多项式（常数正态）折扣贝叶斯模型的平均绝对百分误差为7.73%。

近年来，随着网络技术的不断发展，贝叶斯网络作为一种概率网络，用于表示变量之间的依赖关系，形成带有概率分布标注的有向无环图，能够图形化地表示一组变量间的联合概率分布。

在供应链质量风险管理的过程中，关键风险指标是适用于风险评估和监测的重要工具，所以供应链各企业往往设置一些关键的风险指标来评估和监控供应链质量风险。利用关键风险诱因和关键风险指标分析法，得出供应链质量风险的关键诱因和关键指标，在此基础上建立了贝叶斯网络结构模型，通过模型的应用表明了：在风险管理中，一些风险标指值的变化影响其他指值的变化，企业可以依据过往的经验设定各节点指标值的取值范围，从而定位导致风险产生的首要因素。所以本方法的应用有利于供应链风险动态的监控和管理。