网络系统的复杂程度体现，主要是通过调整网络内部大量节点之间相互连接的关系，从而达到处理信息的目的。人工神经网络是人工构建的一种借鉴人脑工作机制的网络，是一种应用类似于大脑神经突触连接的结构进行信息处理的数学模型。在工程与学术界也常直接简称“神经网络”或类神经网络。

人工神经网络（Artificial Neural Networks，ANNs）也简称神经网络（NNs）或称作连接模型（Connection Model），它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。1943年，心理学家W.S.McCulloch和数理逻辑学家W.Pitts建立了神经网络和数学模型，称为MP模型。他们通过MP模型提出神经元的形式化数学描述和网络结构方法，证明单个神经元能执行逻辑功能，从而开创人工神经网络研究的时代。大多数情况下人工神经网络能在外界信息的基础上改变内部结构，是一种自适应系统。现代神经网络作为一种非线性、统计性数据建模工具，常用来对输入和输出间复杂的关系进行建模，或用来探索数据的发展与结构模式。

人工神经网络作为一种运算模型，是由大量的节点（或称“神经元”，或“单元”）和节点之间相互连接构成。因此，人工神经网络技术发展离不开硬件基础与数学模型。近年来，随着人工智能科学研究的深入，人工神经网络在非线性建模与预测领域得到了广泛的应用，并取得了良好的效果。目前国内外的一些学者在预测复杂的非线性问题时，发现人工神经网络模型比一些传统建模方法具有更强的处理矛盾样本的能力，且预测精度比较高。

在实际应用中，面对一个具体的问题，首先需要分析一下如何利用神经网络确定预测问题的具体表达，然后依据问题特点，确定网络模型结构与参数。最后通过对神经网络进行学习、训练、仿真等，检验网络的预测性能是否满足要求。图3-1所示为采用神经网络进行预测研究的具体步骤。

图3-1 人工神经网络预测步骤框图

作为一种智能建模方法的主要分支，人工神经网络建模与预测算法有着自己的独特优势，如并行计算能力，具有较强的容错水准，更高的智能水平，更接近人的大脑，便于理解、简单方便等。

BP算法的学习由两种方法组成：信号的正向传播和误差的反向传播。输入样本正向传播通过输入层、隐层到达输出层。此时进行判断，若输出层的实际输出与教师信号不符，此时进行误差反传。当其网络输出误差减小到可接受的程度或到达预先设定的学习次数时，完成学习。采用BP网络预测能从多方面了解连锁零售企业供应链风险因素的交互影响，对供应链中运行状态进行监测、评估，考察主要风险因素对供应链中关键节点企业的配送时间、库存能力、顾客忠诚度与满意度等信息对其运行稳定性的影响，将这些状态信息量化作为BP网络的输入数据，可以预测其在异常情况出现时的潜在风险等级。图3-2所示为采用BP神经网络建立神经网络预测模型的流程图。

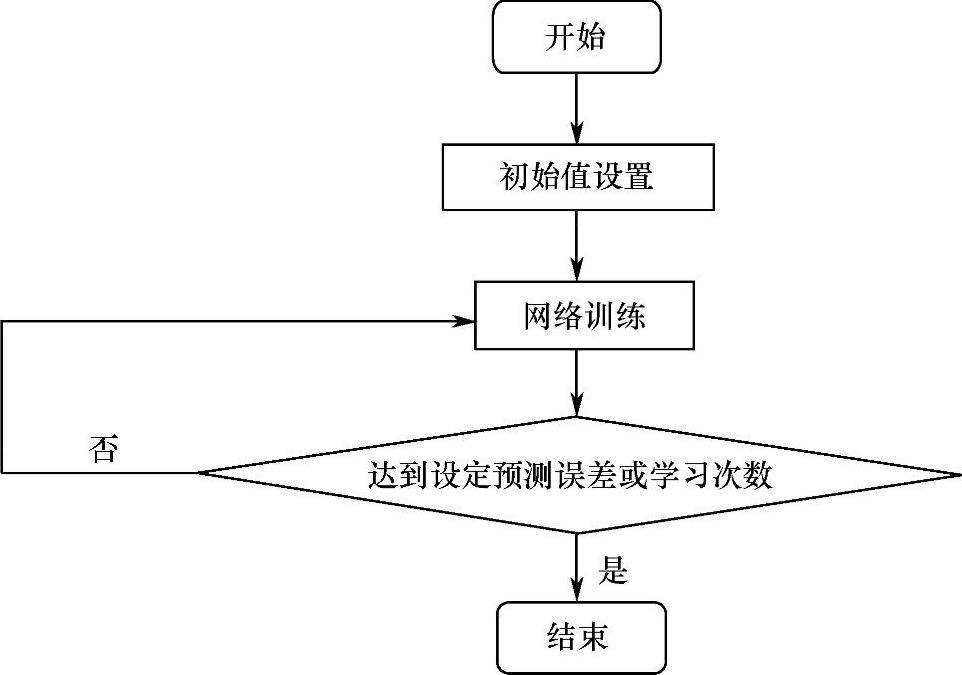
图3-2 神经网络建模与预测算法流程图

径向基函数（RBF，Radial Basis Function）方法。1985年，Powell提出了多变量插值的RBF方法，此后1988年，Broom和Lowe首先将RBF应用于神经网络设计，构成了RBF网络。径向基函数网络（即RBF网络）是一种前馈神经网络，一般是由输入层、隐含层和输出层构成的三层网络结构，如图3-3所示。

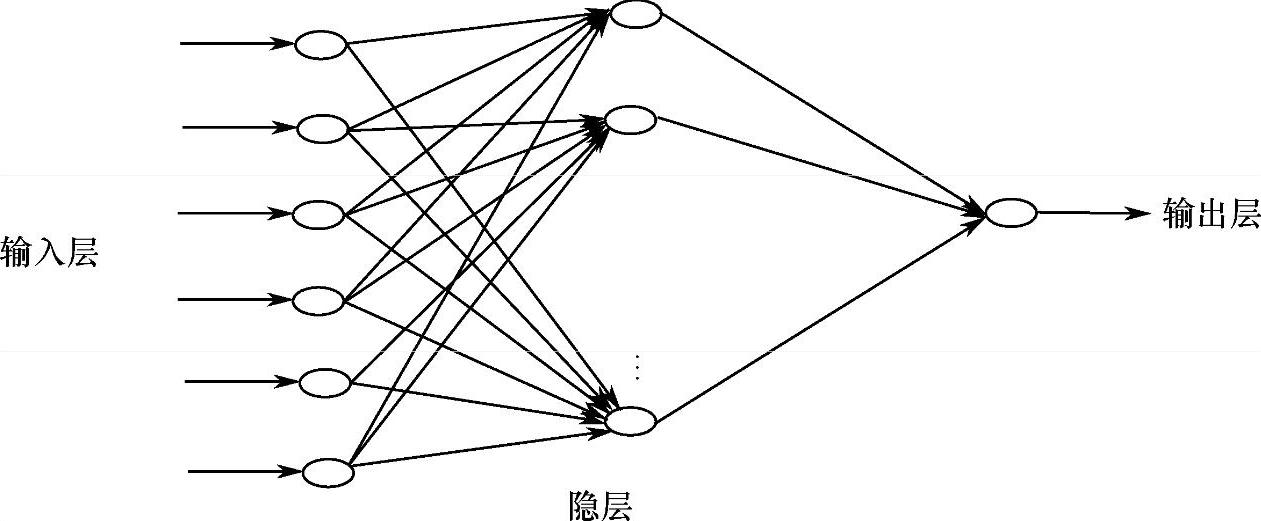
图3-3 RBF神经网络结构示意图(www.daowen.com)

由图易知，信号先由输入层传递到隐层，而后在由隐层传递到输出层。RBF神经网络的隐层结点函数一般为非线性高斯函数，而输出层一般为简单的线性函数。

RBF神经网络的工作原理为隐层神经元的网络输入为加权输入信号与相应阈值的乘积，然后通过神经元函数计算得到对应隐层神经元的网络输出。

颜刚等（2011）分析了基于RBF神经网络的导弹备件需求量预测仿真。针对导弹部署后期与备件有关的各项保障数据相对较多的情况，该文献采用了径向基神经网络建模方法。以某型号导弹的某备件为预测对象，对导弹维修备件需求影响因素进行分析。该方法比普通前向网络训练网络性能高，并且该方法在设计时，不需设计隐层，比普通前向网络训练更省时，能够高速并有效地解决备件需求量的预测问题。RBF神经网络用于预测与传统的BP网络模型相比，预测结果与精度更令人满意。通常RBF神经网络预测模型的收敛性也更好。

目前，神经网络存在的问题：收敛速度比较慢、易陷入局部极小、易导致网络瘫痪问题、不稳定性等。BP算法的改进主要包括：学习速率的改进、误差函数的改进、激励函数的改进、网络初始值的选取（使用Cauchy不等式和线性代数方法得到最优初始权值或采用遗传算法来初始化权值）、优化网络结构（关键是隐层的层数与隐节点的数目。隐节点过少，学习过程不可能收敛到全局最小点；隐节点过多，网络性能下降，节点冗余）、改进优化算法。

神经网络的设计要用到遗传算法，遗传算法在神经网络中的优化应用主要反映在：网络的学习、网络的结构设计、网络的分析三个方面。遗传算法可用于神经网络学习时，它在两个方面起作用：

（1）学习规则的优化：用遗传算法对神经网络学习规则实现自动优化，从而提高学习速率。

（2）网络权系数的优化：用遗传算法的全局优化及隐含并行性的特点提高权系数优化速度。

遗传算法在网络设计中的应用主要体现在用遗传算法解决网络结构的编码问题；然后才能以选择、交叉、变异操作得出最优结构。遗传算法在网络分析中的应用则是基于神经网络由于有分布存储等特点，一般难以从其拓扑结构直接理解其功能，而采用遗传算法可对神经网络进行功能分析，性质分析，状态分析，多方面地综合网络信息。

遗传算法和人工神经网络都是将生物学原理应用于科学研究的仿生学理论成果。尽管二者的产生都受到了自然界中信息处理方法的启发，但来源并不相同，G A是从自然界生物进化机制获得启示的，而ANN则是人脑或动物神经网络若干基本特性的抽象和模拟。因此，它们在信息处理时间上存在较大差异。近年来，已有越来越多的研究人员尝试着GA与ANN相结合的研究，希望通过结合充分利用两者的长处，寻找出一种有效地解决问题的方法，同时，也借助这种结合使得人们更好地理解学习与进化的相互作用关系。

罗长寿等（2011）分析研究了基于神经网络与遗传算法的蔬菜市场价格预测方法研究。该文献采用蔬菜市场价格数据，分别建立了BP神经网络模型、RBF神经网络模型以及基于遗传算法的神经网络模型，利用三种模型对2008—2009年蔬菜价格的预测进行对比讨论，并进行集成。研究表明三种模型预报结果的平均绝对误差分别为0.15%、0.144%、0.114%，遗传算法的神经网络模型对于数据的模拟稍差于BP神经网络模型，但是模型的泛化能力以及预报方面的能力要强于其他神经网络模型。

可见，基于遗传算法的神经网络模型可有效地避免遗传算法精度低，以及神经网络易陷入局部最优的缺点，能够实现参数的全局高精度优化。通常，基于遗传算法的神经网络的预测模型比单神经网络的预测模型预测精度高，可用于一些需要快速跟踪或预测的研究。