模糊综合评价法是一种基于模糊数学的综合评标方法。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价，即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。它具有结果清晰，系统性强的特点，能较好地解决模糊的、难以量化的问题，适合各种非确定性问题的解决。

供应链风险评估是对供应链风险的测量，评估的结果直接影响供应链风险管理的手段和方法。供应链风险评估主要是根据前面的风险识别，采用定量或定性的方法测量出供应链风险的大小，常用的风险评价方法有平衡点法、敏感性分析法、概率分析法等。目前，国内外文献对供应链风险评估的定量研究还非常少，总体来说，定量研究集中在供应链风险的测度和最优化风险决策上，主要借鉴金融工程的理论和方法。

连锁零售企业供应链是从供应商的供应商到客户的客户，由众多首尾相连、错综复杂的供需长链组成，它的这种多参与主体、多环节、多目标的特征组成的系统非常复杂。由于供应链风险处于这种复杂的系统中，因此需要考虑的因素很多，这些因素可能分属不同的级别。在对这样复杂系统的风险进行综合评判时，为了便于区分各因素在总的评价中的地位和作用，全面地吸收所有因素所提供的信息，需要考虑从各个层次对供应链整体风险的影响，如供应链各个节点企业、各个运作环节的风险对供应链整体风险的影响。而在实际运作中，也需要从不同的层次对供应链风险进行管理，所以这里对供应链风险评价体系建立了基于多个级别的新构架。

由于不同供应链其节点企业的种类和数目不同，且影响供应链和每个节点企业风险的类别和数量也有所区别。

模糊综合评价结果向量是通过构造等级模糊子集把反映被评价事物的模糊指标进行量化（即确定隶属度），然后用模糊变换对各指标综合，一般需要以下步骤进行：

（1）确定评价对象的因素论域：P个评价指标，u={u₁，u₂，…，u_p}。

（2）确定评语等级论域：v={v₁，v₂，…，v_p}，即等级集合。每一个等级可对应一个模糊子集。一般情况下，评语等级n取3～7中的整数，评价集合可选取{强、中、弱}、{好、较好、一般、较差、差}等表示。

（3）建立模糊关系矩阵R：在构造了等级模糊子集后，要逐个对被评事物从每个因素u_i（i=1，2，…，p）上进行量化，即确定从m个单因素来看被评事物对等级模糊子集的隶属度（R|u_i），进而得到模糊关系矩阵：

从评判矩阵R中第i行第j列元素r_ij可以看出，表示某个被评/决策事物从因素u_i来看对v_j等级模糊子集的隶属度。一个被评事物在某个因素u_i方面的表现，是通过模糊向量（R|u_i）=（r_i1，r_i2，…，r_im）来刻画的，而在其他评价方法中多是由一个指标实际值来刻画的，因此从这个角度讲模糊综合评价要求更多的信息。

（4）确定评价因素的模糊权向量：W=（w₁，w₂，…，w_p）在模糊综合评价中，权向量W中的元素w_i本质上是因素u_i对模糊子集{被评价事物重要的因素}的隶属度，因而用一般模糊方法来确定，并且在合成之前要归一化。其步骤一般如下：

1）利用合适的合成算子将W与被评事物的R合成得到各被评事物的模糊综合评价结果向量X。

2）用模糊权向量W将不同的行进行综合就可以得到被评事物从总体上来看对各等级模糊子集的隶属程度。模糊综合评价的初始模型可表示为如下的模糊变换关系：

X=W⋅R

式中，权重集W可看作为一行p列的模糊矩阵。上式按模糊矩阵乘法进行运算，就可以获得模糊综合评价结果向量。

3）对模糊综合评价结果向量进行分析：实际中最常用的方法是最大隶属度原则，但在某些情况下使用会有些很勉强，损失信息很多，甚至得出不合理的评价结果。目前，一些学者提出使用加权平均求隶属等级的方法，对于多个被评事物并可以依据其等级位置进行排序，在有些情况下评价结果更有效。(www.daowen.com)

可见，模糊综合评判就是应用模糊变换原理和最大隶属度原则，考虑与被评价事物相关的各个因素，对其所做的综合评价。这里评价的着眼点是各个相关因素。

近年来由于社会与科技的发展，评价对象的系统复杂性与层次性不断增加。就目前利用模糊综合评判方法来研究连锁零售企业供应链风险评价的应用深度来讲，一方面在进行评判时对于评判因子一般采用的是一级评判，针对连锁零售企业供应链这种复杂系统，由于其成灾因素很多，且各因素之间往往还有层次之分，如果采用一级评判，就难以比较系统中事物之间的优劣次序，得不出有意义的评判结果。另一方面，在评判时对于隶属函数的构造虽有很多方法，但对于评判因子与风险度之间关系的描述，目前还没有一个很好的方法和函数能够准确刻画，原因在于影响连锁零售企业供应链风险产生的因素具有复杂的非线性关系，一般的线性解法很难建立一个实用的模型。

此外，在选取评判因子时，由于没能很好地结合具体研究的连锁零售企业供应链的风险特点来选取合适的评判因子，或是遗漏了关键的评判因子，或是增加了一些与风险危害度关系甚微的因子等，都有可能导致评判效果欠佳。

多级模糊综合评价是利用模糊数学方法对某一系统的各个指标进行综合评价的新体系，它可以正确反映系统内部综合因素相互作用的过程，有利于对各个复杂系统进行合理的评价。基于此，近年来为了克服不断庞大、复杂的供应链风险评价需求，多级模糊评判以及非线性的隶属函数，在供应链风险评价与考量中应用的越来越广泛。

多级模糊综合评价模型的基本概念如下：

定义2.23 多级模糊综合评价模型是一个七元组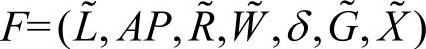其中，

1）指标体系之集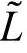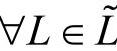，，L={l₁，l₂，…，l_m}记录某一级评价指标；

2）评价等级之集AP，AP={a₁，a₂，…，a_n}表示评价等级；

3）评价矩阵之集，，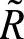

R记录存储某一级的隶属函数矩阵即评价矩阵，R中的元素r_ij表示本级评价第i个指标在第j等级上的隶属度，且r_ij∈[0，1]；

4）模糊权重之集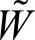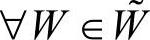，，W=(w₁,w₂，…，w_m)，W的元素计算存储某一级各评价指标的权重，W中的元素w_i表示本级评价第i个指标在评价时的权重，r_ij∈[0，1]，且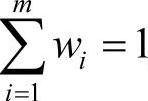，否则要进行归一化处理；

5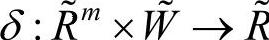）为评价函数，，δ（R₁，…，R_m，W）=R′表示低一级评价矩阵R₁，…，R_m向高一级评价矩阵R′的模糊合成过程；

6）赋值矩阵之集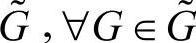，G=[g₁，g₂，…，g_n]^T计算存储某一级评价指标的得分；

7）得分之集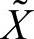，，记录某一级评价得分，多级综合评价一般只需对最高级评价结果进行评价、打分。