属性约简又称维规约或特征选择，属性约简主要是为了解决高维数据计算的复杂性和准确性问题。目标是消除冗余和不相关属性对计算过程和最终结果造成的影响。

对数据进行属性约简的意义，主要从以下几个方面考虑：

1）从机器学习的角度来看，通过属性约简去除噪声属性是非常有意义的；

2）对一些学习算法来说，训练或分类时间随着数据维数的增加而增加；

3）经过属性约简可以降低计算复杂度，减少计算时间；

4）假如不进行属性约简，噪声或不相关属性和期望属性对分类的作用一样，就会对最终结果产生负面影响。

当用较多的特征来描述数据时，数据均值表现得更加相似，难以区分。由2.3.3节论述可知，连锁零售企业供应链风险指标层次繁杂、因素众多，通过属性约简，达到简化原有风险评价与预警研究的目的。

属性约简是粗糙集理论（Rough Set）的核心内容之一，它刻画了决策知识表中的本质部分。通过冗余属性的约简与除去，减少资源的浪费（仅需要较小的存储空间）；另一方面，有利于去除干扰，便于人们做出正确而简洁的评价与决策。

粗糙集理论是由波兰Pawlak教授于20世纪80年代提出的一种研究不完整、不确定知识和数据的表达、学习、归纳的理论方法，近些年在理论模型、算法研究、工程应用上得到了广泛的应用并取得了好的成果。下面对粗糙集的概念进行简单的介绍。

粗糙集理论的主要思想是利用已知的知识库，将不精确或不确定的知识用已知的知识库中的知识来刻画。知识直接与真实或抽象世界的不同分类模式联系在一起，任何客观事物，都可用一些知识来描述，知识可以被理解为对事物的分类能力，知识分类能力也可用知识系统的集合表示形式来描述。

定义2.1 一个知识库可以表达为

K=（U，R）

式中，U为对象的有限集合，即论域；R为U上的等价关系。

上近似集与下近似集定义2.2给定知识库K=（U，R），X⊆U，等价关系r⊆R，则X关于等价关系r的上、下近似集分别定义如下：

bn_r（X）=r^-（X）-r_-（X），定义为X中不能被U/r精确表示的元素集合，称X的r边界域。这里，r_-（X）也称为X的r正域，表示完全能被U在r下的等价类精确描述的X的子集，U-r_-（X）称为X的r负域，表示论域U中肯定不属于X且能够被U/r精确描述的部分。

信息系统与决策表中信息系统（即知识表达系统），通常采用二维表来表示，因此可称为信息表。信息系统的表达法是一种形式语言，列由属性的取值构成，由对象构成。知识库与信息系统存在一一对应关系，知识库中任何一个等价关系的等价类都可以用属性和该属性下的属性值表示。

定义2.2 一个信息系统表达为

S=（U，A，V，f），简记为S=（U，A）.

式中，U为对象的集合U={x₁，x₂，…，x_n}，也称为论域；A为非空有限属性集合；V为属性值的集合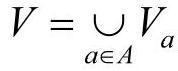，，V_a表示属性a的取值范围，即属性a的值域；f：U×A→V是一个信息函数映射，它为论域U中每个对象的属性指定唯一值。

定义2.3 决策表是一种特殊的信息表，可以用T=（U，A=C∪D，V，f）表示，其中C表示条件属性集合；D表示决策属性集合，且D≠Φ。通常，为了讨论方便，也可以记为T=（U，A，C，D），称为CD决策表。

知识与信息熵是近代不确定性理论的研究基础，Pawlak提出的粗糙集理论是基于代数观点进行描述的。近几年来，一些学者从信息论、概率论的角度对粗糙集理论重新进行了研究和扩展，将对粗糙集理论中的知识做了新的理解，建立知识与信息熵之间的关系。

给定信息系统S=（U，A，V，f），其中U为论域，A为非空属性集合（即等价关系族或知识）。

定义2.4 设P和Q为论域上U上的等价关系族（即知识），U/ind（P）={X₁，X₂，…，X_n}，U/ind（Q）={Y₁，Y₂，…，Y_n}，则P、Q在U上的子集的概率分布分别为

其中，；。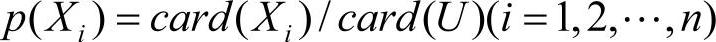

有了知识的概率分布定义后，就可以根据信息论来定义知识的自信息熵、联合熵、条件熵、互信息等概念。

定义2.5 知识（属性集合）C的自信息熵定义为

定义2.6 知识（属性集合）D相对于知识（属性集合）C条件熵定义为

其中，。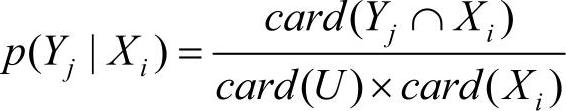

粗糙集中离散化的基本理论在利用计算机进行分析、评价的研究中应用广泛，由于RoughSet理论产生于集合论，集合论元素又是以独立个体形式存在的，因而在运用粗糙集理论进行决策表的属性约简前，都必须先将具有连续变化的实数属性值做离散化处理，选取适当的断点区间来对条件属性构成的空间进行划分，把这（为条件属性个数）维空间划分为有限的区域，使得每个区域内对象的决策值相同。离散化后的决策表减少解决问题时的复杂度，可以很好地提高适应性。

决策表S=（U，Q，V，f），设其决策属性个数为r（d），c为实数集。属性a的值域V_a上的一个断点可以记为（a，c），其中a∈Q。在值域V_a={l_a，r_a}上任意一个断点集合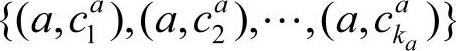定义了V_a上的一个分类P_a：

因此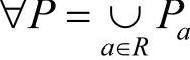，定义一个新的决策表S^P=（U，Q，V^P，f^P），f^P（x_a）=i⇔f（x_a）∈[c^a_i，c^a_i+1]，对于x∈U，i∈{0，1，…，k_a}，经过离散化处理之后，一个新的信息系统决策表取代了原来的信息系统决策表。

RoughSet理论的优势在于它不需要额外的参数和先验知识，直接根据数据库或信息本身就可以进行离散化。离散化算法有等距划分算法、等频划分算法、NaïveScaler算法、SemiNaïveScaler算法、布尔逻辑和Rough集理论相结合的离散化算法、基于断点重要性的离散化算法及基于属性重要度的离散化算法等。

粗糙集属性约简是Rough集理论研究中的一个关键性问题，也是粗糙集理论中—个重要的研究课题。属性约简就是从原始属性集中去除不相关的、冗余的、具有干扰性的非重要属性，找出具有重要意义的属性子集的过程。通过属性约简建立一个更简洁、更精确的学习模型，可极大地减少规则抽取算法的计算时间，提高导出模型的准确性。

定义2.7 给定一个信息系统S=（U，A），对于每个属性子集B⊆A，可构造对应的二元等价关系：

称ind（B）为由B构造的不可分辨等价关系。

定义2.8 给定一个信息系统S=（U，A），令P、Q为U中的等价关系，则Q的P正域可定义为

对于U/P的分类，U/Q的正域是论域U中所有通过分类U/P表达的知识一定能够划入U/Q类的对象的集合。若P、Q为U中的等价关系族，由它们构造的不可分辨关系分别为ind（P）、ind（Q），则Q的P正域可表示为

定义2.9 给定一个信息系统S=（U，A），对于属性集合P、Q、R，称R为P的Q约简，当且仅当同时满足以下两个条件：

1）POS_ind（R）（ind（Q））=POS_ind（P）（ind（Q））；

2）不存在属性a∈R，使得POS_{ins（R-{r}）}（ind（Q））=POS_ind（P）（ind（Q））成立。将所有P的Q约简用RED_Q（P）来表示。

定义2.10 P的相对于Q的核CORE_Q（P）定义为

CORE_Q（P）=∩RED_Q（P）(www.daowen.com)

也就是说P的Q核CORE_Q（P）是所有P的Q约简的交集。

定义2.11 给定一个决策系统T=（U，C∪D，V，f），对于条件属性子集R⊆C，若满足：

1）POS_ind（R）（ind（D））=POS_ind（C）（ind（D））；

2）不存在属性a∈R，使得POS_{ins（R-{r}）}（ind（D））=POS_ind（P）（ind（D））成立。则称R为条件属性集C相对于决策属性集D的相对约简，所有C的D约简可记为RED_D（C），很显然有R=RED_D（C）。

连锁零售企业供应链风险预测与预警研究由于机理复杂，目前主要是依靠数据进行分析和挖掘。在利用粗糙集理论处理决策表时，要求决策表中各值用离散值表达，因此一些连续值的离散化方法有研究的必要。

通常，决策信息表建立后，实际的风险指标约简问题转换为应用粗糙集理论处理决策信息表的数学问题了。对条件属性进行属性约简，首先需要对决策表进行离散化处理。本节介绍使用Semi Naive Scaler算法对决策表进行离散化处理，该算法方便、快捷且可行性较高。

Semi-NaiveScaler算法是NaiveScaler算法的改进算法。由于NaiveScaler算法在离散化处理过程中考虑的因素不全面且选取的断点太多，因此可以通过优化断点集来减少断点的数目，由此形成了Semi-NaiveScaler算法。

该算法按照属性值的大小，对决策表中的数据从大到小排序：

X^a_i={x∈U|a（x）=v^a_i} （2-8）

其中，。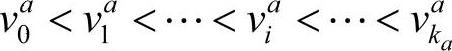

然后处理断点通过以下公式：

式中，v^a_i为条件属性的值；v_i为决策属性的值；C^a为属性断点集合；集合D^a_i为X^a_i中主要的决策属性值，即等价类X^a_i中出现频率最高的决策属性值。

Semi-NaiveScaler算法的基本步骤如下：

1）依照式（2-7）和式（2-8）计算X^a_i和D^a_i的值；

2）如果D^a_i∉D^a_i+1，且D^a_i+1∉D^a_i，则根据式（2-9）得到相应的断点值；若不满足条件，则不选取此断点。

Semi-NaiveScaler算法求出的断点数目要小于NaiveScaler算法所求得的断点数目，去掉了NaiveScaler算法中的一些不必要的断点。实际上它所求得的断点是NaiveScaler算法断点的一个子集。

知识约简是粗糙集理论研究中的重要内容之一，它具有属性约简和属性值约简两种形式，其基本思想是在保持信息系统分类或决策能力不变的基础上，删除不相关或不重要的冗余属性或冗余属性值，获得信息系统的分类或决策规则。伴随数据库系统中数据的不断扩大，属性约简变得更加具有实际价值，它简化了数据库结构的复杂度，提高人们对隐含在庞大数据量下的各种信息的认识程度。因此，属性约简成了目前粗糙集理论研究的热点之一。目前人们针对属性约简做了很多的研究，提出了许多相关约简算法。

1.辨识矩阵法

辨识矩阵是由数学家A.skowron提出来的，在粗糙集约简过程中，通过辨识矩阵表达出复杂信息系统中存在的全部不可区分关系。通过构造区分矩阵得出相关的区分函数，然后应用吸收律化简区分函数，使之成为析取范式，则每个值蕴含式均为约简。这种算法简单直观、易于理解，很容易得到信息系统中属性核与所有约简。但同时该算法的缺点也十分明显：当属性的规模较大时，差别矩阵占有大量的存储空间O（n²），不具备可操作性，其时间复杂度随条件属性呈指数增长，无法处理大规模数据集。

2.启发式约简算法

目前各种启发式算法很多，根据对属性重要度的定义不同可分为基于属性重要度的启发式算法、基于条件信息熵的约简算法、基于属性频率的启发式算法等。这些算法都以信息系统或决策表的核为起点，依次选择属性重要度最大的属性加入核中，直到满足终止条件，最后得到的属性集合就是信息系统或决策表的最优约简。由于信息系统中各个属性不是孤立存在的，且相互之间存在着联系和影响，所以采用属性重要度的启发式约简算法有时不能找到信息系统的最优解。目前，国内外学者已经提出了几种经典的属性约简算法，主要可分为两类：

1）基于属性重要性程度逐步扩展的算法，该算法是从空集开始搜索，缺点是计算量较大。

2）基于属性重要性的启发式算法，该算法首先计算求出决策系统的相对核，然后逐步扩展求出一个较优的相对属性约简。这种启发式的属性约简算法，主要包括基于分类质量的约简算法、基于依赖度的约简算法、基于差别矩阵的约简算法和基于信息论的约简算法等。其中基于分类质量的算法、基于依赖度的算法分别利用了粗糙集理论中的分类质量和依赖度的概念；基于差别矩阵的算法通过生成差别矩阵，然后根据差别矩阵中属性出现的频率来定义属性的重要性，该方法比较直观，但其确定需要生成差别矩阵，需要较大的时间复杂度和空间复杂度；基于信息论的算法则是将信息论、概率论引入到属性约简中，通过决策属性与条件属性之间的互信息、条件熵或其组合的方式来度量条件属性的重要性。

a）基于分类质量的启发式算法：

定义2.12 设T=（U，A，V，f）为一个决策表信息系统，其中U表示论域；A=C∪D是属性的非空有限集合，属性子集C和D分别为该决策表信息系统的条件属性集和决策属性集，且有条件属性子集R⊆C，则分类质量定义为

r_R=card（POS_ind（R）（D））/card（U）

则用属性a∈C−R添加到条件属性子集R时分类质量r_R的增量来表示属性a的重要性，即

SGF（a，R，D）=r_R∪{a}-r_R

根据上述以分类质量增量作为属性重要性的定义，提出了基于分类质量的启发式算法。

b）基于依赖度的启发式算法

定义2.13 设T=（U，A，V，f）为一个决策表信息系统，其中U表示论域；A=C∪D是属性的非空有限集合，属性子集C和D分别为该决策表信息系统的条件属性集和决策属性集，且有条件属性子集R⊆C，Hu等定义条件属性子集R与决策属性集合D之间的依赖度为

k（R，D）=card（POS_ind（R）（ind（D）））/card（POS_ind（C）（ind（D））

很显然0≤k（R，D）≤1，值k（R，D）描述了决策属性D和条件属性子集R关联性，如果R是C的相对于D的约简，则有k（R，D）=l；如果为空集（即R=Φ），则有k（R，D）=0。Hu等用属性a∈C−R添加到属性子集R时依赖度k（R，D）的增量来表示属性a的重要性，即

SGF（a，R，D）=k（R∪{a}，D）−k（R，D）

式中，SGF（a，R，D）为当前选择的条件属性子集为R时，属性a的重要性（其中属性a∈C−R），它反映了将属性a添加到R中依赖度的增量，依据上述以依赖度增量作为属性重要性的定义，提出了基于依赖度的启发式算法。

c）基于差别矩阵的启发式算法：

定义2.14 设T={U，A，V，f）为一个决策表信息系统，其中U表示论域；A=C∪D是属性的非空有限集合，属性子集C和D分别为该决策表信息系统的条件属性集和决策属性集，且有条件属性子集R⊆C，将属性a∈C−R的重要性定义为差别矩阵中属性出现的频率，即

SGF（a，R，D）=p（a）

式中，p（a）为差别矩阵中删掉与属性子集中属性有交的属性组合的剩余部分所出现的频率，提出了基于差别矩阵的启发式算法。

d）基于信息论的启发式算法：

信息论是美国数学家香农为解决通信过程中遇到的一些问题而建立的一系列理论。一个传递信息的通信系统由信源、信宿以及连接两者的信道组成。信息是确定性的增加，用来消除不确定性的；信息量的大小由所消除的不确定性来度量。从信息论观点研究粗糙集理论的属性约简算法，大多数都采用条件熵、互信息以及两者之间的组合方式来定义属性的重要性，然后得到相应的启发式算法。