可以用利率期间结构模型对未来利率进行预测。

每一种不同期限的债券都有一个价格，以及一个与之相对应的利率，叫做到期收益，或者简单地叫做收益。观察任何一天的不同期限债券的收益，可以画出收益和期限之间关系的轨迹，这个关系就叫做收益曲线 （yield curve），或者利率的期限结构 （term structure of interest rate）。图10-5显示了1993年1月1日和1998年7月22日美国政府债券的期限结构。1993年1月的收益曲线非常陡峭，3个月期的国库券利率只有3%，但30年期的利率是7.34%；而1998年7月的收益曲线非常平坦，3个月期利率比1993年1月高2%，30年期利率却低1.5%，从而使得3个月期和30年期利率之间的差异小得多。一条陡峭的收益曲线能告诉我们关于金融市场预期的什么信息？

图10-5美国的收益曲线：1993年1月和1998年7月

1.债券价格的决定

不同期限的债券价格之间具有什么关系？

对于1年期债券，令当前的1年期利率为i_1t ，面值为100元人民币的1年期债券价格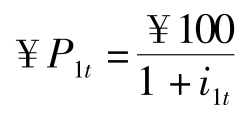：，1年期债券的价格与当前的1年期名义利率反向变化。实际上，由债券市场决定的其实是1年期债券的价格，然后由价格推知1年期利率：（¥ 100-¥ P_1t/¥ P_1t ）。

对于2年期债券，面值100元的2年期债券价格

其中，i_1t是今年的1年期利率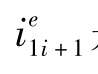，是金融市场预期的明年的1年期利率。

同样的方法，可以写出n年期债券的价格。

套利和债券价格

设想可以在持有1年期债券和2年期债券中进行选择，1年后两种债券的回报：

对于1年期债券，投入1元，第2年会得到1＋i_1t元。对于2年期债券，可以在当前买入1/＄P_2t份债券，到了第2年，债券距到期日仅有1年，因此成为一种1年期债券，第2年预期的出售价格是¥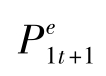，因此，对2年期债券每投入1元，第2年预期会得到¥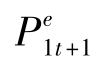/¥ P_2t 元，见图10-6。

图10-6 持有1年期债券和2年期债券1年的收益(www.daowen.com)

在这个假定下，如果经济中1年期债券和2年期债券的量都是正的，就可以认为两种债券必须提供同样的预期1年期收益率：

左边表示持有1年期债券1年1元可以获得的收益，右边表示持有2年期债券1年1元可以获得的预期收益。两种选择的预期收益必须等价的关系叫做套利关系。改写上式：

套利意味着今天2年期债券的价格是明年债券的预期价格的现值，那么，1年期债券明年的预期价格¥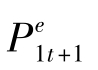怎样决定呢？这个问题并不难，因为1年期债券今年的价格依赖于今年的1年期利率，所以1年期债券明年的价格依赖于明年的1年期利率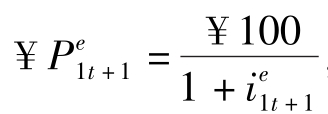，，明年的债券预期价格等于最后一次支付额100元，用明年的1年期预期利率贴现。以上两式综合：

套利和现值之间的关系：不同期限债券之间的套利意味着债券价格等于这些债券的预期收益的现值。

2.债券收益的决定

不同期限的债券收益之间的关系

一个n年期债券的到期收益 （yield to maturity），或者等价地，n年期债券的利率，其定义为一个不变的年利率，它使得债券当前的价格等于其未来收益的现值。以2年期债券为例，将其收益记为i_2t ，则¥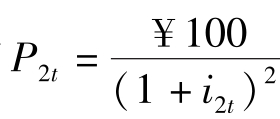^，将这个收益定义为一个不变的年利率，它使得2年后的100元的现值等于债券当前的价格。

假定债券现在的售价为90元，那么2年期利率i_2t通过下面的等式求得：

2年期利率和当前1年期利率以及预期1年期利率的关系：

上式很直观，也很重要，它说明了2年期利率近似等于当前1年期利率以及明年的预期1年期利率的平均值，这个关系可以推广到更长期限的债券利率上。n年期利率近似等于当前以及未来n-1年的预期1年期利率的平均值：

这个关系式指出了我们解释收益曲线的关键。一条向上的收益曲线说明金融市场预期的短期利率在将来是上升的，一条向下倾斜的收益曲线告诉我们金融市场预期的短期利率在将来是下降的。回到图10-5的1993年的收益曲线，可以推断出金融市场对1年后 （1994年1月） 1年期利率的预期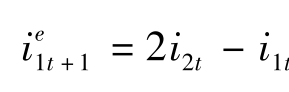：_t ，在1993年1月，i_1t是3.5%，2年期利率是4.4%，因此，1994年预期1年期利率等于 （2×4.4%）-3.5%=5.3%，比1993年1月的1年期利率高1.8%。收益曲线的斜率揭示了金融市场对未来短期利率的预期。