为求解一个参数化的RBC模型，设置以下参数值：

（β=0.99，α=0.36，δ=0.025，A=3）。这意味着稳定状态值是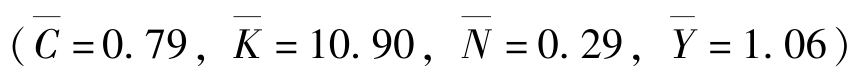：。这些值意味着代表性家庭将30%的时间用在工作上，资本产出比率接近10 （产出是季度数据）。剩下的参数值决定了技术冲击的行为。依据索罗残差定义Z_t =ln Y_t -αln K_t -（1-α） ln N_t。Z_t序列可以按照一个线性趋势来进行回归 （这与固定技术进步的假设相一致）。残差即技术冲击Z_t。麦可格兰坦 （1996）^[7]对美国1960.1-1994.4期间的季度数据进行拟合，得到Z_t的序列相关系数一个估计 （参数ρ） 大小为0.95，技术冲击的方差估计为0.007。技术冲击的方差是与求解模型的线性解不相关的，但是，当模型的解被用来在模拟经济中产生人工的时间序列时，必须约定这一参数的值。

这些值生成了下面的A、B矩阵：

上式左乘A^-1，得到：

接下来，将A^-1B分解为QΛQ^-1，并左乘Q^-1，得到：

矩阵Λ中的项 （即A^-1B的特征值） 决定了解的大小。第二个对角项是ρ^-1。

Λ矩阵的第四行是与期内有效条件相联系的。这些值等比例于矩阵A中的一行给定的值；将所有的项除以 （-2.62） 得到了原来的期内有效条件。矩阵Λ中剩下的两项是与稳定状态解的鞍点路径性质相关的。

因为稳定理性预期解是与小于1 的特征值相联系的，因此Q^-1矩阵的第三行提供了我们寻找的线性约束。即，理性预期解是：

资本运动法则 （矩阵A的第三行决定了其参数值） 以及期内有效条件提供了额外两个均衡条件：

接下来可以用随机数值产生一系列技术冲击，上面的方程就可以用来模拟生成资本、消费、劳动力和产出的时间序列。(www.daowen.com)

方程 （6-16） 至 （6-18） 刻画了模型的解，给定初始的资本水平，并产生一条外生技术冲击路径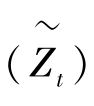，这些方程将生成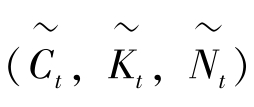的时间序列。另外两个宏观经济学感兴趣的序列，即产出和投资序列，可以通过线性化生产函数和资源约束得到。

具体地，对产出来说，线性化假设的柯布-道格拉斯生产函数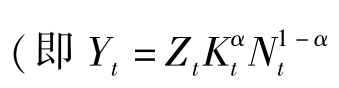并使用测定值α=0.36） 得到下面的方程：

最后，均衡时的条件产出等于消费和投资之和，对其做线性逼近，可以表达为下面的离差形式：

使用数值解中的稳定状态值，投资方程成为：

因此，这一经济的均衡由下列方程刻画：

为了得到模型下的各时间序列，先要产生技术冲击扰动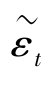的一个序列，假设其均值为零，方差与实际观察到的一致，即如前所述，方差为0.007。接下来，初始化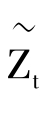=0并使用一个随机数生成器来生成扰动，从而产生技术冲击。然后，假设所有剩下的值最开始处于稳定状态 （意味着所有的初始值设为零），可以解上面的方程组，并得到内生变量的时间路径。接下来可以把人工产生的各种变量的时间路径画出来，与实际变量路径进行比较。从中可以发现RBC产生的路径与实际路径的拟合度、相似度等。

实际经济周期研究方法现在有广泛的应用，它被使用在货币经济学、国际经济学、公共财政、劳动力经济学、资产定价等各个领域。在早期真实经济周期理论中，“技术冲击”是一个重要的假定，不过，进入20世纪90年代，实际经济周期理论逐渐突破 “技术冲击” 的限制，拓宽到供给冲击的各个方面，详见金姆和洛嘉尼 （1992）^[8]；诺特博格和伍德福德 （1996）^[9]；奥海宁 （1997）^[10]；雷拜罗 （2005）^[11]；夏默 （2009）^[12]等。

实际经济周期模型的理论意义：首先，其方法论上的特点就是把经济增长和经济波动的研究方法结合在一起。因此，RBC模型被大多宏观经济学家视为当今最好的经济周期模型。其次，BRC模型从微观经济主体的最优化行为出发建立模型，使实际商业周期建立在坚实的微观经济基础之上。这一方法，已经成为现代宏观经济分析的主要分析方法。当然，实际商业周期理论模型也存在缺陷，主要表现在模型构造上既没有考虑政府的作用，也完全忽略了货币对经济的影响，由于这两点都脱离了实际情形，使其对经济周期的解释能力大打折扣。

随着时代的发展，RBC 模型在很多方面都获得了很大的改进，但它还是以瓦尔拉斯的完全竞争一般均衡理论作为其核心框架。这使得其忽略了现实中普遍存在的市场非完全竞争性以及由此导致的价格不完全灵活调整，即存在价格 （一般商品价格、工资等） 粘性。与此同时，RBC 模型中宏观经济政策 （财政政策和货币政策） 的作用微乎其微，这与大量货币政策有效性实证研究相悖。这些直接促使了 20世纪90年代出现的将RBC 理论和新凯恩斯主义假设 （价格粘性和垄断竞争） 进行融合的动态随机一般均衡 （DSGE） 模型的发展。