第一步，推导均衡条件。每一时期，代表性家庭都要进行决策：给定了初始时期的资本存量和当前的技术冲击，选择消费、劳动力和投资。假设效用函数具有时间可分性，也就是说时间t的消费和劳动力选择不会影响其他时间消费和休闲的边际效用。把最大化问题转化为下面的动态规划问题：

t时期的状态变量：（K_t ，Z_t ）

t时期的控制变量：（C_t ，N_t ，K_t＋1 ）

要得到上述问题的一个解必须满足下面的必要条件和资源约束：

(S1) U_2,t =U_1,tZ_t F_2,t

(S2) U_1,t =βE_t{U_1,t＋1［Z_t＋1 F_1,t＋1 ＋(1-δ)］}

(RC) K_t＋1 =Z_t F(K_t,N_t) ＋K_t(1-δ)-C_t

S1表示期内有效条件 （劳动-休闲权衡），它暗示了劳动与消费之间的边际替代率一定等于劳动的边际产量。其中 U_i，t （i=1，2） 表示效用对第i项的导数在 （C_t，1-N_t） 的取值；F_i，t （i=1，2） 含义解释与前者类似。S2代表了跨期有效条件，左边是用效用表示的投资在更多资本上的成本，右边则代表预期边际效用回报。在最优解时，这些成本和回报必须相等。RC为资源约束等式。

为简化分析起见，假设效用函数具有下面的形式：

这是经济社会中的一个稳定均衡，其假设技术冲击是固定的，因此不存在不确定性，即Z_t =1对所有的t成立：并且资本、劳动和消费的值都是固定的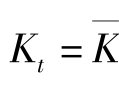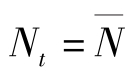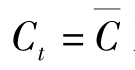，，，对所有的t成立。将这些稳定状态条件代入 （6-3），通过求解可以得到稳态值：

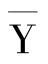表示稳定状态的产出水平。

给模型选择参数集合 （δ，β，A，α） 的值，使模型稳定状态解的行为符合数据的长期特征 （这一过程叫做校准，Callbar-tion）。依据数据的长期特征 （即没有周期性） 有：

（1） （1-α）=劳动产出占总产出的平均比率；

（2） β^-1 -1=平均无风险实际利率；

（3） 给定 （α，β），用 （SS2） 选择δ使得产出与资本比率与观察结果一致；

（4） 参数A决定了花在工作上的时间。这个结论可以从下面的推导得到：将 （SS1） 两边同时乘以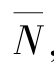，将表达式变形得到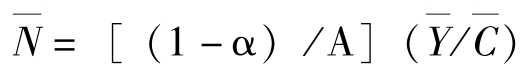，从稳定状态的资源约束条件 （SS3）可以推出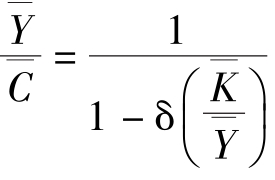，因此，通过前三步选择参数的过程可以得到产出和消费的比率，因此，A 的选择决定了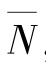，即劳动时间。

汉森和莱特 （1992）^[5]选择美国二战后数据进行参数测定，得出的典型参数值是：劳动力产出比率是64%，因此α=0.36；年无风险利率是0.04%，因此β=0.99；资本产出比率 （产出是基于季度数据衡量的） 为10，因此δ=0.025；30%的时间用来工作，因此A=3。

第二步，线性化。普雷斯科特 （1986）^[6]证明代表性家庭决策问题的解是存在且唯一的。但是不存在解析解，解由一系列资本、消费、劳动的策略函数组成。为使模型能够运行，要找到一个近似的数值解。最简单的方法之一是对这三个均衡条件以及技术冲击的运动方程在状态值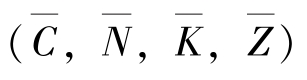附近做线性逼近 （如取一阶泰勒展开式）。(www.daowen.com)

对于期内有效条件Sl：

注意在最后一个表达式里，所有变量均被表示为稳定状态离差百分比的形式 （头两项调整了各自的倒数，而最后一项则利用了稳定状态时的事实）。因为稳定状态条件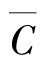=［（1-α）/A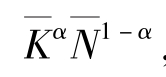］，上式两边均除以这一条件，就可以得到消费关于稳定状态的离差百分比形式。用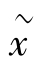表示变量与稳定状态的离差百分比，方程 （6-4） 可以写作：

对于跨期有效条件S2：

同样地，在稳定值进行线性展开，并用稳定状态离差变量表示，得到：

对于资源约束条件，同前面的步骤一样，在稳定状态附近线性化资源约束得到：

对于技术冲击过程，按照方程 （6-1） 所描述的自回归过程进行线性化得到：

对两边取期望，得

第三步，求解

方程 （6-5）、（6-6）、（6-7）、（6-9） 刻画了一个理性预期均衡，可以写成一个向量期望差分方程。令u_t =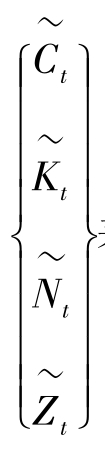表示一个向量，则方程的线性系统可以写作：

矩阵A和B分别是：

方程 （6-10） 两边同乘以A^-1 ，得到：

矩阵A^-1B可被分解为：

其中Q是一个矩阵，它的向量是A^-1B的特征向量，Λ是一个对角矩阵，它的对角元素是A^-1B的特征值。利用这一分解并用Q^-1左乘方程 （6-11） 的两边，得到：

注：定义的 （4×1） 向量d_t的元素是 （4×4） 矩阵Q^-1行向量各元素与 （4×1） 向量u，各元素的线性组合。由于Λ是一个对角矩阵，方程 （6-13） 暗示四个独立的方程：

由于方程 （6-14） 必须每一期都成立，通过不断迭代直到T期得到：

λ是与四个均衡条件 ［方程 （6-5） 至 （6-8）］ 相联系的四个不同的特征值。由于条件之一是与外生技术冲击方程 ［方程（6-8）］，其中一个特征值是ρ^-1。同样，矩阵A和B的第一行是由期内有效条件决定的；由于这不是一个动态关系，其中一个特征值为零。剩下的两个特征值必包括单位值l，因为由随机增长框架推出的鞍点路径均衡必定包括这一结果。由方程 （6-15） 知，期望差分方程稳定的，理性预期解是与值小于1的特征值相联系的。即，如果λ_i ＞1，则不断迭代将导致d_i，t→∞，这就不是一个可行的均衡。此外，为了使方程 （6-15） 对所有的T 均成立（同样取右边的极限），在λ_i ＜1的稳定状态，一定有d_i，t =0；这一限制提供了合意的解。即，d_i，t规定了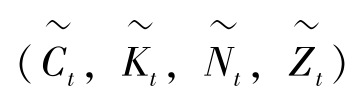与一个理性预期解一致的线性关系。［向量d_i的元素是 （4×4） 矩阵Q^-1行向量各元素与 （4×1） 向量u_t各元素的线性组合。］