考虑一个包含产出、通胀、利率三变量的递归系统模型：

上述模型具有惯性响应，利率对产出缺口的影响滞后一期；当期利率对通胀没有影响；货币当局利用利率规则对当期产出缺口和通胀做出响应。ε_1t为需求冲击，ε_2t为供给冲击，ε_3t为货币利率冲击。

拟合递归模型最简单的方法是先估计VAR之后利用乔分解（Cholesky decomposition），但下面的方法更常用。

一、 基本估计方法

EViews书写一个递归系统为：

这里lags是A₁ z_t-1 ＋……＋A_p z_t-p ，A可以被理解为建立结构方程中行为关系间的约束，B用于建立与脉冲响应联系的约束。因为EViews不允许约束A_j，j=1，2，……，p，只能指定A和B，先不考虑滞后项，重写式 （4） 为Ae_t =Bu_t，这里u_t =η_t是冲击，具有单位方差 （比较ε_t为非单位方差），这个表达式的逻辑来自单变量递归形式Az_t =A₁ z_t-1 ＋Bη_t ，代入VAR中的z_t =B₁ z_t-1 ＋e_t ，A （B₁ z_t-1 ＋e_t ）=A₁ z_t-1 ＋Bη_t整理得：Ae_t =（A₁ -AB₁ ） z_t-1 ＋Bη_t ，由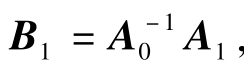，则 AB₁ =A₀ B₁ =A₁ ，Ae_t =Bη_t =Bu_t，相应地，应用EViews求解前要么设定初始矩阵A、B，要么设定等式Ae_t=Bu_t。

先估计VAR （2），然后选择 Proc→Estimate Structural Fac-torization，出现图1。

图1 给EViews填写Ae_t =Bu_t

选择text 或者 matrix，前者用于描述 A、B，而后者产生Ae_t =Bu_t。采用第一种方法的第一步是进行正交化，将式（1）-（3） 进行正交化，ε_jt =σ_jη_jt =σ_ju_jt ，A和B为：

因为要写出等式Ae_t =Bu_t ，然后让EViews执行最大似然估计求出 （A_j ，B） 中的未知参数，EViews中将约束性未知参数用C表示，设计如下：

以此填写图1。点击OK，EViews执行最大似然估计，结果见图2，给出估计系数C，对数似然值和估计的A、B矩阵：

图2 EViews 估计结构模型的A、B矩阵的最大似然估计结果

要获得脉冲响应，点击Impulse→ Impulse Definition→Struc-tural Factorization，得到乔分解同样的结果。

如果选择第二种方法Matrix，直接对EViews描述A、B。回到Eviews页面的顶部用 Object → New Object →Matrix-Vector Coef，产生一个空白矩阵，点击OK，设置行数和列数 （本例是3×3），点击OK，出现图3。

图3 一个矩阵对象的例子

用Edit＋/-键编辑这个列表，如图4。

图4 A矩阵的一个例子

这里 “NA” 意味着矩阵中需要估计的未知值，然后点击Name命名，称之为A。同样的步骤产生一个矩阵B。

冲击响应可用于观察在不同的预测范围对变量的冲击，执行冲击响应后，选择View → Variance Decomposition，用递归SVAR （2） 拟合，由需求冲击解释的通货膨胀的方差部分是15.92，供给/成本冲击解释的份额是75.85，而货币冲击是8.24，见图5。

图5 方差分解图示

估计递归模型的另一种方法是直接使用EViews中的System对象。在工作文件窗口，点击Object→New Object……，填写图6中的对话框，命名系统对象Macro-sys。

假设SVAR模型有两阶滞后，系统对象需要用EViews代码填充，见图7。

图6 产生一个System对象，命名为Chomor-sys

图7 在EViews系统对象中定义宏观经济模型

当期系数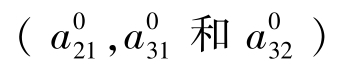的占位符是C （22），C （23）和C （24），点击Estimate，选择Full Information Maximum Likeli-hood，使用有约束的对角协方差矩阵，见图8。

图8 用完全信息最大似然进行系统估计

对应的SVAR模型中的A、B矩阵分别是

结果见图9。

图9 宏观经济模型完全信息最大似然估计的对角协方差矩阵

因为模型是完全识别的，意味着用一个用户设定的冲击矩阵A^-1 B进行累积的VAR能计算出冲击响应。见图10。

图10 计算冲击响应函数的EViews程序

冲击响应结果见图11。

在图11中对利率冲击的脉冲响应表明，在利率上升的情况下，通胀和产出对利率上升的反应是正的，而不是像理论预期的那样为负。这个例子说明递归模型的解可能产生一些反常现象，比如：

图11 宏观经济模型完全信息最大似然估计所得脉冲响应函数

价格反常——货币政策冲击对通胀有正作用；

汇率反常——提高利率的冲击使得货币贬值而不是升值。

要消除这些反常通常需要重新设定SVAR，当变量是稳定的时间序列时有四种方法可以尝试：

（1） 在系统中添加变量，即加入更多的冲击。本例中利率规则隐含的是货币供应方程，但系统模型中没有货币需求方程，因此，可以给系统增加一个货币变量，比如使用M1，M2，非借入外汇储备 （NBR），或者货币指数，这些都是在许多文献中用过的变量。西姆斯 （1980）^[9]为解决价格反常问题在模型中尝试加入石油价格或更一般的大宗商品价格等影响政策设定和通胀的因素，他的研究证实，给方程添加因子的确可以消除一些反常。

（2） 改变变量的形式。比如模型中是使用GDP，产出缺口，还是使用GDP增长率，或在结构方程中对对数GDP使用时间趋势，需要斟酌。西奥达尼 （2004）^[10]用美国国会预算办公室数据测度SVAR中美国的产出缺口，相比使用产出水平，大大减轻了价格反常问题。

（3） 改变模型设定。比如使用非递归系统或对冲击影响施加约束。克姆和鲁比尼 （2000）^[11]通过允许汇率对利率的当期影响来解决汇率反常问题，那样模型不再是递归的。

（4） 引入潜在变量，使现在的冲击多于可观察变量数。这样做的原因是，使用标准的SVAR意味着冲击数量等于可观察变量的数量，如果潜在的变量没有被放置在系统中，那么来自可观察的脉冲响应是更多的冲击次数的组合，这可能会导致冲击识别困难，引起价格反常。卡斯特洛诺沃和苏里科 （2010）^[12]的研究则认为系统的一些不确定性，即存在 “太阳黑子” 冲击是造成价格反常问题的根源。

二、 对冲击响应施加约束

对冲击响应施加一个零当期约束，即一个冲击对一个变量的当期影响是零，以一个三变量的VAR和SVAR冲击之间的关系为例：

这里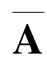就是B，具有元 {b_ij}，施加一个约束，b_ij =0意味着e_it不依赖于η_jt。

假设货币政策冲击η_3t对产出 （由e_1t表示） 和通胀 （由e_2t表示） 没有当期影响；需求冲击η_1t对通胀没有当期影响，这意味着：

这个冲击约束模型中有六个未知参数，因此是完全可识别的。它也与前面递归模型拟合有完全相同的似然函数 （在观测上是等价的）。因此，不可能在递归模型和基于数据匹配的冲击约束模型之间进行选择。需要其他标准来证明选择哪一个具有合理性。

施加零约束，依据EViews程序，式 （5）-式 （7） 意味着B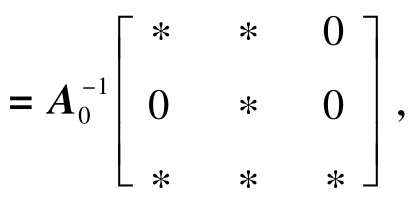在EViews中VAR页面，Proc→Estimate Structural Factorization→Text填写：

＠e1=c (1)∗＠u1＋c (2)∗＠u2

＠e2=c (3)∗＠u2(www.daowen.com)

＠e3=c (4)∗＠u1＋c (5)∗＠u2＋c (6)∗＠u3

用SVAR估计方法得到估计结果见图12。

图12 约束SVAR模型的输出

结果中的A₀矩阵为

注意本例中SVAR表达式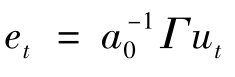，这里Γ是一个含有结构误差的标准离差的对角矩阵。EViews报告最终估计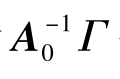作为 “估计的” B矩阵，A₀的估计需要推导。首先，将估计的B矩阵求逆，产生Γ^-1 A₀；其次，由于它的对角元不是1，需要每一行除对角元的值。图12估计的B矩阵求逆得：

图13给出在此约束下对利率冲击的脉冲响应，尽管加了约束，仍然存在价格和产出异常问题。

图13 假设货币和需求冲击为零效应的利率响应

现在考虑零脉冲响应对一个一般的 SVAR 的含义。由式（6） 知z_jt =e_jt ＋lags，z_2t =lags＋ε_2t ，ε_2t是结构等式z_2t的误差，所以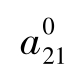，=0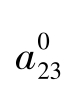，=0意味着这样一个结构系统：

这样，第1个和第3个等式需要工具变量，先从第3个等式开始，需要两个与ε_3t无关的工具。从 （5） 式知，很明显e_1t不依赖ε_3t （因为 ε_3t是 η_3t的倍数），由 （6） 式知，e_2t也不依赖ε_3t。所以，e_1t和e_2t能作为 （10） 式中z_1t和z_2t的工具。因为不知道e_1t和e_2t ，必须用VAR的残差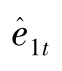和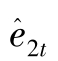作为工具。当然式 （8）可以用OLS估计，因为没有内生变量。

Quick→Estimate Equation，选择LS-Least Squares （NLS and ARMA）。在模型设定窗口填写：

gap gap(-1) gap(-2) infl(-1) infl(-2) ff(-1) ff(-2)

点击OK，给出参数估计。保存残差到工作文件中，点击Proc →Make Residual Series →OK，得到残差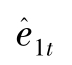，给残差命名“res1”；对通胀变量infl重复这一过程，给出残差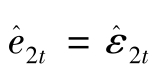（当方程没有内生变量时，VAR和结构误差是相同的），注意这些残差是自动保存到序列 “eps2”，图14显示程序。

图14 设置约束模型的工具变量并计算脉冲响应

对于第 （3） 式利率方程，用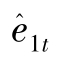和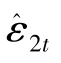作为z_1t和z_2t的工具变量。在屏幕呈现 OLS 估计结果后，点击 Estimate，在适当选择后，进行估计，然后填写模型设定：

ff gap infl gap(-1) gap(-2) infl(-1) infl(-2) ff(-1) ff(-2)

不选择 LS option，代之以选择 TSLS-Two-Stage Least Squares （TSNLS and ARMA），弹出Instrument List对话框，填入：

res1 eps2 gap(-1) gap(-2) infl(-1) infl(-1) ff(-1) ff(-1)

得到工具变量的估计结果后，用Proc→Make Residual Series用于产生含有方程残差的序列。称为 “eps3”，重复第1个等式的过程，模型定义为：

gap infl ff gap(-1) gap(-2) infl(-1) infl(-2) ff(-1) ff(-2)

所用的工具是：

eps2 eps3 gap(-1) gap(-2) infl(-1) infl(-2) ff(-1) ff(-2)

参数估计结果为：

B的对角元就是估计的方程误差的标准离差。工具变量法估计的参数与图12报告的用SVAR方法估计的结果是一致的。最后，不用下拉菜单的方法，用EViews的程序代码也可以做，见图14。

注意，如果第1个冲击对第k个变量的当期效应为零，意味着第 k个等式 VAR 残差能用作估计第 l个结构方程的工具（VAR工具原则）。

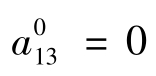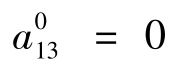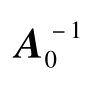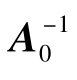工具变量方法的一个重要特征是它对结构VAR自动施加一个隐性约束，这一约束确保 e_1t （第1个等式的VAR残差） 不受η_3t的影响。通过设定，e_2t和e_3t （VAR残差） 正交于z_3t。加入滞后变量作为工具变量，z_3t被工具化，z_3t -lags=ε_3t ，由假设不影响 z_1t。另一种设定方法，是对=求逆，A0 内0元的位置具有与同样的结构，或将方程重新整理成递归结构，得到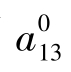=0。

通过再设定模型以便能将VAR残差与捆绑约束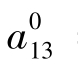=0结合起来，VAR工具原则也可以在System估计中使用。

图15给出EViews执行代码，C （22），C （23） 和C （24）对应于当期参数估计。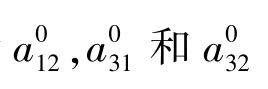

图15 对等式 （11）-（13） 进行EViews系统设定代码

用OLS估计系统对象产生输出，见图16，估计得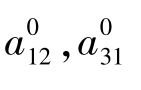和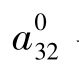与用工具变量法获得的相应值是匹配的。

最后，可以用完全信息最大似然FIML估计受约束系统和对角协方差矩阵选项，所需系统对象代码见图17，结果见图18，与工具变量法估计结果一致。

图16 等式 （11）-（13） 的非线性最小二乘估计

图17 等式 （8）-（10） 的EViews系统模型设定代码，假设a₁₃ =0

图18 等式 （8）-（10） 的FILM估计，假设a₁₃ =0

练习题

设计一个宏观经济模型并应用Eviews软件估计。

[1] R.E.Lucas,Econometric Policy Evaluation:A Critique,In The Phillips Curve and Labor Markets,K.Brunner and A.H.Meltzer,Editors 1976,North Holland:Amster-dam:19-46.

[2] F.E.Kydland and E.C.Prescott,"Rules Rather than Discretion The Incon-sistency of Optimal Plans",Journal of Political Economy,1977,85 (3):473-492.

[3] F.E.Kydland and E.C.Prescott,"Time to Build and Aggregate Fluctua-tions",Econometrica,1982,50 (6):1345-1370.

[4] M.Woodford,Interest and Prices:Foundation of a Theory of Monetary Policy 2003,New Jersey:Princeton University Press Princeton.

[5] Christopher A.Sims,"Comparison of Interwar and Postwar Business Cycles:Monetarism Reconsidered",American Economic Review,American Economic Association,1980,vol.70 (2):250-257.

[6] D.Hendry,"Econometrics-alchemy or Science",Economica,1980,47:387-406.

[7] Edward E.Leamer,"Global Sensitivity Results for Generalized Least Squares Estimates",UCLA Economics Working Papers 296,UCLA Department of Economics,1983.

[8] 注意，这种方法并不是严格有效的，因为y作为一个自变量出现在几个方程的右边，但它在整个系统中是内生的。因此，y与方程的残差是相关的，这违背了OLS估计的假设。要进行调整，需要使用某种形式的工具变量或系统估计。

[9] Christopher A.Sims,"Macroeconomics and Reality",Econometrica,Economet-ric Society,1980,vol.48 (1):1-48.

[10] Paolo Giordani,"An Alternative Explanation of the Price Puzzle",Journal of Monetary Economics,Elsevier,2004,vol.51 (6):1271-1296,September.

[11] Soyoung Kim&Nouriel Roubini,"Exchange Rate Anomalies in the Industrial countries:A Solution with a Structural VAR Approach",Journal of Monetary Economics,Elsevier,2000,vol.45 (3):561-586.

[12] Efrem Castelnuovo&Paolo Surico,"Monetary Policy,Inflation Expectations and the Price Puzzle",Economic Journal,Royal Economic Society,2010,vol.120 (549):1262-1283.