干中学模型假定知识来源于物质资本投资 （Arrow，1962^[9]；Romer，1990^[10]），存在无成本的知识外溢。也就是说，单个厂商在投资和生产过程中得到的知识马上可以变成社会公共知识的一部分。

产品生产函数采用柯布道格拉斯生产函数：

各变量定义如下：产量 Y（t）、资本的数量 K（t）、知识的数量A（t）、劳动的数量L（t）、资本占产出的份额α。

模型假定劳动、知识和资本三个存量随时间变动。

s 表示储蓄率，n 表示人口增长率。

当干中学是技术进步之源时，知识积累依赖于传统经济活动产生了多少新知识，依赖于资本的数量。知识作为资本生产的一种副产品而出现时，由于知识的增加量是资本增加量的函数，所以知识存量也是资本存量的函数。因此有：

其中B为转换系数，φ表示知识生产函数的规模报酬。将式 （4-33） 带入 （4-31） 得到：

可见资本的贡献大于其传统贡献：增加的资本不仅通过其对生产的直接贡献来提高产量 ［方程 （4-34） 中的K（t）^α项］，而且通过其间接推动新思想发展从而使所有其他资本更有生产力来提高产量 ［方程 （4-34） 中的K（t）^φ（1-α） 项］。

为分析这一经济的特性，将式 （4-34） 两边求增长率，得到：

从上式可见，无论总产量的增长率，还是人均产量的增长率，都是资本增长率的增函数。

两边同时除以K（t），得到：

g_K的动态学取决于φ的大小。φ决定知识生产函数的规模报酬，知识的生产函数为：

A(λK)=B［λK(t)］^φ =λ^φA

如果φ＞1，A（t） 规模报酬递增；如果φ=1，A（t） 规模报酬不变；如果φ＜1，A（t） 规模报酬递减。依据知识生产函数的规模报酬φ的取值，人均产量增长率具有不同的形态。

1.如果知识生产函数的规模报酬递减 （即φ＜1），人均产量增长率将出现一个稳定性均衡。

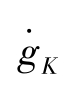的二阶导数为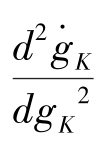：=2（1-α）（φ-1） ＜0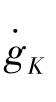，凹向横轴，见图4-15。

图4-15 干中学模型当φ＜1时资本增长率的稳定性均衡

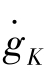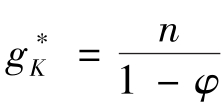在均衡点，=0，，均衡点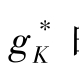的位置，取决于外生变量n、φ。如果外生变量不发生变化，则均衡点的位置也不会发生变化。

由式 （4-37），

如果其他外生变量发生变化，例如储蓄率s 在t₀时点增加，所导致的结果是：g_K 上升，然后t₁时点之后逐渐回到其原来水平，则人均产量的对数lny逐渐移至一条高于原来路径的平行路径。该外生变量s导致的冲击只是短期的增长效应—t₀和t₁之间改变人均产量对数上升的斜率；从长期来看，还是水平效应—t₁之后，人均产量对数上升的斜率恢复到t₀之前的水平，经济增长路径相当于发生了一个向上的平移，如图4-16所示。

图4-16 当φ＜1时，储蓄率上升只有水平效应，没有增长效应(www.daowen.com)

如果外生变量n 或者φ发生变化，则均衡点的位置也相应地发生变化。

如果φ＜1，那么经济的长期增长率是人口增长率n和φ的增函数。当φ＜1时，n 或者φ上升对人均产量的增长率，进而对人均产量的对数带来的影响如图4-17 所示，是一个增长效应。在t₀时点之后，伴随着n 或者φ的上升，人均产量的对数以更陡峭的斜率上升。

图4-17 当φ＜1时，φ或者 n 上升导致的增长路径

2.如果知识生产函数的规模报酬递增 （即φ＞1），人均产量增长率将出现一个非稳定性均衡。

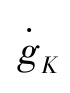的一阶导数为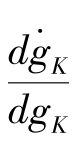：=2（1-α）（φ-1）g_K ＋（1-α）n ＞ 0单调上升。

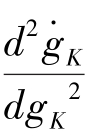的二阶导数为：=2（1-α）（φ-1） ＞0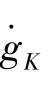，凸向横轴，所以g_K不存在均衡点，随时间不断上升，这意味着一旦开始增长 （这是必然的），就不断增长，并且增长的加速度在不断地上升，如图4-18所示。

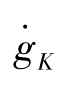由于不存在均衡点，凡是影响g_K 的因素发生变化，g_K 都会相应地发生变化。如果储蓄率上升，不仅导致资本的增长率更快地上升，也会导致人均产量的对数更快地增加，人均产量对数上升的斜率越来越大，有一爆炸性增长，如图4-19 所示。

图4-18 当φ＞1时，资本增长率的非稳定性均衡

图4-19 当φ＞1时，储蓄率上升导致的爆炸性增长

3.如果知识生产函数的规模报酬不变 （即φ=1），人均产量增长率取决于人口的增长率。

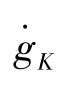的一阶导数为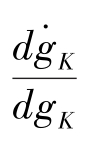：=2（1-α）（φ-1）g_K ＋（1-α）n=（1-α） n

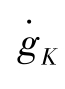的二阶导数为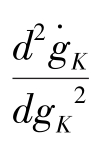：=2（1-α）（φ-1）=0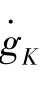，为线性函数。在此情况下，针对人口增长率n 的取值，可具体分析如下两种情况：

（1） 当n＞0时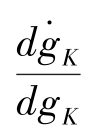，=（1-α）n ＞0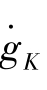，为单调上升的直线，此时g_K不存在均衡点，而是随时间不断上升，类似图4-18所示。由于不存在均衡点，凡是影响g_K 的因素发生变化，g_K 都会相应地发生变化，此时储蓄率s的增长将导致人均产量对数上升的斜率越来越大，出现爆炸性增长，如图4-19所示。

（2） 当n=0时，此时不管g_K 的初始状况如何，g_K 都不变。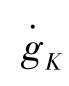=（1-α） ng_K =0，说明横轴上的任一点都可以实现均衡，g_K一旦确定，就不随时间改变，如图4-20 所示。

图4-20 当φ=1且n=0时，储蓄率上升导致的稳定性均衡

把A（t）=BK（t） 代入生产函数式 （4-31），生产函数变为：

资本积累为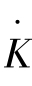：（t）=sY（t）=sbK（t）

这一经济动态学是简单明了的，上述方程直接意味着K稳定地以速率 sb 增长。且由于产量与K成正比，产量也以这一速率增长。在此情况下，长期增长为内生，且取决于储蓄率。如果储蓄率s 上升，则g_K、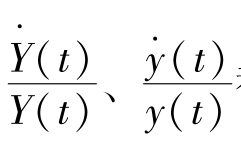都上升，类似图4-17 所示。增加的资本不仅通过其对生产的直接贡献来提高产量 ［生产函数方程中的K（t）^α 项］，而且通过其间接推动新思想发展，从而使所有其他资本更有生产力来提高产量［K（t） ^φ[11]-α）项］，资本的贡献大于其传统贡献。内生增长理论的开创者保罗·罗默 （1986）^[12]将这类模型称为 “Y=AK” 模型 ［式 （4-44）用符号A而不是b］。

干中学模型的主要结论：（1） 如果知识生产函数的规模报酬递减，经济长期增长的源泉取决于人口的增长和提高知识生产函数的规模报酬，储蓄率的上升对经济长期增长只有水平效应，没有增长效应。（2） 如果知识生产函数的规模报酬递增，这就是经济长期不断增长的源泉。一旦开始增长，就会不停地增长。储蓄率的上升、知识生产函数规模报酬的继续增加、人口增长率的提升都对人均产量的增长率起到加速的作用。（3） 如果知识生产函数的规模报酬不变，在人口增长的情况下，知识生产函数规模报酬不变是经济长期增长的源泉，储蓄率的上升、人口增长率的增加对人均产量的增长率起到了加速的作用。在人口不增长的情况下，储蓄率的上升是经济长期增长的源泉。

干中学模型将经济长期增长的源泉归结为：知识生产函数的规模报酬、人口增长率、储蓄率等因素。