在新古典增长理论的框架中，因为资本的边际生产力递减规律决定了资本的净增长上限必然为零，所以资本的边际生产力决定了资本投入量的上限，从而使得均衡增长状态的有效人均资本的增长也等于零。如果能够避免资本边际生产力递减现象出现，则有可能使得均衡增长状态的有效人均资本能够持续增长。AK增长模型对新古典增长模型的关键修正在于将技术因子A看成是经济的内生变量。生产函数是AK函数，则资本的边际生产力不再具有递减现象。琼斯和马努埃利 （1990）^[7]、雷贝洛 （1991）^[8]论证了规模收益不变的生产技术足以保证经济实现内生增长。

对于一个具有AK生产函数的经济体，个体最大化一生效用总和的最优规划问题为：

令效用函数为常相对风险规避型 （Constant Relative Risk A-version，CRRA） u（C（t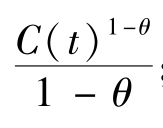））=；θ ＞ 0

ρ为贴现率，θ是相对风险规避系数，定义θ=-Cu″（C）/u′（C）。

为了简化分析，设人口增长率n、折旧率δ与技术进步率g为零。

因为f′（K）=A，资本的边际产品r=A，为常数。依据式（4-25），消费的增长率也是一个常数，这个模型不存在转移动态。

由式 （4-24） 可以得到稳态增长率：(www.daowen.com)

这一模型的储蓄率为：

可见，稳态资本增长率直接成比例于储蓄率。

这意味着，当A-ρ ＞0时，即使没有外生给定的技术进步，经济也可以实现长期增长。

AK增长模型的结论：（1） 资本边际产品A上升，将引起经济增长率的永久性上升，同理，时间偏好参数和风险规避参数的下降也将提高一国经济的长期增长率。参数变动具有长期增长效应。（2） 经济增长没有转移动态，一旦增长持续增长，一旦衰退持续衰退。这样一来无法解释收敛，反而意味着不同经济体收入水平将出现发散。

AK模型揭示了放弃资本收益递减规律如何能够导致内生增长，有助于理解各国收入水平和增长率的巨大差异，但不能解释条件收敛。该模型存在明显的缺陷：一是不能预测绝对收敛或条件收敛，而条件收敛显然是一条经验规律。如果将K仅视为物质资本，那么AK生产函数显然不符合经验规律。不过，如果将K理解为包括人力资本在内的广义资本概念，该生产函数也还大致说得过去。二是AK模型直接放弃资本边际收益递减规律似乎过于突兀。不过，内生增长模型在很大程度上可以归结为AK模型的形式：在这些模型中，虽然在个体水平上存在收益递减，但由于外部性或溢出效应的存在，总量水平上则表现出不变收益或递增收益。AK模型有助于理解这些更重要的模型。