1.k的动态学 （k的微分方程）

与索罗模型一样，k的稳态的条件是实际投资等于持平投资。实际投资为f（k）-c，持平投资为 （n＋g） k （没有考虑折旧）。因此，

当=0时，c=f（k）-（n ＋g） k

根据黄金律规则，当f′（k_Gold）=（n＋g）时，c最大，c随着k的增加，先增加后下降。

再考虑非稳态的情况，当c超过使=0时的水平时，＜0；当c低于使=0时的水平时，＞ 0，见图4-7。

图4-7 k的动态学

2.c的动态学 （c的微分方程）

将r（t）=f′［k（t）］ 代入欧拉方程，得：

当（t）=0时，f′［k^∗（t）］=ρ＋θg

再考虑非稳态的情况，当k＞k^∗时，f′［k（t）］ ＜ρ＋θg，则（t） ＜0；

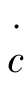当k＜k^∗时，f′［k（t）］ ＞ρ＋θg，则（t） ＞ 0，见图4-8。(www.daowen.com)

图4-8 c的动态学

3.k和c的动态学 （由k和c的微分方程组和横截面条件共同构成）

综合图4-7和4-8，得到图4-9所示的相位图：

图4-9 k和c的动态学

图中k^∗＜k_Gold是因为：f′（k_Gold）=（n＋g），f′［k^∗（t）］=ρ＋θg，而收敛条件ρ-n-（1-θ）g＞0，故f′（k_Gold）＜f′［k^∗（t）］，因此k^∗＜k_Gold。

在拉姆齐模型中，人均资本存量k收敛于k^∗，且低于索罗模型中的黄金资本存量k^∗，因此k^∗被称作 “修正的黄金资本存量”。通过相位图可以证明当k（0） ＞k_Gold时，追求跨期最优化的家庭将降低储蓄，使k收敛于k^∗，且k^∗＜k_Gold。因此，拉姆齐模型表明在索罗模型中高于黄金资本存量的平衡增长路径是不可能的。

4.鞍点路径 （或稳定臂）

根据相位图描绘在 （c，k） 空间上从初始值 （c₀，k₀） 的动态调整轨迹，然后在动态轨迹中排除会使最终资本存量为负和超过资本黄金存量的轨迹，得到鞍点路径 （或稳定臂）。因为：最终资本存量必须为正；超过资本黄金存量会使e^-R（v）e^（n＋g）vk（v） 发散，即家庭收入的现值无穷大于消费的现值，这与家庭效用最大化的目标不一致。

图4-10 鞍点路径

因此，鞍点路径满足家庭的跨期消费最优化、资本存量的稳态、资本存量非负和家庭预算约束的要求。对于任意k₀ ，c₀必须等于鞍点路径上的相应值，并沿着鞍点路径收敛到均衡点E。