假定家庭总人口为L，以速率n增长，L（t）=L（0）e^nt；家庭的个数为H，每个家庭有L/H个人；每个家庭成员在每一时点上提供1单位劳动；资本最初存量为K（0），每个家庭初始资本存量为K（0）/H。

定义家庭效用函数 （也称作 “幸福函数”） 为：

其中，C（t） 为每个家庭成员的消费，u（·） 为即期效用函数，ρ为贴现率 （ρ越大，表明与现期消费相比，远期消费的价值就越低）。

注意：e^-ρt u［C（t）］表示将第t期的消费的效用按照ρ贴现到第0期，即u［C（t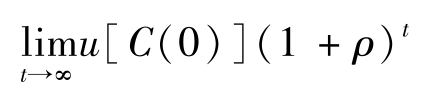）］==u［C（0）］e^ρt 。

选择即期效用函数的形式为：

该函数具有以下四个特点：

（1） 边际效用弹性不变，为-θ。

（2） 跨期替代弹性不变，为1/θ （证明见本讲附录），表示相对风险回避系数不变。常数替代弹性意味着与C无关，因此在消费选择上没有不确定性。但θ决定了家庭在不同时期转换消费的愿望，θ越小，家庭越愿意接受消费较大的波动。

（3） 边际效用u′（C）为正；当θ＜1时，边际效用随C增加而增加，当θ＞1时，边际效用随C增加而减少。

（4） ρ-n-（1-θ）g ＞0是为保证效用不发散 （受到约束）。

第一，考虑劳动增进型的技术进步，并定义每单位有效劳动的平均消费为c（t），有：

Z(t)=Z(0)e^gt

C(t)=Z(t) c(t)

［注意：家庭总消费C（t） L（t）/H=c（t） Z（t） L（t）/H］

代入即期效用函数得：

再代入家庭效用函数，得：

家庭面临的预算约束：其一生消费的现值不能超过其初始财富加上一生的收入 （利息r和工资w，均为外生变量）。

定义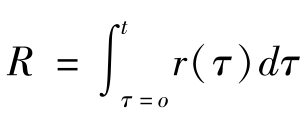，因此在0期投资的1单位产品，在t期产生e^R（t） 单位的产品，它说明在期间 ［0，t］ 上连续以复利计算利息的结果。e^-R（t） 为现值因子。当r不变为-r时，则R=-rt。

家庭t期的劳动收入为w（t） Z（t） L（t）/H，消费支出是C（t） L（t）/H，则家庭的跨期预算约束为：

第二，考虑劳动增进型的技术进步，并定义每单位有效劳动的平均消费为 c （t） 和每单位有效劳动的初始平均资本 k （0），类似的有：

Z(t)=Z(0)e^gt

C(t)=Z(t) c(t)

K(0)=k(0)Z(0)L(0)

代入 （4-11） 得：

再考虑有效劳动的增长，Z（t）L（t）=Z（0）L（0）e^（n＋g）t ，(www.daowen.com)

代入 （4-12），并在两边消去Z（0）L（0）/H，得：

利用家庭资本持有量的极限形式来表示预算约束 （等价命题）。

已知

故

将积分改写成为极限形式，有：

定义第v期的家庭资本持有量的总和为：

式 （4-15） 右边第一项表示第v期的初始资本存量的贡献（非负），第二项表示两期之间的储蓄贡献 （可正可负）。

整理有：

代入极限形式的预算约束式 （4-14） 得：

非负。

由于K（v）=e^（n＋g）vk（v）

根据前面的推导已知家庭的最大化目标函数 （幸福函数）：

跨期预算约束：

（均从有效劳动的人均情况来考虑）

因此可以构造拉格朗日函数：

求解最优的c （t） 使Ω最大，对c （t） 求导数，得到一阶条件为：

两边取对数得：

lnB-βt-θlnc(t)=lnλ-R(t) ＋(n ＋g) t

两边再对t求导数，有：

因此，

这就是描述c调整路径的 “欧拉方程”，它表明家庭可以在不改变一生支出的现值的情况下通过调整其消费增加一生的效用。

对欧拉方程的理解：

已知，C（t）=c（t） Z（t）

因此，当r（t） ＞ ρ时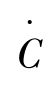，（t） ＞0；当r（t） ＜ ρ时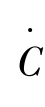，（t） ＜0；θ越小，C的变化率越大。