网络设计通常有几个阶段，包括供应商、生产工厂、仓库和市场的布置，还可能涉及像联合中心和转运点之类的中介设施。一个典型的供应链网络通常如图6-8所示。

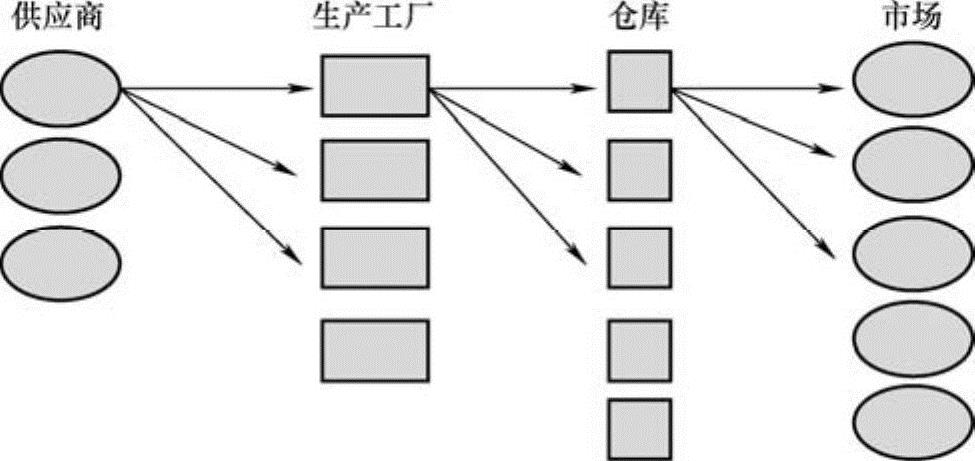
图6-8 典型的供应链网络示意图

除了进行设施布局以外，管理者还需考虑市场在仓库之间的划分以及仓库在工厂之间的分配。配置决策将随着不同的成本变化和市场发展而进行有规则的调整。进行网络设计时，区位决策和配置决策是联合进行的。

每一设施中都将发生与设施、运输和库存相关的固定成本和可变成本。固定成本是指与产量和货运量无关的成本耗费。可变成本则是指在给定设施中那些与产量和运量成比例变化的成本耗费。可变成本、运费和库存成本通常具有规模经济，随着工厂产量的上升，边际成本将会下降。但在网络优化模型中，假设所有可变成本随产量或运量线性变化，即不考虑规模经济。

以两家生产光缆通信设施的厂商为例说明网络优化模型。吉百利（TelecomOne）公司和哈奥普蒂克（Highoptic）公司都是新一代通信设备制造商。吉百利公司着眼于美国东部的市场，它在巴尔的摩（B）、孟菲斯（M）和堪萨斯州的威奇托（W）都有自己的生产工厂，服务的市场包括亚特兰大、波士顿和芝加哥。哈奥普蒂克公司瞄准美国西部的市场，服务的市场包括丹佛、内布拉斯加州的奥马哈和俄勒冈州的波特兰，其几个生产工厂分别位于怀俄明州的夏延（C）和犹他州的盐湖城（S）。

工厂的生产能力、市场需求、每1000单位产量的生产成本和运输成本以及每个工厂每月的固定成本如表6-5所示。

表6-5 吉百利公司和哈奥普蒂克公司的生产能力、市场需求和成本

（续）

1.需求量在工厂之间的分配

从表6-4中可以看到：吉百利公司每月的总生产能力为71000单位，总需求量为32000单位；而哈奥普蒂克公司每月的生产能力为51000单位，总需求量为24000单位。两个公司都必须考虑在工厂之间进行需求分配。随着成本和需求的变化，这种分配决策每年都要进行调整。

需求分配问题可以用网络优化模型解决。这一模型需要输入以下数据：

n：工厂的数目。

m：市场或需求地的数量。

D_j：市场j的年需求量。

K_i：工厂i的年生产能力。

C_ij：工厂i生产一单位产品并送到市场j的成本（包括生产、库存和运输成本）。

向不同工厂分配不同市场和需求的目标是使设施成本、运输成本和库存成本之和最小。对决策变量作如下定义：

x_ij：每年从i工厂到市场j的运量。

这一问题构成了下面这一线性模型

限制条件为

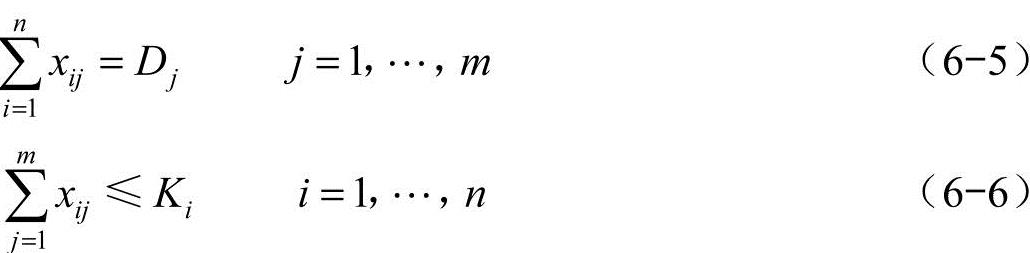
式（6-5）的限制保证了每一市场的需求得以满足：而式（6-6）的限制则确保了每一工厂不会超过其生产能力进行生产。

对这两家公司来说，可以运用Excel软件中的Solver工具进行市场分配。表6-6给出了最优需求配置方案。

表6-6 吉百利公司和哈奥普蒂克公司的最优需求配置

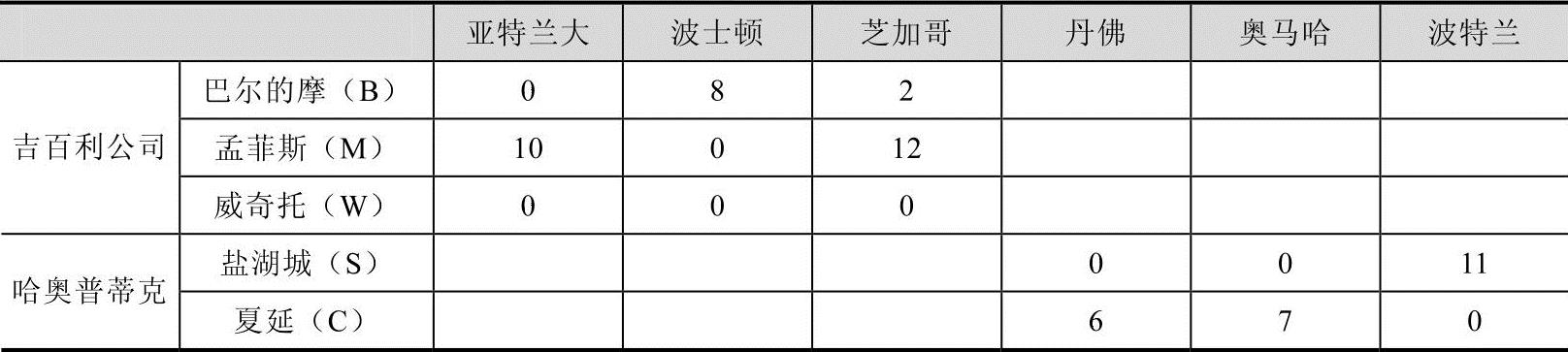
我们注意到，虽然威奇托是最佳工厂区位，且吉百利公司位于威奇托的工厂可以运营，但该工厂却已停止生产。表6-5给出的需求分配表明，吉百利每月消耗的可变成本是14886000美元，月固定成本为1395000美元，月总成本为28836000美元；哈奥普蒂克公司的月可变成本力12865000美元，月固定成本为8500000美元，月总成本为21365000美元。

2.工厂布局：生产能力既定的工厂布局模型

吉百利公司和奥普蒂克公司的经理们已经决定将这两家公司合并成为一个名为吉百利奥普蒂克的新公司。他们认为，如果将两个供应网络恰当地合并，将受益匪浅。新公司将拥有5个生产厂，服务于6个市场。管理者正在讨论是否每个工厂都是必需的。他们已经指派了一个供应链小组来研究供应网络，以明确哪些工厂应当关闭。

供应链小组决定使用布局的网络优化模型来解决这一问题。这一模型需要输入以下数据。

n：潜在的工厂布局区位数量。

m：市场或需求点的总数量。

D_j：市场j的年需求量。

K_i：工厂i的潜在年生产能力。

F_i：工厂i运营中按年分摊的固定成本。

C_ij：工厂i生产一单位产品并将之送到市场j的成本（包括生产成本）。

该小组的目标是决定工厂的区位，然后将市场需求分配到每一个正在营运的工厂中去，以减少设施成本、运输成本和库存成本。决策变量的定义如下：

y_i=1 如果工厂i运营，否则为0。

x_ij：每年从工厂i送至市场j的货物数量。

然后，这一问题构成以下整数模型

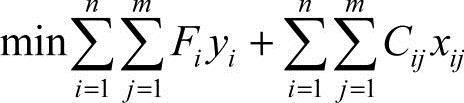
限制条件为

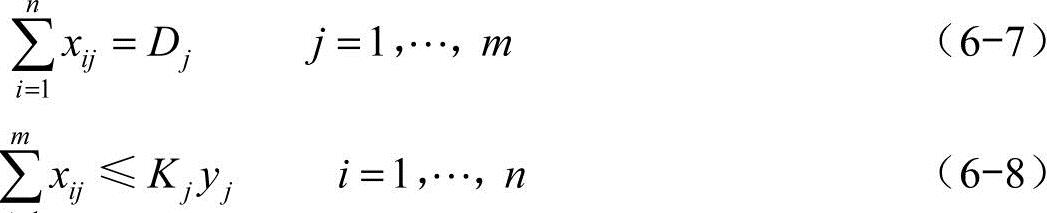
y_i∈{0，1} i=1，…，n （6-9）

目标方程是使得网络建设和运营总成本（包括固定成本和可变成本）最小化。式（6-7）的限制条件保证了所有需求得到满足；式（6-8）确保了每一工厂的生产不超过其生产能力（显然，如果工厂被关闭，则生产能力为0；如果工厂运营，则生产能力为K_i，K_iy_i恰当地表明了这一点）；式（6-9）的限制条件将工厂分为运营（y_i=1）和关闭（y_i=0）两类。这一解决方案将明确哪些工厂继续运营，并将市场需求划分到这些工厂中去。

合并后的新公司的生产能力和需求资料，以及生产、运输和库存费用如表6-4所示。供应链小组决定用Excel软件中的Solver工具求解工厂区位模型。

建立Solver模型的第一步是输入成本、需求和生产能力的有关信息。将5个工厂的固定成本输入B4～B8这几个方格中，生产能力输入列I4～I8几个方格中去，可变成本C_ij输入到C4～H8这个长方形区域的所有方格中。6个市场的需求量则位于C4～H8这几个方格。接下来每个决策变量对应于一个方格，如图6-9所示。每一变量的初始值均为0。方格B12～B16代表决策变量y_i，C12～H16这个长方形区域中的方格代表决策变量x_ij。

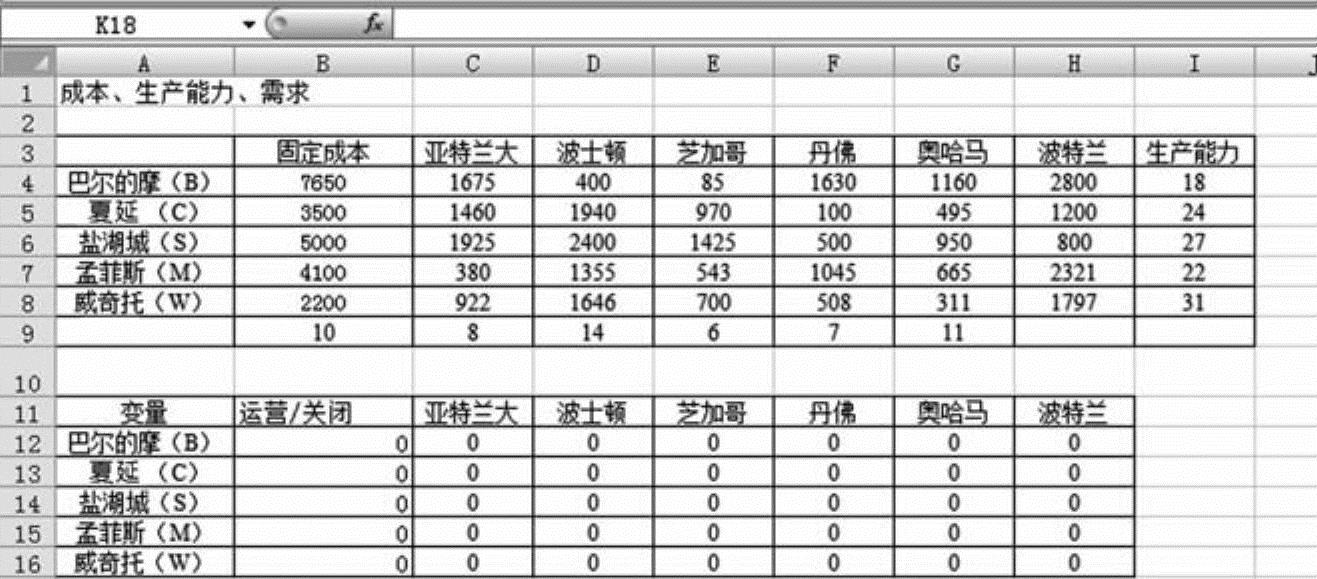
图6-9 决策变量的分布

下一步要根据式（6-7）和式（6-8）给出的限制条件找到合适的位置。限制条件方格如图6-10所示。I4～I8行表明式（6-8）的生产能力的限制；而方格C24～H24表示式（6-7）的需求的限制。例如，I4的限制条件对应巴尔的摩（B）工厂的生产能力的限制；方格C24对应亚特兰大市场的需求量的限制。计算限制条件方格所示值的不同公式如表6-7所示。生产能力限制要求方格所示值大于等于0，而市场需求限制条件则要求方格所示值等于0。

图6-10 限制条件的分布

表6-7 限制条件方格的计算公式(www.daowen.com)

接下来建立目标模型的方格，用目标模型计算供应网络中总的固定成本和可变成本。在这种情形下，目标模型是固定成本加上网络运行的可变成本。目标模型方格位于B24，包含以下公式

=总产量（C4：H8，C12：H16）+总产量（B4：B8，B12：B16）

下一步是使用Tools/Solver来激活Solver。在Solver的特色对话框中输入以下表示工厂区位的信息：

设计目标格：B24

等于：选择“MIN”（最小化）

通过改变单元格：B12：H16

限制条件：B12：H16≥0（所有决策变量非负）

B12：B16二进位法（所有区位变量y都是二进位制的，即取值只能是0或1）

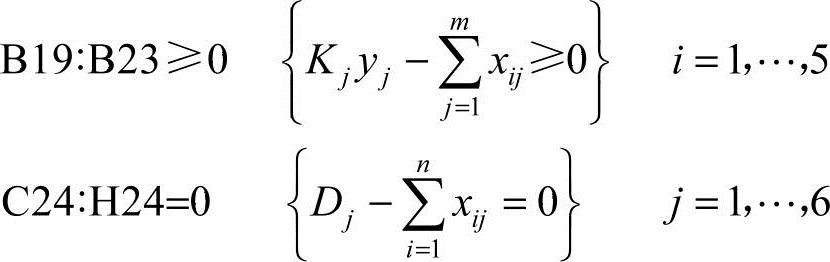
在Solve的对话框中单击“Options”（选择），然后选定“假定线性模型”（这一选定显著地加快了解决问题的速度）。回到特色对话框，单击“Solver”求解最佳解决方案，就返回到变量区域，如图6-11所示。

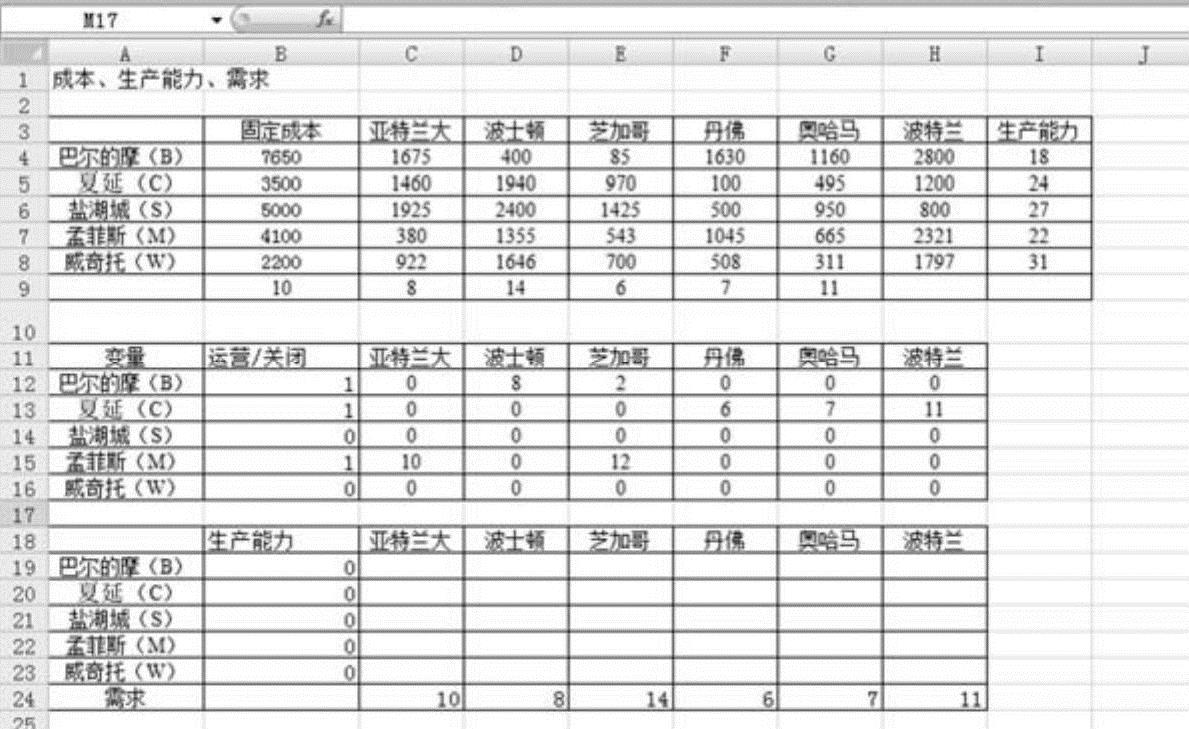
图6-11 吉百利奥普蒂克公司的最优网络设计

根据图6-11，供应链小组得出结论：最佳选择是关闭在盐湖城和威奇托两地的工厂，而继续运行在巴尔的摩、夏延和孟菲斯的工厂。每月的网络和运营成本为47401000美元。这一成本比吉百利公司和哈奥普蒂克公司独立运营时的成本节省了近3000000美元。

3.工厂布局：既定生产能力的工厂布局模型——单个供应源模型

在某些情形下，企业要设计这样的供应链网络：在这个网络中，只有一个工厂为一个市场服务。这时这个工厂被称为单个供应源。企业可能强加上这一限制条件，因为这样就减少了网络协调的复杂性，而且对每一设施的灵活性要求也会降低。为了适应这一限制，必须对前面讨论过的工厂区位模型作一些修改。

决策变量的定义改为

y_i=1 如果工厂在点i布局，否则为0。

x_ij=1 如果市场j由i提供产品。

于是，这一问题构造了以下整数模型

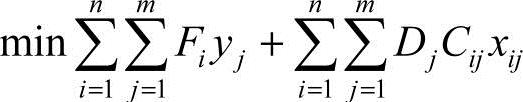
限制条件为

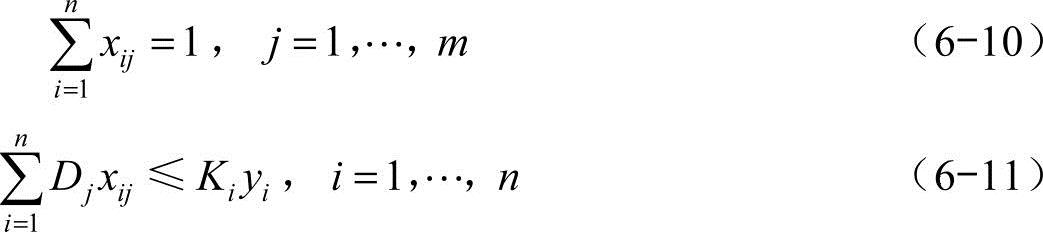
x_ij，y_i∈{0，1} （6^-12）

式（6-10）和式（6-11）表明某一市场只能由一个工厂提供产品。式（6-12）的限制条件将工厂分为运营（y_i=1）或关闭（y_i=0）两类。

如果每一个市场只由一家工厂提供产品，那么，前面讨论的合并后的吉百利奥普蒂克公司将有可能选择一个最佳供应链网络。用表6-4中的资料，供应链小组利用单个供应源模型求解最优的网络设计，如表6-8所示。

表6-8 单个供应源下吉百利奥普蒂克公司的最优网络架构

如果是单个供应源，吉百利奥普蒂克的最优选择是关闭在巴尔的摩和夏延的工厂，这与图6-11给出的结果不同，图6-11要求关闭的是盐湖城和威奇托的工厂，这是因为图6-11中的网络设计没有单个供应源这一限制。因此，供应链小组得出结论：单个供应源在使协调简单、灵活性要求降低的同时，却使网络的月运营成本增加了23160000美元。

4.工厂和仓库同时布局

如果要设计从供应商到顾客的整个供应链网络，就要考虑更一般的工厂布局模型了。来看这样一个供应链网络：供应商向工厂提供原材料，工厂设有为市场服务的仓库，必须为工厂和仓库同时作出布局和容量配置决策，使大量的仓库用于满足市场，大量的工厂用于更新库存。在这一模型中，同样对计算单位进行了调整，使得来自供应商的每一单位的投入，能生产出一单位的最终产品。这一模型要求输入以下数据：

m：市场或需求点的数量。

n：潜在的工厂区位数量。

l：供应商的数量。

t：潜在的仓库区位数量。

D_i=客户i的年需求量。

K_i=布局于i点的工厂的生产能力。

S_h=供应商h的年供应能力。

W_e=布局于e点的仓库的年仓储能力。

F_i=布局于i点的工厂的年固定成本。

F_e=在e地点布局一家仓库的年固定成本。

C_hi=从供应源h运送单位货物到工厂的i的成本。

C_ie=i点的工厂生产单位产品并运送到e点的仓库的成本。

C_ej=从e点的仓库给i点的顾客运送单位货物的成本。

这一模型的目标是确定工厂和仓库的区位以及不同地点之间的运输数量，以减少总的固定成本和可变成本。定义如下决策变量：

y_i=1如果工厂布局在i点，否则为0。

y_e=1如果仓库布局在e点，否则为0。

x_ej=每年从e点的仓库运送到市场i的货物的数量。

x_ie=每年从i点的工厂运送到e点的仓库的货物数量。

x_hi=每年从供应商h运到i点的工厂的原材料数量。

于是，这一问题构建了以下整数模型

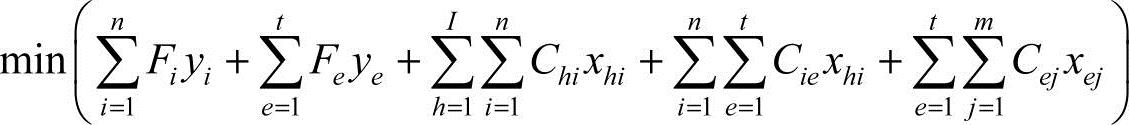
限制条件为

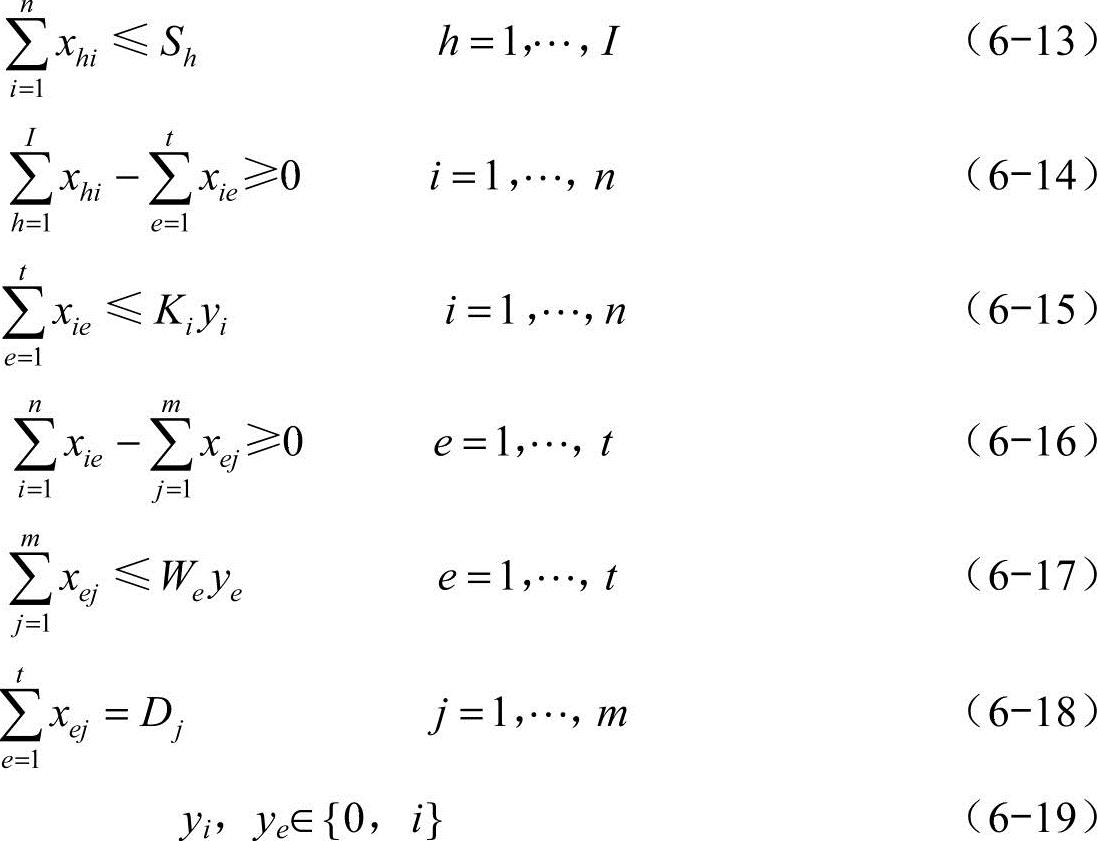
目标模型是使总的固定成本和可变成本最小。式（6-13）的条件限制表明，从供应商运到工厂的原材料不能超过供应商的生产能力；式（6-14）的限制条件表明，工厂运出货物的数量不能大于原材料的输入量；式（6-15）的限制条件表明，工厂的产量不能超过其生产能力；式（6-16）的限制条件表明，仓库的发货量不能超过来工厂的货物总量；式（6-17）的限制条件说明，经过仓库的货物总量不能超过其仓库容量；式（6-18）的限制条件说明，所有的客户需求都将得到满足；式（6-19）的限制条件表明，工厂要么关闭，要么运营。