重力区位模型用于选择这样一些区位：该区位能使从供应商处运来原材料的运输成本和向市场运送最终产品的运输成本之和最小。重力区位模型假定无论是市场还是供应源都可以在坐标系中用点表示出来，所有两点之间的距离都可以像坐标系中两点之间的距离一样计算出来。而且假定运费随着运量的增加呈线性增加。运用重力区位模型来为某一生产厂选择区位，这一生产厂从原材料处获得原材料供应，并向市场运送最终产品。这一模型要求输入以下数据：

x_n，y_n：市场或供应源n的横、纵坐标。

F_n：在供应源n或市场与工厂之间每单位货物每英里的运输成本。

D_n：供应源或市场与工厂之间的运量。

如果（x，y）是为工厂选定的位置，则在点（x，y）布局的工厂与供应源n的距离为

因而，总运输成本TC可表示为

通过循环进行以下三步，就可以得到总运输成本TC最小的区位。工厂的坐标（x，y）是进行每一循环的出发点：

（1）利用式（6-1）计算工厂到每一供应源或市场的距离d_n；

（2）为工厂求得一个新的区位（x'，y'），其中

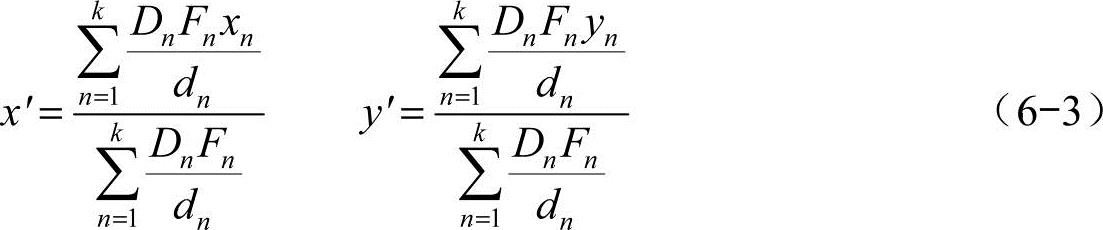(www.daowen.com)

（3）如果新区位（x'，y'）与原有区位（x，y）几乎相同，则停止运算。否则，设（x，y）=（x'，y'），重新从第一步开始。

下面用钢铁设备（Steel Appliances）公司的例子来说明这一程序。钢铁设备公司是一家高质量的冰箱和厨房用具的生产商，它在丹佛附近有一个装配厂。该装配厂的生产能满足全美国的市场需求。由于市场需求迅速增长，这家公司的首席执行官决定建立另一个工厂，以满足东部市场的需求。首席执行官要求供应链管理者为新的工厂选择一个合适的区位。三个配件厂分别位于纽约州的布法罗、田纳西州的孟菲斯和密苏里州的圣路易斯，它们将向新工厂提供配件。新工厂将为亚特兰大、波士顿、杰克逊维尔、费城和纽约的市场提供产品。表6-3给出每一个区位的坐标、每一个市场的需求量、从每一个配件厂的进货以及供应源或市场到工厂的运费情况。

表6-3 钢铁设备公司的供应源和市场区位

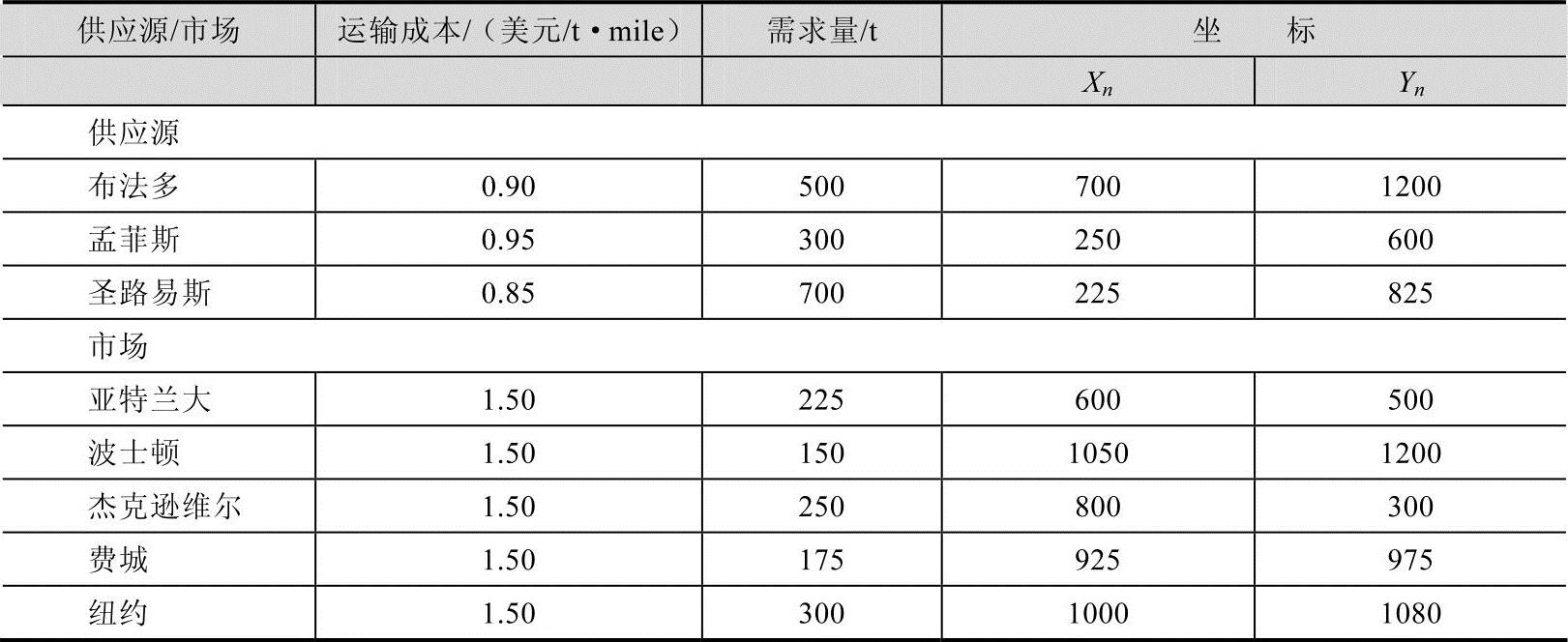
供应链管理者决定使用上面提到的循环程序进行工厂区位决策。他挑选的工厂的初始位置是（0，0），第一轮循环分析如表6-4所示。

表6-4 对钢铁设备公司进行分析的第一轮循环

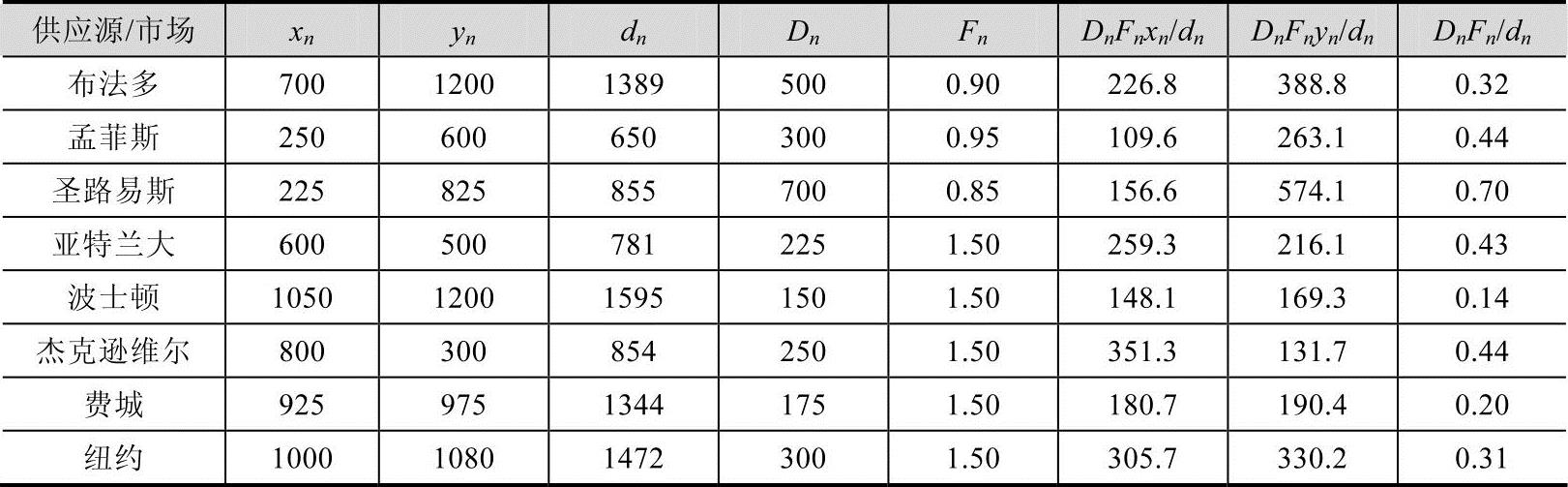
依据式（6-3）和表6-4的分析，管理者得到如下结果

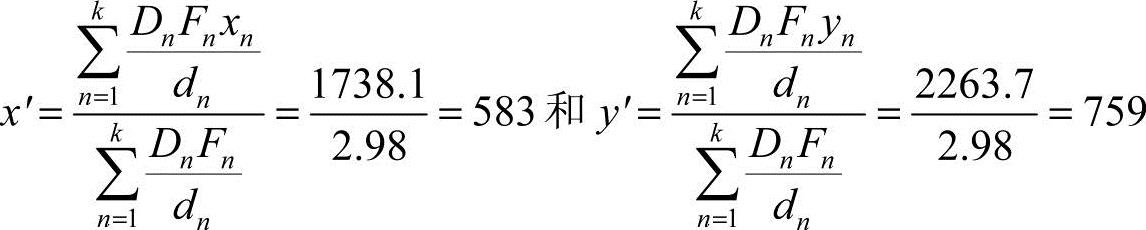
第一轮循环后，（x，y）=（0，0）≠（x'，y'）=（583，759）。因此，管理者假定（x，y）=（583，759），并进行新一轮的循环，重复第一至三步。经过40次这样的循环，管理者得到了（x，y）=（681，882）这一结果。重复进行第一至三步，结果是（x'，y'）=（681，882）。由此，管理者确认坐标点（x，y）=（681，882）是使总运费最小的工厂区位。从地图上可以看出，这一坐标点的位置靠近加利佛尼亚州北部与弗吉尼亚州交界处。重力区位模型得出的最佳区位也许在实际中并不可行，但可以寻找一个接近这一模型结果的位置，管理者就可以将工厂布局于此——公司的运费最低点。