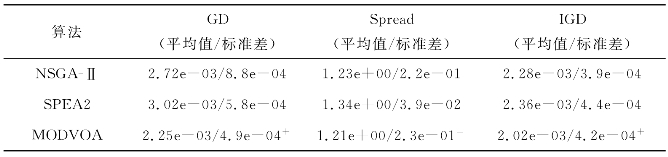
为了验证MODVOA在求解加工时间可控的柔性作业车间调度问题上的优越性，我们将NSGA-Ⅱ、SPEA2及MODVOA三种算法进行对比。各算法的参数设置与前述章节保持一致，每种算法在该问题上分别进行了30次独立运算，并获得了相关性能指标（收敛性能指标GD、分布性能指标Spread以及综合性能指标IGD）的结果。表8-11展示了不同算法在该问题上独立运算30次获得的各性能指标的统计结果（平均值和标准差）。从表中可知：对于收敛性能指标GD和综合性能指标IGD，MODVOA显著优于其他算法；同时，在分布性能指标上，MODVOA相比于其他算法也是具有一定竞争力的。这表明MODVOA非常适合求解这类调度问题。因此，本书采用了MODVOA算法来优化发动机冷却风扇生产车间调度问题实例。

表8-11　NSGA-Ⅱ、SPEA2和MODVOA获得的各性能指标的平均值及标准差

(www.daowen.com)

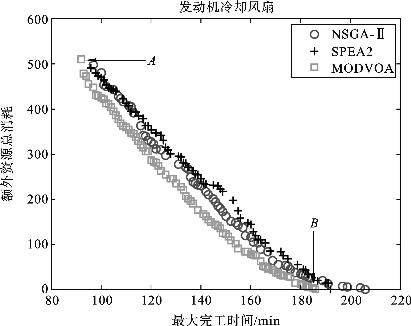
图8-6　不同算法获得的Pareto前端

图8-6展示了不同算法获得的Pareto前端。对于收敛性能和分布性能来说，MODVOA明显优于其他算法。MODVOA具有良好性能的原因在于其复制策略和改进的探索机制。首先，采用复制策略有助于提高算法搜索的多样性。因为强病毒和普通病毒有不同的搜索方向，强病毒主要负责改善非支配解的质量，而普通病毒主要负责探索未知解区域，所以，普通病毒产生的下一代种群具有良好的多样性。但NSGA-Ⅱ和SPEA2没有包含这种复制策略，这两种算法均采用了同一种搜索算子来更新种群，这不利于提高种群的多样性。其次，为了确保良好的收敛性，MODVOA采用了一种改进的探索寻优机制，该机制可扩展加工时间来填充闲置时间，从而进一步提高解的质量。利用这个问题属性，算法可以指导解的搜索方向朝着最优Pareto解集的区域前进，而NSGA-Ⅱ和SPEA2却没有采用启发式信息来改善生产系统的整体性能。从图8-6可知，目标最大完工时间和额外资源总消耗是相互冲突的。例如，A点的最大完工时间是最小的（即92），而在此处的另外一目标额外资源总消耗是最大的（即510）。相反，B点的额外资源总消耗最小（即0），而在此处的最大完工时间是最大的（即186）。根据不同的实际需求，决策者可以选择一个合适的解方案。例如，如果一个用户更看重最大完工时间指标，则对应的偏好解在A点区域附近，反之同理。图8-7展示了仅考虑最大完工时间指标最小情况下的甘特图。

图8-7　A点对应的生产调度甘特图