正如前所述，提出的算法包含两个主要改进策略：①种群初始化策略；②改进的局部寻优机制。下面分别探讨这两种策略的有效性，并对参数B进行灵敏度分析实验。

7.4.3.1　种群初始化策略性能评价分析

在该实验中，我们测试了MODVOA算法与其变种算法的性能，其中MODVOA1表示带有随机初始化的MODVOA，而MODVOA本身含有改进的种群初始化策略。本实验对MODVOA和MODVOA1进行了对比分析，验证了种群初始化策略的有效性。表7-3记录了两种算法在30个问题上独立运行30次的统计结果。

表7-3　MODVOA1和MODVOA获得的各性能指标的平均值和标准差

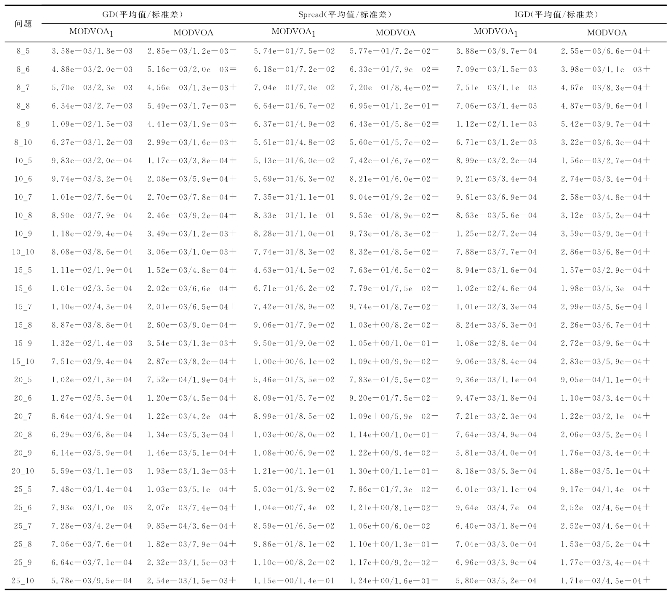
从表7-3中可看出，对于性能指标GD和IGD而言，MODVOA在大多数问题上显著优于MODVOA1。这表明改进的种群初始化策略可明显地提高解的质量，其原因在于这种策略有助于候选解在早期收敛到潜在的Pareto最优解集。对于分布性指标，在大多数问题上，MODVOA1显著优于MODVOA，这表明随机初始化的种群很可能分布在不同的搜索空间中，随机初始化有助于提高种群的多样性。总的来说，就综合性能IGD而言，MODVOA在多数问题上优于MODVOA1，尽管MODVOA的分布性能（多样性）较差，但它在收敛性能以及扩展性能方面优于其他算法。因此，可以说改进的种群初始化策略有益于算法性能的提升，并能获得良好的结果。

7.4.3.2　基于问题属性的改进的局部寻优机制性能评价分析

为了验证改进的局部寻优机制的重要性，本实验对比了MODVOA与无该机制的MODVOA（记为MODVOA2）算法的性能。它们均采用了与7.4.2小节中一样的参数设置。对于MODVOA，参数B设置为2。表7-4展示了两种算法在30个问题上独立运行30次的统计结果。(www.daowen.com)

表7-4　MODVOA2和MODVOA获得的各性能指标的平均值和标准差

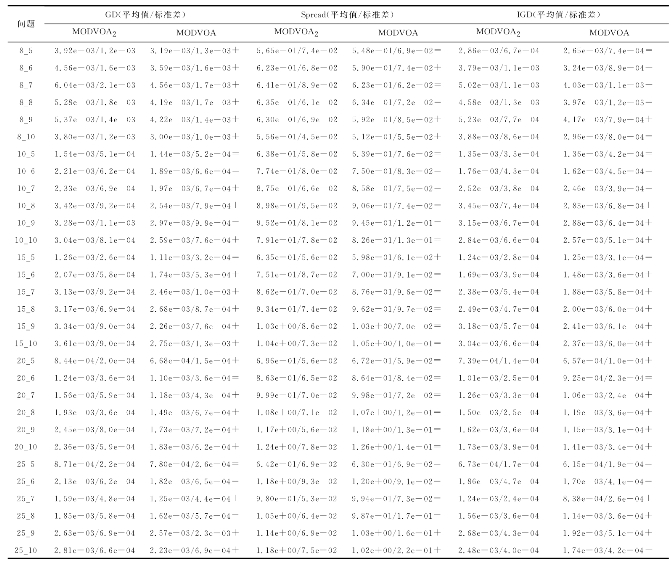
从表7-4中可以看出，就GD性能指标而言，在大多数问题上MODVOA明显优于MODVOA2。同时，对于综合性能指标IGD，MODVOA在大多数问题上要强于MODVOA2，具体说来，MODVOA在20个问题上具有显著的优越性。在分布性指标方面，MODVOA在19个问题上优于MODVOA2，其中在6个问题上具有显著的优越性。这表明对于分布性能指标，MODVOA和MODVOA2之间不存在显著差异。但是总的来讲，对于GD和IGD指标，MODVOA要强于MODVOA2。MODVAO具有优越性能的原因在于其改进的局部寻优机制。这种机制很好地利用了加工时间可控的特点，加工时间的可控性也许为寻找一个潜在优良解提供了额外的灵活性，这有助于提高生产系统的整体性能。

基于以上实验结果的对比，可以得出MODVOA明显优于MODVOA2，这进一步证实了改进局部寻优策略的有效性。算法的优越性能可能归因于改进复制操作和局部寻优机制的混合策略，通过这些策略来保持搜索的多样性和开采性能的平衡。

图7-6　参数B的灵敏度研究

7.4.3.3　控制参数B的灵敏度研究

在改进的局部寻优机制中，参数B控制着搜索过程中的局部寻优机制，本小节探讨了参数B对算法性能的影响。除了参数B外，其他参数设置与7.4.2小节中参数设置一样。具体地，B是一个以1为步长、从2到8逐渐递增的数。在该实验中，仅采用综合性能指标IGD来评价不同算法的性能，这些统计结果通过箱形图直观地展示出来。由于空间有限，不可能展示所有问题的图形，因此，选取了三个不同水平问题的箱形图来说明参数B的作用。图7-6描绘了30次独立运算的统计结果的分布情况，其中圆圈表示IGD的平均值，图中的纵坐标表示IGD值，横坐标表示参数B的取值范围。从图中可看出，随着参数B的增加，三个问题的IGD值均保持相对稳定的变化趋势，也就是说，所提出的算法在求解该问题时对参数B不是特别敏感。根据以上参数实验，可得出改进的局部寻优机制对算法有正面的影响，但相关参数对问题的性能不敏感。在本书中，B值为2。