正如前所述，原始的更新探索机制无法求解多目标优化问题。为了解决这个问题，本章提出了一种基于具体问题特性的局部搜索机制。通常加工时间越短，最大完工时间也就越短，但是机器很可能处于闲置阶段，这将导致额外资源的浪费。通过减少资源的消耗而延长某些工件的加工时间，最终可减少闲置时间，也就是加工时间的可控性可以缩短机器的闲置时间。因此，在不影响最大完工时间指标的情况下，适当地延长加工时间，可消除闲置时间以减少额外资源的浪费。即这个策略不需要改变工序的顺序（数据结构o）就可在减少额外资源消耗的同时保持最大完工时间不变。这个策略主要集中在搜索的后期，引入参数B控制探索搜索机制。本章也研究了该问题的属性特点，以便在搜索的后期获得非支配解。在介绍问题属性之前，提出以下合理的假设。

假设：当一个工序操作Oij（i=1，2，…，n；j∈ni）在机器k∈Mij上以较快速度加工时，其加工时间会缩短，但额外资源消耗会增加。换句话说，某道工序在不同性能或者不同速度机器上进行加工时，将会有不同的实际加工时间和额外资源消耗。详细地讲，每道工序要么在环境1（较慢速度）下加工，要么在环境2（较快速度）下进行加工，因此有

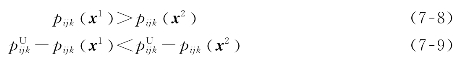
依据上面的假设，问题的具体属性如下。

属性：如果在相同的工序顺序和机器分配情况下，保持最大完工时间目标不变，若解x1=（o1，u1，v1）的总加工时间比解x2=（o2，u2，v2）的总加工时间大，则解x1支配解x2。也就是说，若满足Cmax（x1）=Cmax（x2）且TC（x1）＜TC（x2），则x1＜x2。

证明：t（xr）表示解xr（r=1，2）在所有机器上的总实际加工时间，其计算公式为

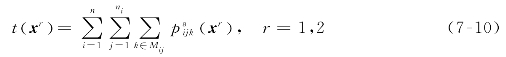
因为x1有一个较大总加工时间，其两个解的最大完工时间是相同的，于是有

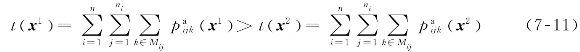
每道工序加工时间的上界已给出且是固定的，也就是因此有(www.daowen.com)

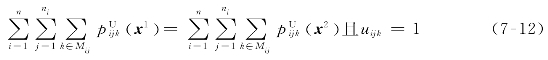
即TC（x1）＜TC（x2）。因为Cmax（x1）=Cmax （x2），则可推导出x1＜x2。

根据问题属性，当调度方案给出后，最大完工时间目标也被相应地确定下来。在该固定的最大完工时间目标下，调整某些工序的加工时间以减少额外资源消耗。采用启发式搜索策略，首先计算一个给定工序的闲置时间，然后在其范围内更新相应工序的加工时间，最后，在每台机器上的最后一道工序执行以上相同的操作。算法7-1展示了该操作，同时图7-5给出了一个详细的算法流程。

算法7-1　改进的探索机制（o，u，v）

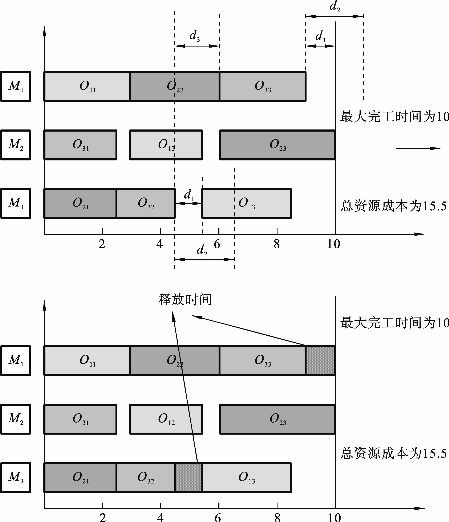
图7-5　基于问题的局部寻优操作流程