本章研究的调度问题可描述如下：n个工件以相同流程方向需要经过m个阶段，每个工件在每个阶段上只有一道工序，加工过程中不允许抢占与中断。多台机器在某时刻可同时加工一个工件。当只有一台机器用来加工相应的工序时，每道工序都有一个正常的加工时间。工序的正常加工时间可通过分配多台机器资源到对应工序上进行压缩，但会引来额外的机器负载或者机器干涉。显然，所研究的调度问题是一类加工时间可控的置换流水车间调度问题的扩展版本。此外，本章所研究的问题比传统的调度问题要复杂得多。该类调度问题的基本特点可总结如下：

（1）加工时间可以通过安排额外的机器到对应工序上进行压缩。

（2）考虑了准备时间，准备时间与相邻两工件的排序相关。

（3）所有工件在每阶段上的释放时间是相对较短的。因此，在该问题中，工件释放时间可被忽略。

（4）考虑了相邻阶段之间的传输时间。传输时间不仅与阶段（站点）之间的距离相关（通常站点的位置是固定的），同时也与所运输的工件相关，因此传输时间是依赖工件的。

（5）当同时考虑准备时间和传输时间时，准备时间与传输时间的叠加是允许的。在这里，只有当先前工序的传输时间和当前工序的准备时间完成后，当前工序才能开始加工，如图5-1所示［13］。

为了建立加工时间可控的多目标流水车间调度问题的数学模型，本章所用到的符号和决策变量如下。

1.符号

j：工件j，j∈J。

n：工件总数。

m：阶段总数。

π：一个可行的排序。

π（j）：在一个排列中第j位置上的工件。

Ci：在阶段i上工件的完工时间。

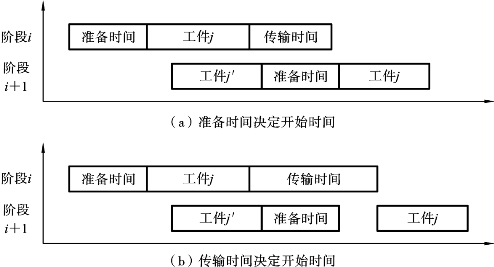
图5-1　准备时间与传输时间叠加

Cmax：最大完工时间，也就是从开始到最后一个工件被运输到仓库的时间。

M：机器集合。

Mi：阶段i上的可用机器集合。

TMi：在阶段i上，加工一个工件可用机器的数目。

Oij：工件j在阶段i上的工序。

Nij：加工工序Oij所用的机器数。(www.daowen.com)

pij：工序Oij的正常加工时间，即对应工序上机器数需满足条件Nij=1。

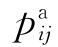：工序Oij的实际加工时间，它与对应工序上的机器数成反比，即

Sij：工序Oij的开始时间。

s Ti0j：在阶段i上最先加工工件j的准备时间。

s Tijj＇：在阶段i上工件j与工件j＇的准备时间。

tjii＇：从阶段i到阶段i＇上工件j的传输时间。

tj0i：工件j从开始仓库到阶段i上的传输时间。

tjiw：工件j从阶段i到结束仓库的传输时间。

ui：第i阶段机器负载惩罚系数。

L：一个无穷大的正数。

2.决策变量

Nij：加工工序Oij所用的机器数。

Sij：工序Oij的开始时间。Sij需满足下面的条件：

根据上面已给出的符号，加工时间可控的多目标流水车间调度问题可被定义成一个多目标数学模型，其公式如下：

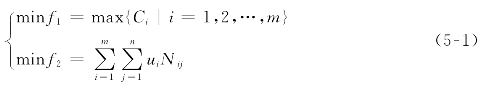
约束条件：

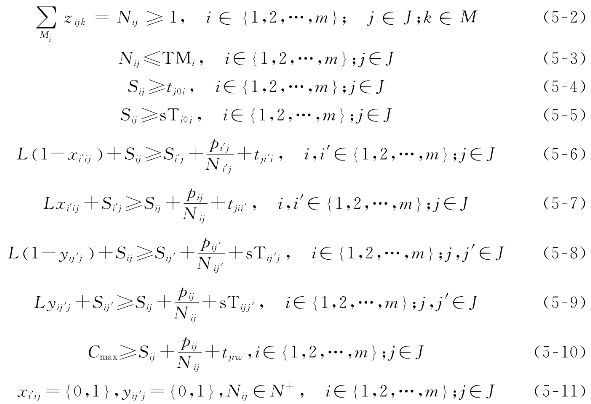
公式（5-1）定义了问题的优化目标是同时最小化最大完工时间和机器负载惩罚量；约束（5-2）确保了在每个阶段上每个工件至少被一台机器加工，该约束不同于传统调度问题中的约束；约束（5-3）保证了每道工序对应的可用机器数在给定的范围内；约束（5-4）确保了只有当工件从开始仓库运输到第一个站点后工件才可被加工；约束（5-5）定义了只有当前工序的准备时间完成后该工序才开始加工；约束（5-6）和约束（5-7）共同确保了只有先前工序完工后工件才开始加工；约束（5-8）和约束（5-9）共同确定了在相同阶段上只有先前工序和其准备时间完成后，当前工件才能进行加工；约束（5-10）定义了最大完工时间等于最后一道工序的完工时间与传输到仓库的时间之和；约束（5-11）限制了决策变量是二元变量，Nij是一个正整数。该数学模型很容易扩展到其他经典调度问题中，如作业车间和组车间调度问题。

显然，该问题的两个目标是相互冲突的，当多台机器同时加工某道工序时，其加工时间是被压缩的，而对应的机器负载或机器干涉将会有所增加。此外，由于该问题具有NP难等特点，大规模调度问题很难通过提出的MIP模型和精确算法在合理的时间内进行求解，因此，本章提出了一种高效的MODGWO算法来求解该类问题。