本书结合GA的强全局搜索能力与VOA的强局部搜索能力，提出了一种基于混合GA-VOA的MODVOA算法来求解并行机调度问题。图4-3展示了MODVOA的基本流程框架，主要包括编码与解码、初始化、复制以及维护等操作。

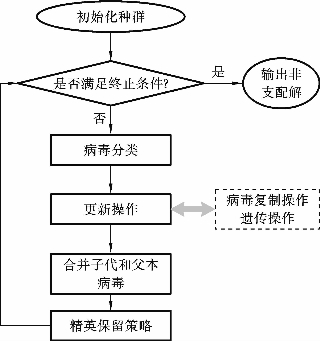
图4-3　基于GA-VOA的MODVOA的基本流程框架

本章的并行机调度问题是一个多目标调度优化问题，而且也是NP难问题，而原始VOA主要用来求解单目标连续优化问题，因此，本章提出了一种基于VOA的多目标离散元启发式算法，用来求解加工时间可控的并行机调度问题，其主要步骤如下。

Step 1：初始化。根据编码机制和种群初始化策略，产生初始病毒。依据最大完工时间和额外资源消耗指标来评价这些病毒种群，并根据快速非支配排序方法对病毒种群进行排序。

Step 2：复制步骤。

Step 2.1：病毒分类。本章所研究问题中病毒分类与单目标问题中病毒分类的步骤不同。本章病毒分类的操作如下。如果病毒种群含有多个非支配层水平（即秩），病毒可以被划分为两大类：非支配解集（强病毒）和支配解集（普通病毒）。否则病毒全是非支配解集。在这种情况下，病毒随机地被划分为强病毒和普通病毒。

Step 2.2：病毒复制。VOA根据强病毒和普通病毒信息可生成新的病毒。因为每个病毒均包含了两层信息，所以采用混合算子来更新病毒的不同部分。

Step 3：更新和维护。

Step 3.1：更新探索机制。这种机制与原始VOA中的更新探索机制不同。在多目标优化问题中，由于一个指标的改善会导致另一个指标的恶化，所以平均适应度的概念不能直接应用在多目标优化问题中。但是，加工时间的可控性为获取高质量解提供了方便，从而改善了生产系统的整体性能。因此，本书利用了问题的属性来加强算法的寻优探索机制。

Step 3.2：种群维护机制。该机制基于公式（4-14）和精英保留策略［4］，被淘汰的病毒数不是动态变化的，而是一个固定的常数。种群大小为N的父本种群Pt和相同大小的子代种群Qt合并为一个大小为2N的混合种群Rt。然后评价混合种群Rt，并根据非支配排序和拥挤距离技术，选择出前N个较好的个体作为下一次迭代更新的父本。显然，给定的淘汰病毒数为N。

Step 4：停止。如果算法满足停止条件，则停止搜索并返回非支配解；否则继续搜索。

4.3.2.1　编码与解码

编码是优化调度问题的首要任务，传统并行机调度问题存在两种编码方式：①扩展顺序表达方式，这是Cheng等［5］针对带有准备时间的并行机调度问题提出的一种编码方式。②分段编码方式，其原理是把每个个体长度划分为两层，第一层表示每台机器加工的工件编号，第二层表示每台机器上的加工任务总数，其染色体可描述如下：

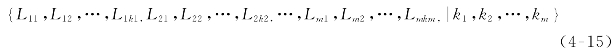
其中：Lkj表示机器k上第j次加工的工件编号；km表示在机器m上待加工工件的总数

尽管以上编码机制可以产生合法解，但是这些编码机制具有较大的随机性，将会导致解空间的冗余信息增大。此外，根据本章问题的特点，每个解需包含工件在机器上的分配信息和每个工件的加工时间信息。因此，本书采用了一种双层编码机制的解表达方式。其中，第一层代表工件在机器上的分配及排序情况，该层基于工件排序编码，遵循工件先来先加工，机器空闲就分配到该机器的原则来进行分配及排列；第二层代表工件依次从J1到Jn的实际加工时间，其染色体可描述如下：

其中：J［i］表示工件全排列的第i位置上的工件；pi表示工件Ji在相关机器上的实际加工时间。

为了解释本章采用的编码方式，假设问题的工件数n=10，机器数m=3，π=为该问题中的一个工件排序。然后根据最早完成时间（early completion time，ECT）规则［6］，构建编码与可行解之间的映射关系。该问题考虑了各工件加工时间及依赖工件序列的准备时间，如表4-2所示。

表4-2　准备时间与加工时间实例

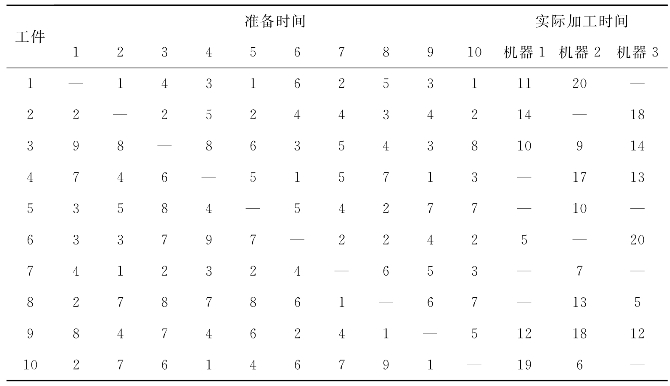
表中，符号“—”表示工件不可在对应机器上加工。为了方便解释这个编码方案，在这个实例中假设加工时间是固定的（实际情况中工件加工时间是可变化的）。对工件排 序执行最早完工时间规则，可推导出机器1上的工件总数T1=3，机器2上的工件总数T2=4，机器3上的工件总数T3=3；机器1上的工件排序，机器3上的工件排序图4-4给出了解对应的甘特图。

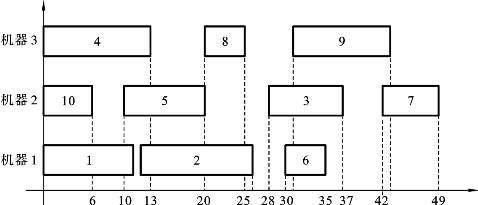
图4-4　π=［4，1，10，2，5，8，6，3，7，9］对应的甘特图（横坐标为加工时间）

4.3.2.2　种群初始化

为了提高初始种群的质量和多样性，本章采用了最早完工时间启发式方法生成一个高质量的初始个体，然后基于变换操作方式生成50%的优良种群，剩余的种群则随机产生［7］。

4.3.2.3　病毒复制

正如前所述，若病毒种群含有多个非支配水平层，则将病毒种群划分为两组：①强病毒（非支配解集）；②普通病毒（支配解集）。否则种群均处于非支配层，在这种情况下，随机将种群（非支配种群）成员划分为强病毒和普通病毒两类。不同类型病毒具有不同的搜索机制，以此实现算法的全局探索与局部寻优之间的平衡。对于强病毒成员，采用局部搜索来提高病毒成员的质量；对于普通病毒，采用全局搜索机制（如遗传算子）来加强种群的多样性。因为本章研究的问题是一个组合优化问题，所以原始的病毒复制算子不能直接应用在该问题中。本书采用的方法是，首先运用二元锦标赛选择（binary tournament selection，BTS）方法从病毒种群中选择一个病毒，若该病毒属于强病毒，则执行强病毒操作；否则执行普通病毒操作。以下分别阐述了针对强病毒与普通病毒的操作算子。

1.强病毒

对强病毒只进行微调操作，在此处只对工件的加工时间进行调整，而不改变工件的排序。强病毒生成新病毒的步骤如下。(www.daowen.com)

Step 1：首先基于工件权重的非升序排序，对每台机器上的工件进行优先级排序；然后根据工件的权重大小顺序依次扫描每台机器上的工件。

Step 2：对于每台机器，计算最大完工时间与当前机器完工时间的差值，记为spare time。如果spare time=0则执行Step 3；否则执行如下操作：按照工件权重的优先级关系，首先计算出权重最大工件的可释放时间，记为available release time。然后取spare time与available release time中的较小值作为当前工件的实际释放时间release time，即release time=min（spare time，available release time），并更新当前机器上该工件及后续工件的开始时间和完工时间。同时，重新计算当前机器对应的完工时间差，即spare time=spare time-release time。如果spare time＞0，则对权重第二大的工件执行以上操作，直到spare time≤0。否则，依次扫描机器上其他工件（基于工件权重的优先级关系的顺序扫描）并执行以上操作。

Step 3：对下一台机器执行Step 2，若机器的spare time≤0，则终止扫描；否则，直到扫描完所有机器上的工件为止。

图4-5解释了针对强病毒的这种微调操作，其中工件排序π=［4，1，10，2，5，8，6，3，7，9］。根据ECT规则，选择工件要分配的机器。机器1上的工件排序πT（1）=机器3上的工件排序πT（3）=［4，8，9］。假设工件1到工件10的权重依次为［0.2，0.3，0.1，0.5，0.4，0.6，0.5，0.9，0.1，0.1］，则根据权重大小进行排序，机器1上的工件扫描顺序为［6，2，1］。计算最大完工时间与当前机器的完工时间的差，即spare time=49-35=14，假设该机器上工件6的加工时间取值范围为［4，17］，它在机器1上的实际加工时间为5。因此，工件6的可释放时间available release time=17-5=12。然后取spare time与available release time的较小值，即实际释放时间release time=min（spare time，available release time）=12，更新当前工件的完工时间（此时的完工时间为47）、后续工件的开始时间及完工时间，同时计算当前机器的spare time=2。而机器1上的工件1和工件2的加工时间已经取其上限了，无释放时间。再扫描机器2上的工件，因为机器2的spare time=0，所以直接扫描机器3上的工件。计算机器3的spare time=6。根据扫描规则，首先扫描工件8，假设机器3上工件6的加工时间取值范围为［4，8］，实际加工时间为5，可释放时间为3，并更新当前工件及后续工件（即工件9）的开始时间和完工时间，此时机器3的spare time=3。然后扫描工件4，其可释放时间为3，并更新当前工件及后续工件的各项时间，正好此时的spare time=0，终止扫描。

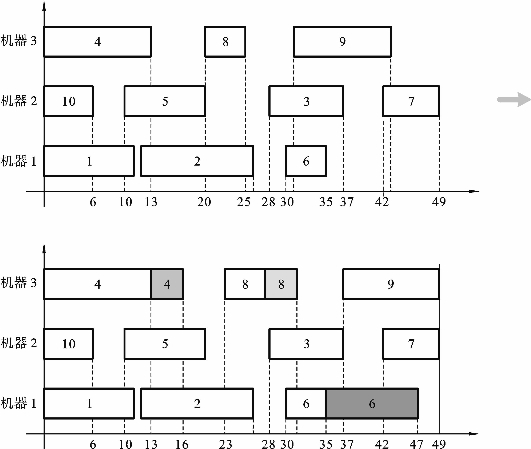
图4-5　强病毒微调操作（横坐标为加工时间）

但是这种策略会导致工件加工时间不断延长，最终使最大完工时间目标恶化。同时，随着问题规模的增大，该策略的计算时间也会呈指数增长。为了防止此类问题的出现，可在算法搜索的后期对种群实施该策略，一方面降低最大完工时间目标值，另一方面有效地缩短计算时间。本章中，搜索的后期为种群寻优的最后一次迭代。

2.普通病毒

普通病毒产生新病毒的步骤如下。

普通病毒的作用在于探索未知区域的细胞，因此它们具有较强的全局搜索能力。交叉操作主要是为了产生新子代，同时尽可能地保留基因的有效模式，以此提高算法的搜索能力。交叉操作是GA中的关键步骤，很多交叉方法在GA中已经得到较好的应用，如DEB等［4］提到的不同交叉方法。本章结合问题的特征，主要采用部分匹配交叉［8］和换位变异操作。其具体步骤如下。

1）部分匹配交叉（作用于工件序列部分）

Step 1：子串选择。随机生成两个交叉点，定义两点之间的区域为匹配区域。如图4-6所示，随机产生两个交叉点，即位置3和位置6上的点；然后定义这两点之间的区域（深色部分区域）为匹配区域。

图4-6　子串选择

Step 2：子串交换。交换两个父代的子串区域，产生临时子代，如图4-7所示。

图4-7　子串交换

Step 3：确定匹配列表。基于选择的子串，确定匹配关系。其映射关系如图4-8所示。

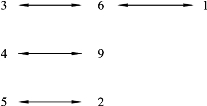
图4-8　映射关系

Step 4：子代合法化。依据匹配关系对原始子代进行合法化处理，如图4-9所示。

2）调整加工时间（作用于时间矩阵部分）

在相同工件序列情况下，具有不同加工时间矩阵的解会产生不同的最大完工时间和额外资源成本。为了保证算法搜索空间的多样性，有必要设置不同的加工时间。在这里，对时间矩阵部分的数据进行了重新调整，并保证了这些加工时间的合理性。对时间矩阵的调整规则如下：

图4-9　子代合法化

式中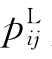：为工件i在机器j上的加工时间的下限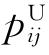；表示工件i在机器j上的加工时间的上限；pij表示工件i在机器j上的实际加工时间。

图4-10展示了这个时间矩阵调整过程，假设有4个工件在3台不相关并行机上进行分配且加工。工件1和工件4都在机器1上进行加工，对应的实际加工时间分别为4和2；工件2在机器3上进行加工且实际加工时间为8；工件3在机器2上进行加工，对应的实际加工时间为3。加工时间调整（对工件1和工件3的加工时间进行调整）之后，工件1在机器1上的实际加工时间为5，工件3在机器2上的实际加工时间为2。

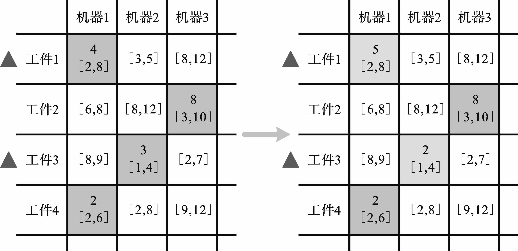
图4-10　时间矩阵调整过程