加工时间可控的并行机调度问题（parallel machine scheduling problem with controllable processing times）通常具有以下特征：

（1）每个工件的操作总数ni=1；

（2）每个工件均要在机器集M中的某一台机器上进行加工；

（3）工件加工时间可通过额外资源分配来进行控制，即工件加工时间可在一定范围内变化，但需要消耗额外的资源。

加工时间可控的并行机调度问题可分为以下三类。

（1）加工时间可控的相同并行机调度问题：有n个待加工工件的集合J在m台机器组成的集合M上进行加工，工件在任意一台机器上的加工时间区间［］是一样的，工件在加工过程中满足不可中断约束和机器唯一性约束。

（2）加工时间可控的均匀并行机调度问题：有n个待加工工件的集合J在m台机器组成的集合M上进行加工，机器Mk的加工速度为sk，工件在机器Mk上的加工时间区间为［］，工件的加工过程满足不可中断约束和机器唯一性约束。

（3）加工时间可控的不相关并行机调度问题：有n个待加工工件的集合J在m台机器组成的集合M上进行加工，工件Ji在机器Mk上的加工时间区间为工件的加工过程满足不可中断约束和机器唯一性约束。

本章研究了加工时间可控的不相关并行机调度问题，首先建立了相关问题的混合整数规划数学模型，其优化目标是同时最小化最大完工时间和额外资源消耗，该模型考虑了依赖工序的准备时间（sequence-dependent setup times，SDST）。在所研究的问题中，工件集合在不相关机器集合中进行加工，准备时间被认为是与机器和工件相关的。因此，当工件j紧接着工件i在机器k上加工时，存在准备时间Sijk。此外，该问题的相关假设如下：

①工件和机器在零时刻均可用；

②机器之间的传输时间可以忽略；

③工件在每台机器上的加工时间范围可能是不同的；

④加工开始后工件满足操作不可中断约束；

⑤每台机器能够加工某些工件；

⑥每台机器在任一时刻最多只能加工一个工件。

在构建该问题的数学模型之前，首先定义以下符号和决策变量。

1.符号

n：工件的总数。

m：可用机器的总数。

i，j，h：工件索引。(www.daowen.com)

k：机器索引。

Ji：第i个工件。

J：工件集合，

Mk：第k个机器。

M：机器集合，M=

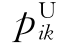：工件Ji在机器Mk上的最大加工时间。

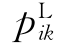：工件Ji在机器Mk上的最小加工时间。

Sijk：工件Ji和Jj在机器Mk上的准备时间。

L：一个正无穷大的数。

ui：工件Ji的单位时间压缩量所需代价的惩罚系数。

Ci：工件Ji的完工时间。

Cmax：最大完工时间。

2.决策变量

pik：工件Ji在机器Mk上的实际加工时间（连续变量）。

该问题的数学模型构建如下：

约束条件：

公式（4-1）和公式（4-2）说明了该问题的优化目标是同时最小化最大完工时间和额外资源消耗；公式（4-3）确保了虚拟工件0需优先于其他工件在机器上进行加工，随后其他工件才能依次进行加工；公式（4-4）确保了每台机器只能加工一个工件，且这台机器能够加工这个工件；公式（4-5）确保了在同一机器上加工另一个工件前最多存在一个工件；公式（4-6）保证了所有工件都必须在机器上进行加工；公式（4-7）说明了工件i只能被一台机器加工；公式（4-8）和公式（4-9）共同保证了只有前一工件完成后机器才能对当前工件进行加工，中间无闲置时间且工件满足无中断约束；公式（4-10）定义了最大完工时间；公式（4-11）给出了加工时间的约束范围。

该问题的求解目标是确定工件在机器上的分配任务及工件在每台机器上的排序，以便找到同时最小化最大完工时间和额外资源消耗的折中解。我们知道，最大完工时间指标下的经典并行机调度问题已是NP难问题，加工时间可控的并行机调度问题更是一个NP难问题。显然，传统精确算法很难在有效时间内求得该类大规模问题的最优解，而元启发式算法对求解这类组合优化问题是十分可行有效的。所以，本章设计了高效的混合算法来求解该类问题。