正如前文所述，MODGWO算法主要包含了两种改进策略：一种是新的离散编码机制，一种是成本降低策略。以下分别探讨这两种策略的有效性。

3.4.3.1　编码方式的有效性

为了验证编码方式的有效性，实验比较了随机键编码方式与本章提出的离散编码方式在部分问题（中等规模问题和大规模问题）上的结果。在本实验中，MODGWOsk表示基于随机键编码方式的MODGWO算法，有关随机键编码方法的详情可参考Nearchou［9］的文章。由于随机键编码方式在一定程度上制约了更新操作的实施，为了适应这种编码方式，MODGWOsk算法采用的更新算子为模拟二进制交叉算子（simulated binary crossover）SBX和多项式变异算子（polynominal mutation crossover），分布系数均为20，交叉和变异概率分别为0.9和0.2。此外，MODGWOsk算法也采用了成本降低策略。在实施该策略时，MODGWOsk算法需将实数编码机制转化为离散编码机制，而MODGWO算法本身就采用了离散编码机制。本节对MODGWOsk算法和MODGWO算法在20个问题上分别独立实施30次运算，并验证了离散编码机制策略的有效性。表3-3记录了30次独立运算各性能指标的平均值和标准差的统计结果。

表3-3　MODGWOsk和MODGWO获得的各性能指标的平均值和标准差

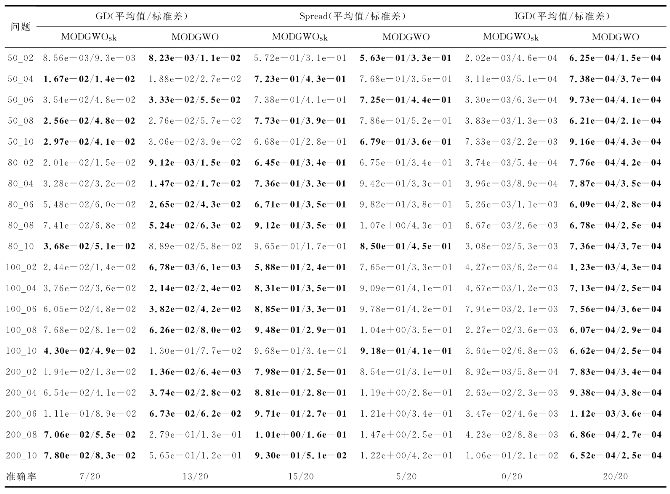
注：8.56e-03表示8.56×10-3，其余含义同。

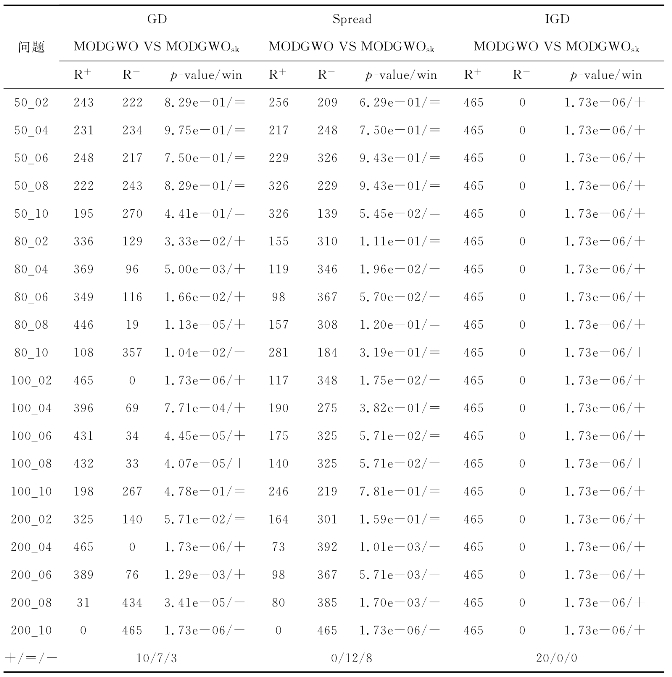
在性能指标GD、Spread和IGD上，MODGWO算法可分别在13个、5个及20个问题上获得最优结果，而MODGWOsk算法却只能在7个、15个和0个问题上取得对应最佳结果。表3-4统计出了这些结果的Wilcoxon符号秩检验的p值（p-value）。从表3-4可看出，就指标GD和IGD而言，MODGWO算法比它的竞争者具有数量更多的“+”，这说明MODGWO算法在GD和IGD指标上要显著地优于它的竞争者。在GD和IGD指标上，MODGWO算法具有优越性的原因在于其编码机制，即相比随机键编码机制，离散编码机制在搜索过程中可有效地避免信息冗余。同时，在初始化阶段，一个解的工件排序是基于交货期的非降序排列，另外一个解的加工时间为正常加工时间，即加工时间压缩量为零，从而在一定程度上确保了解的质量。但就分布性能而言，MODGWO算法在大多数问题上要显著地劣于MODGWOsk算法。其原因在于虽然随机键编码机制带来信息冗余度的增加，但它也有较大机会来搜索不同区域的解，从而具有良好的分布性能。

表3-4　各指标下的Wilcoxon符号秩检验结果（显著性水平α=0.05）

(www.daowen.com)

3.4.3.2　成本降低策略

为了验证成本降低策略的有效性，将MODGWO算法与不带该策略的MODGWO算法进行了实验对比。在本实验中，MODGWO1表示不包含成本降低策略的算法。这两种算法的参数设置与上面实验的设置相同。本实验对这两种算法在每个问题上分别独立运行了30次。表3-5记录了这两种算法在这20个问题上获得的性能指标统计结果（平均值和标准差）。表3-6给出了30次独立运算结果的Wilcoxon符号秩检验的p值。

表3-5　MODGWO1和MODGWO获得的各性能指标的平均值和标准差

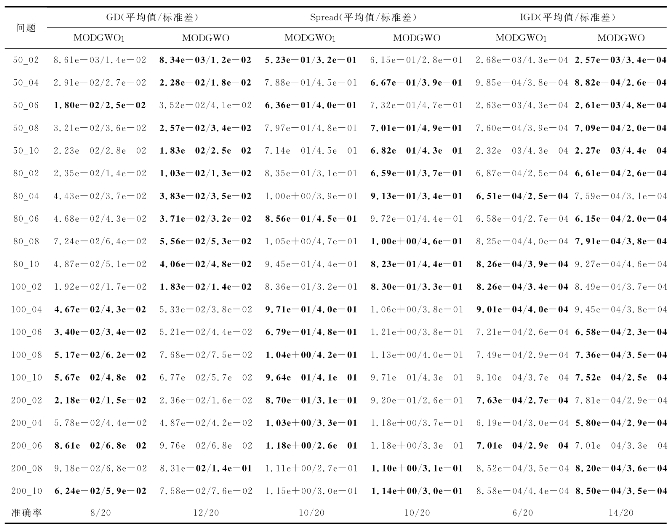
表3-6　各指标下的Wilcoxon符号秩检验结果（显著性水平α=0.05）

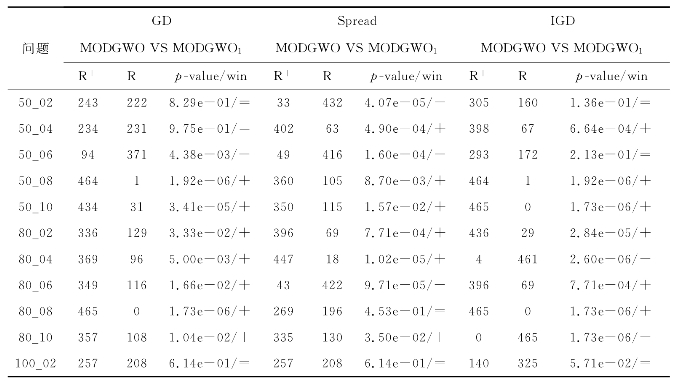
续表

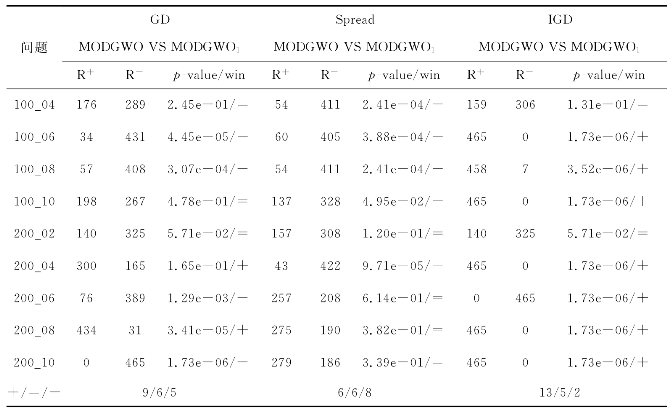
对于性能指标GD、Spread和IGD，MODGWO算法可以分别获得12个、10个及14个问题上的最优结果，而MODGWO1算法在8个、10个和6个问题上取得了最佳结果。为了进一步验证其结果的显著性，比较这些结果的p值。从表3-6可看出，对于性能指标GD和IGD，MODGWO算法比它的竞争者具有数量更多的“+”。因此，MODGWO算法在GD和IGD指标上要显著地优于MODGWO1算法，这说明采用成本降低策略的MODGWO算法具有较好的收敛性能和覆盖性能。成本降低策略具体显著优越性的根本原因在于它能够在不改变工件加工序列的情况下，减少总压缩成本且保持总延迟时间不变。通过调整工件的压缩加工时间，压缩成本可在不影响总延迟时间的情况下进一步减少，成本降低策略可在一定程度上提高算法的局部寻优能力，最终使生产系统的整体性能有所提高。