原始GWO算法主要用于求解单目标连续优化问题，而本章研究的问题是一个多目标离散优化问题，同时也是一个NP难问题。基于传统的梯度数学方法难以在可接受的计算时间内求出大规模调度问题的有效解，而元启发式算法（metaheuristics）在有限时间内可找到近似最优解，甚至最优解。因此，本章的主要工作是设计一种基于GA与GWO算法的混合多目标进化算法，记为MODGWO，来求解加工时间可控的单机调度问题（single-machine scheduling problem with controllable processing times，SSPCPT）。图3-4展示了该混合多目标进化算法MODGWO的基本流程。

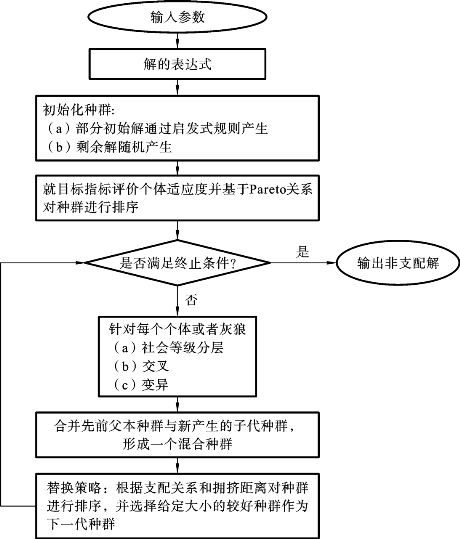
图3-4　MODGWO算法流程图

MODGWO算法的主要步骤如下。

Step 1：种群初始化。根据编码机制和种群初始化策略，产生初始狼群（种群）。基于最大完工时间和额外资源消耗指标来评价这些狼群个体，并采用快速非支配排序方法（fast non-dominated sorting method）对狼群个体进行分层排序。

Step 2：更新操作。

Step 2.1：社会等级分层。根据Pareto支配关系，种群可被划分为多个非支配水平。如果种群存在三个以上的非支配水平层，可将位于第一层非支配水平的解称为α，处于第二层非支配水平的解称为β，处于第三层非支配水平的解称为δ。

Step 2.2：位置更新操作。根据问题的特点，采用GA中的交叉、变异操作算子来更新种群。

Step 3：成本降低策略。多目标优化问题与单目标优化问题不同，在多目标优化问题中，一个目标的改善将会导致另外一个目标的恶化。因此，需要采用特殊的方法来提升整体的性能。虽然可控加工时间的引入增加了问题求解的难度，但加工时间的可控属性为获取问题的高质量解也带来了灵活性，从而为提升生产系统的整体性能提供了便利。因此，本书利用了该属性来加强探索寻优机制。因为开采寻优机制通常发生在搜索的后期，所以当函数评价次数达到一定值时，就实施该搜索机制。

Step 4：精英保留策略。种群规模为N的父本种群Pt和相同规模的子代种群Qt合并为一个大小为2N的种群Rt。然后评价该合并的种群，并根据非支配排序和拥挤距离选择出较好的前N个最佳个体作为下一代的父本。具体操作过程如图3-5所示。

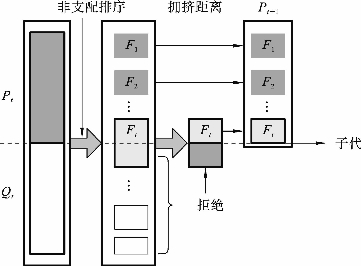
图3-5　基于非支配排序和拥挤距离的更新操作

Step 5：终止。如果算法满足停止条件，则停止搜索并返回非支配解；否则继续搜索。

3.3.2.1　编码与解码

求解调度问题的首要问题在于编码和解码。与传统调度问题中加工时间是固定的不同，SSPCPT中加工时间是可控的。它需同时处理工件排序和工件加工时间压缩量两个子任务。因此，本小节提出一种新的离散编码机制以适应问题的特征。该编码机制包含了两层信息：第一层表示工件排序，记作π；第二层表示工件加工时间压缩量，记作x。尽管Nearchou［9］针对该问题也提出了一种双层编码机制，但是他采用的编码方式实际上是一种基于随机键的编码方式，这种编码方式会导致信息的冗余。而本小节提出的编码方式可有效地避免信息冗余。

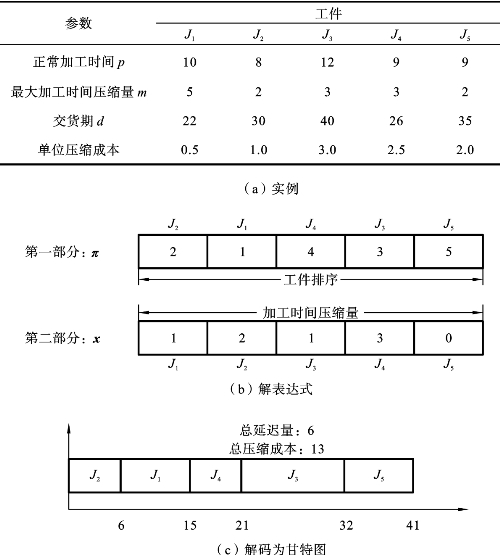
图3-6　编码与解码实例

为了详细地解释本小节提出的编码方式，图3-6给出了一个规模为5工件的单机编码与解码实例。这个解包含了两层信息：第一层是工件排序，即π=（2，1，4，3，5）；第二层是工件加工时间压缩量，即x=（1，2，1，3，0）。这两层存在着对应的映射关系，每个工件都有一个对应的加工时间压缩量。将工位π（i）位置上的工件记为Jk，它对应的加工时间压缩量为xk。例如，在排序中的第一个工位π（1）对应的是工件J2，工件J2的加工时间压缩量x2=2。同理，在序列中的第二个工位π（2）对应的是工件J1，该工件的加工时间压缩量为x1=1。因此，对于该工件排序π=（2，1，4，3，5），其对应的压缩时间向量为（2，1，3，1，0）。采用这种编码方法容易产生可行解。此外，该编码机制具有以下两个优点：

（1）编码结构简单，它包含了两层信息，即工件排序和工件加工时间压缩量。

（2）相比随机键编码方式，采用离散编码机制通常可有效地减少信息冗余。

3.3.2.2　种群初始化

正如前文所述，每个解均由一个工件排序向量和一个压缩时间向量构成。为了确保解的质量和多样性，其中一个解的工件排序是基于交货期的非降序排列。准确地说，该解具有以下特征属性：如果工件l和工件m满足pl＜pm且dl＜dm（l，m=1，2，…，n），则存在着一个最优加工排列，使工件l优先于工件m加工。种群中另一个解的加工时间为正常加工时间，即加工时间压缩量为零。剩余种群随机产生，其表达式如下：

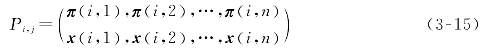
式中：π（i，n）表示第i个解上的第n个位置上的工件；x（i，n）表示第i个解上的第n个工件的加工时间压缩量。

产生初始化种群P，同时构造一个临时集合P＇。迭代搜索开始时，先将第一个个体放入集合P＇中，再依次将集合P中的个体放入构造集合P＇中。然后将当前解p依次与集合P＇中每个元素进行比较，淘汰掉P＇中被p支配的个体（解），如果P＇中任意一个个体都支配p，则从P＇中将p淘汰。构造非支配解集的伪代码如下所示。

执行以上算法时，集合P中的第二个个体只需比较一次，P中的第三个个体最多需要两次比较操作，以此类推，P中的第N个个体最多需要比较N-1次。在最坏的情况下，比较操作的总次数为N2/2。此外，考虑到每次比较时有m个目标，所以该方法的时间复杂度为O（mN2）。

3.3.2.3　社会等级分层

GWO算法的核心思想是通过当前种群中的三个最佳个体来引导其他个体向潜在的最优解方向进行搜索。但是，由于多目标优化问题中各子目标内在的相互冲突特点，其解通常不是一个解而是一个被称为非支配解的折中解集合。也就是说，对于一个折中解，一个目标性能的改善可能会导致其他目标性能的恶化。因此，结合多目标优化问题的特点，每个个体都被分配一个秩（即非支配水平）。根据Pareto支配关系，种群可以被划分为多个秩层，位于第一层秩的个体被记为α。如果存在第二、第三层秩，位于第二、第三层秩的个体分别被记为β和δ，而剩下的个体被记为ω。在本章中，最佳三个个体来自以下三个假设：

（1）如果当前种群都处在非支配层，即第一层秩上，则从种群中随机选择三个个体作为α、β和δ；

（2）如果当前种群仅有两层秩，则α来源于第一层秩内的个体，β和δ来自第二层秩中的个体；

（3）如果当前种群存在三层或三层以上的秩，则α、β、δ分别来源于第一、第二及第三层秩内的个体。

3.3.2.4　更新操作

显然，GWO算法的操作算子不能直接应用在SSPCPT上。为了克服该问题，采用传统的交叉和变异算子进行操作。交叉算子可以探索解空间的未知区域。对于解的第一层（即π），使用部分匹配交叉算子（partly mapped crossover，PMX［10］）来更新工件排序部分；对于解的第二层，采用双点交叉算子来对加工时间压缩量部分进行更新。具体的交叉步骤如下。

1）对于解的第一层（见图3-7）

Step 1：选择子串。生成两个点，并定义这两点之间的区域为匹配区域。

Step 2：交换子串。将父本上的匹配区域进行交换，以便生成临时子代。

Step 3：映射关系。确定相互矛盾元素的映射关系，也就是某个工件在序列中出现了多次的元素，定义交叉部分序列的映射关系。(www.daowen.com)

Step 4：合法化子代。通过映射关系的信息使工件序列部分合法化。

2）对于解的第二层（见图3-8）

Step 1：选择子串。随机生成两个点，并定义两点之间的区域为交叉区域。

Step 2：交换子串。交换父本上的匹配区域来产生子代。

变异算子有助于算法跳出局部最优解。在此采用两种变异算子，它们均以0.5的概率被选中进行操作。第一种变异算子是交换变异，其只能作用在工件排序部分。

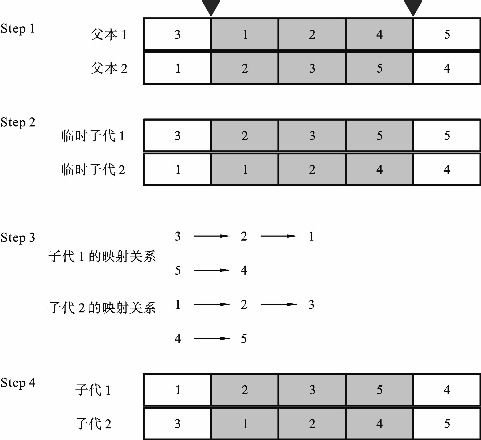
图3-7　部分匹配交叉

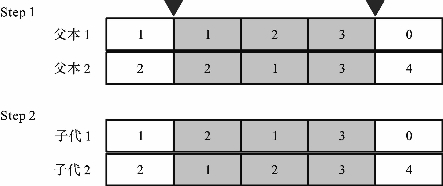
图3-8　双点交叉

第二种变异算子只能应用在解的第二层，其可调节加工时间压缩量。图3-9展示了这两种变异算子。图3-9（a）给出了第一种变异技术的操作过程，开始的工件序列π=（2，1，4，3，5）。若随机选择的两个交叉点（即第2位置和第4位置上的点），交换对应的工件1和工件3，则交换后的工件排序变为π=（2，3，4，1，5）。图3-9（b）展示了第二种变异技术的操作过程。首先随机选择两个交叉的点（如第2位置和第4位置上的点），然后随机产生可行整数来替换原始的值。例如，在工序排列的第2位置上的工件2的加工时间压缩量被替换成了一个新值1。而处于第4位置的工件4对应的加工时间压缩量更新为数值2。这些值都是在其各自范围内变化的，因此，更新后的子代仍然是可行的。

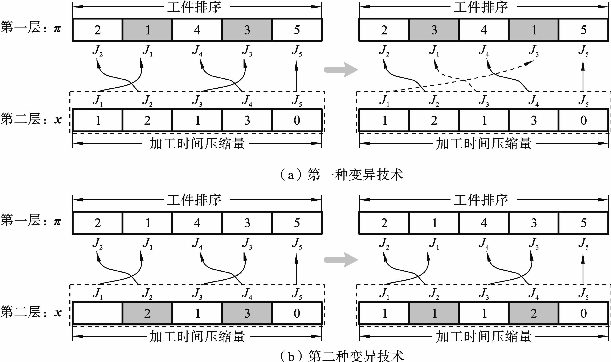
图3-9　两种变异算子

3.3.2.5　成本降低策略

通常，元启发式算法与局部搜索方法相结合可提高算法的性能［11］。在本章中，虽然没有将局部搜索策略引入改进的算法中，但是却提出了一种释放成本的策略来改善解的质量。这种策略在不改变工件加工序列的情况下，可以减少总压缩成本且保持总延迟时间不变。根据问题的特点，通过调整工件的加工时间压缩量，总压缩成本可在不影响总延迟时间的情况下进一步减少。因此，对于一个给定的工件序列，这种策略在一定程度上可以改善解的质量，而且计算复杂度为O（n）。本章提出的成本降低策略的步骤如下。

Step 1：i=n；SC=∅；SE（j）=∅，∀j=1，2，…，n（∅是空集）。SC是释放成本集合，SE（i）是紧接中工件π（i）的提前集合。

Step 2：计算Cπ（i）-dπ（i）。如果Cπ（i）-dπ（i）≥0，则执行Step 4；否则转向Step 3。

Step 3：当Cπ（i）-dπ（i）＜0时，执行下面的循环步骤直到满足Cπ（i）-dπ（i）≥0或者i＜1为止。

Step 3.1：计算工件π（i）的完工提前时间，即Eπ（i）=，并更新集合

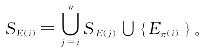
Step 3.2：获取当前集合中最小完工提前时间元素m Eπ（i）=min SE（i），并计算释放成本，然后将值Costπ（i）放入集合SC中，i=i-1。

Step 4：如果SC不是一个空集，找出集合SC中的最大元素Cost，且对应的工件记为Jπ（k）。同时更新该工件的加工时间压缩量和工件π（k）后面工件的完工时间。

为了进一步解释这个策略，以下采用了一个实例来进行说明。实例1考虑了一个5工件的单机调度问题，如表3-1所示。图3-10展示了工件工序为π=（2，3，4，1，5）且压缩时间向量为x=（4，1，1，1，0）的甘特图。该解对应的目标函数值分别是总延迟时间为2和总压缩成本为2.6。

表3-1　实例1的数据

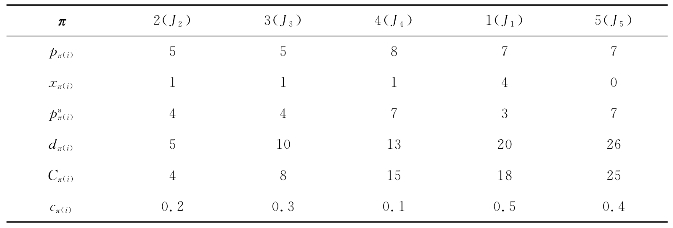
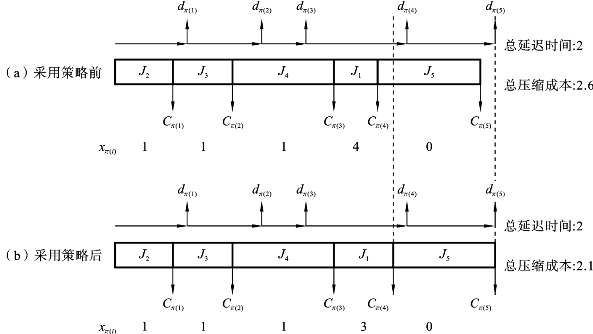
图3-10　实例1对应的甘特图

若执行以下策略，可有效降低目标函数值。

Step 1：i=5；SC=∅；SE（j）=∅，∀j=1，2，…，5。

Step 2：计算Cπ（5）-dπ（5）=25-26=-1＜0，并执行Step 3。

Step 3：执行以下操作。

Step 3.1：计算完工提前时间

Step 3.2：找出最小的工件完工提前时间m Eπ（5）=min SE（5）=1；计算该工件的释放成本将Costπ（i）添加到集合SC

Step 4：计算Cπ（4）-dπ（4）=-2＜0，并执行Step 5。

Step 5：执行以下操作。

Step 5.1：

Step 5.2：找出最小的工件完工提前时间m Eπ（4）=min SE（4）=1；计算该工件的释放成本

Step 6：计算Cπ（3）-dπ（3）=2＞0，并执行Step 7。

Step 7：从集合SC中选择成本最大的工件，也就是工件π（4）。xπ（4）=xπ（4）-对应的总延迟时间和总压缩成本分别被更新为2和2.1。注意：总延迟时间不变，但总压缩成本减少了。