本章研究的调度问题可描述为：n个独立的工件在单台机器上零时刻均可用，机器在每一时刻最多只能加工一个工件。一旦工件开始被加工，加工操作不许中断。每个工件均有一个正常的离散加工时间，工件的加工时间可通过分配额外的可用资源而被压缩，但会产生额外的压缩成本。在正常加工时间下，工件加工不会产生额外的附加成本。

为了构建加工时间可控的单机调度问题数学模型，本章所使用的符号与决策变量如下。

1.符号

n：工件总数。

j，k：工件索引号。

Jj：工件j。

J［i］：序列中第i个位置上的工件。

π：工件的加工排序，即

pj：工件j的正常加工时间。

：工件j的最小允许加工时间。

mj：工件j的最大允许压缩量

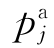：工件j的实际加工时间。(www.daowen.com)

cj：工件j的单位压缩成本。

dj：工件j的交货期。

Tj：工件j的延迟时间。

Sj：工件j的开始时间。

M：一个无穷大正数。

2.决策变量

xj：工件j的加工时间压缩量（离散变量）。

本章研究的问题是传统单机调度问题的一个扩展形式，它可被定义成一个多目标数学模型，该数学模型表示如下：

约束条件：

公式（3-1）和公式（3-2）共同定义了该问题的目标是最小化总延迟时间和总压缩成本；公式（3-3）和公式（3-4）确定了工件之间的优先级关系，并定义了一个工件在任何时刻都可被加工；公式（3-5）确保了工件序列中每一个工件延迟时间的约束条件；公式（3-6）限制了所有工件的加工时间压缩量；公式（3-7）限制了变量的非负性。相比其他类型的车间调度问题，该调度问题虽然很简单，但却是一个NP难问题［1］。因此，该问题仍然具有探索和研究的意义。