一般来说，多目标优化问题（MOP）指的是由多个目标函数构成且需满足一定约束条件的优化问题。这些目标函数之间通常是相互冲突的，所以多目标优化问题的“优化解”是对于所有目标函数而言均可接受的满意解。从数学观点来看，当优化目标函数的数目超过一个时，该类问题被称为多目标问题。与单目标优化问题（SOP）不同，多目标优化问题的优化结果通常不是一个解，而是一组被称为非支配解或折中解的解，形成解集。不失一般性，寻求最小值的多目标优化问题数学模型可定义如下：

式中：x为决策向量；f（x）为目标函数；Rn为可行解集合；n为决策向量的维度；m为目标函数的个数。

在此基础上，有关Pareto支配关系及其定义如下。

定义1（可行解集合）：对于x∈Rn，如果x满足问题的约束条件，则x就是多目标优化问题中的一个可行解。所有可行解构成的集合称为可行解集合，记为Xf。

定义2（Pareto占优）：xp和xq是两个不同的可行解，如果xp支配xq（记作xp＜xq），则须满足如下约束条件：

（1）对于所有子目标，xp不劣于xq，即

（2）至少存在一个子目标，使xp优于xq，即

其中：m表示多目标优化问题中目标函数的个数；xp是非支配的，xq是被支配的，即xp＜xq。

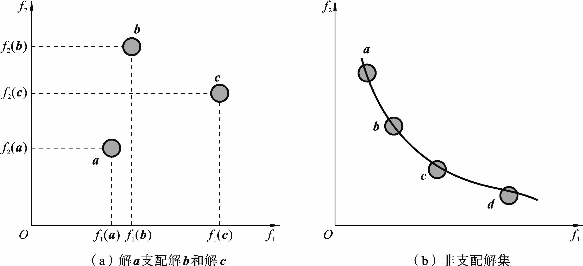
图2-1给出了多目标优化问题中可行解之间的支配关系，下面以最小化双目标函数（f1（x），f2（x））为例，对其进行解释。

(www.daowen.com)

图2-1　MOP中可行解之间的支配关系

由于这两个目标函数具有同等的重要性，因此很难确定出优良解。根据定义2，从图2-1（a）中可看出解a优于解b。因为f1（a）＜f1（b）且f2（a）＜f2（b），也就是说，在所有目标函数上解a均比解b优秀，所以解a支配解b（记作a＜b）。同理，对于解a与解c，可推导出解a支配解c（记作a＜c）。即它们满足如下条件：f1（a）＜f1（c）且f2（a）＜f2（c）。当比较解b和解c的优劣时，从图2-1（a）可知目标函数f1方向上解b优于解c（即f1（b）＜f1（c）），但在目标函数f2方向上解c优于解b（即f2（c）＜f2（b））。也就是说，解b不能支配解c，解c也不能支配解b。在该种情形下，解b与解c是相互非支配的。图2-1（b）中的解均是相互非支配的。

定义3（Pareto最优解）：当且仅当满足

条件时，解x*∈Xf是问题的一个Pareto最优解。准确地说，在可行解集合Xf中，如果不存在任何一个可行解x支配解x*，则解x*称为Pareto最优解。

定义4（Pareto最优解集）：针对一个多目标优化问题，Pareto最优解集S*可定义如下：

定义5（Pareto前端）：Pareto最优解集S*映射在目标空间的集合称为Pareto前端（Pareto front），用PF*表示：

图2-2展示了Pareto最优解集S*与其对应Pareto前端PF*的关系。

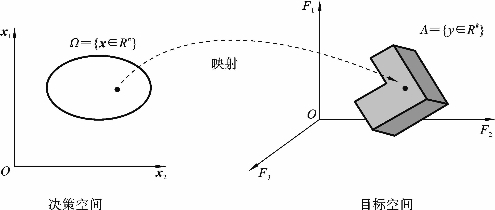
图2-2　Pareto最优解集与Pareto前端关系示意图