1.单机调度问题

单机调度（single machine scheduling，SMS）是指所有的操作任务都在一台机器上完成，需要对任务进行优化排序，通常希望找到一个可行的排序，使得某个给定的目标函数达到最小（大）值。这里的“可行”一般指在同一时刻，一台机器至多加工一个工件，一个工件也只在一台机器上加工，并且该排序满足问题特定的约束要求。

在生产调度研究领域，单机调度问题一直是研究热点。基本问题可以描述为n项相互独立的任务需要在系统中的一台机器上按顺序处理，每项任务都有加工时间、交货期等参数；此外，还须满足一些调度环境和约束条件的要求，调度目标就是要找到一个最优的任务序列使得系统总成本最低。在理论上，单机调度问题可看作其他调度问题的特殊形式。因此，深入研究单机调度问题可以更好地理解复杂的多机调度问题的结构。同时，求解单机调度问题的启发式算法也可以作为求解复杂调度问题的算法的基础。在生产实践中，复杂调度问题往往可以分解为多个单机调度问题。另外，若一条生产线上的某台机器成为瓶颈，则整条生产线的调度都要围绕该机器进行。

生产中单机调度的例子不少。比如生产线上的一台机器人负责将半成品从缓冲区搬运至机床进行加工，这就存在如何合理调度机器人的行进路径，以及安排物料搬运次序，使得机床利用率最高，且不影响后续工序生产的问题。再比如钢铁热轧车间一般会配备一座环形加热炉，切割后的各种坯料将按一定次序被放入加热炉中加热，再依次被取出进行轧制，由于坯料的加热时间都很长且不同坯料的加热时间不尽相同，因此合理安排坯料加热次序对后续工序的意义重大。

单机调度问题看似简单，然而根据排列组合的知识可知，系统中n个工件加工次序的全排列为n！。当n=20时，n！=2.4×1018，若要对所有可能排序计算出结果进行比较，即使是每秒运算109次，也要77年才能完成。显然，当n较大时单机调度问题是NP难问题，这个结论已经得到了充分论证。

2.并行机调度问题

并行机调度无论从理论还是从实际来说，在生产调度中都是十分重要的。从理论来说，它是对一道工序（一个阶段）和特殊形态下柔性（混合）流水车间的推广；从实际来讲，它重要是因为在真实世界中资源并行利用的情况是很常见的，并且并行机技术经常被用于多阶段系统的分解处理过程。

并行机调度有多种分类标准，具体分类如下。

（1）按并行机类型可分为：同速并行机（identical parallel machines）调度、非同速并行机（non-identical parallel machines）调度以及不相关并行机（unrelated parallel machines）调度。

（2）按并行机调度目标函数可分为：最小化最大完工时间、最小化拖期任务数、最小化加权绝对偏差以及最小化提前/拖期惩罚等并行机调度。

（3）按确定性可分为：确定性并行机模型和随机并行机模型。

（4）按是否可中断可分为：可中断的并行机调度和不可中断的并行机调度。中断对一台机器起到很大作用，在一台机器中，中断通常只作用于工件在不同时间点提交的情况。相反地，在并行机中，即使所有工件在同一时间提交，中断也是十分重要的。

并行机调度问题是实际生产过程中的一类典型调度问题，它研究n个工件在m台机器上的加工过程，每个工件仅需在某台机器上加工一次（假设所有机器的加工性能相同），要求某个调度序列的目标函数值最优。通常可以将并行机调度问题分为两个子问题：首先，决定所有工件在各机器上的分配问题；其次，要决定各机器上工件的加工顺序。这是并行机调度的两个本质问题。

3.流水车间调度问题

流水车间调度问题是生产调度问题中最为典型，也是最为重要的一个分支。它作为很多实际流水线生产的简化模型，具有非常广阔的应用范围，与实际工业联系最为紧密。同时，它也是目前研究最为广泛的一种调度问题。流水车间调度问题一般可以描述为n个工件J=｛1，2，…，n｝需要在m台机器M=｛1，2，…，m｝上加工，每个工件都包含m道工序，即必须依次通过机器1、机器2直到机器m才能完成加工任务。每一个工件的加工顺序相同。工件i（i=1，2，…，n）在机器j（j=1，2，…，m）上的加工时间为pi，j。在任意时刻，每一台机器最多加工一个工件，每一个工件最多只被一台机器加工。工件的运输时间、加工准备时间都包含在工件加工时间内。在流水车间调度问题中，如果每一台机器上的工件加工顺序也相同，则此问题变为置换流水车间调度问题。目标函数为最小化最大完工时间的包含m台机器的置换流水车间调度问题可记为Fm|prmu|Cmax。(www.daowen.com)

4.作业车间调度问题

作业车间调度问题，简称JSP（job-shop scheduling problem），是典型的NP难问题，也是研究车间调度问题的基础。它的研究不仅具有重要的现实意义，而且具有深远的理论意义。

JSP就是为了加工多个不同的工件而决定如何分配作为共同资源的机器，并使某个指标或多个指标最优的问题。其对机器和工件有如下约束：

（1）在不同工件的供需之间无优先级的约束；

（2）不允许某道工序在加工时被中断且每台机器不能同时处理两道及以上的工序；

（3）一个工件不能同时在两台机器上进行加工。

一般认为，这种问题属于NP难问题，并且被认为是最难解决的问题之一。以往，JSP的求解方法主要是分支定界法（branch and bound method），但其只能求解规模很小的问题，对大规模问题则无能为力。近来，对这一具有复杂解空间的问题有了一些比较好的求解方法，如遗传算法等。蚁群优化算法虽然也有应用于JSP的求解，但效果并不是很好，主要问题在于该算法容易陷入局部最优解，而且对于大规模JSP的求解，该算法的计算和收敛速度比较慢。JSP通常包括下列元素：工序的集合O=｛o1，o2，…，on｝∪｛ostart，olast｝，其中ostart和olast是两道伪工序，分别代表开始和结束。这些工序又可以根据其隶属的工件或任务，分为子集J1，J2，…，Jr。可以定义：对于o∈O，如果j（o）=i，那么o∈Ji。

对于o∈Ji，根据JSP的特点，Ji中o是完全有序的，即如果oi排在ok之前，那么oi必须在ok之前完工，记作oiok。还可以定义，在oi之前加工的工序为pred（oi），紧跟在oi之后加工的工序为succ（oi）。

O还可以根据对应的机器分成子集，即M1，M2，…，Mm。同样可以定义m（o）=i，如果o∈M，这里每道工序的加工时间为pt（o），如果用t（o）表示工序o开始加工的时间，那么JSP的数学模型可以表示如下：

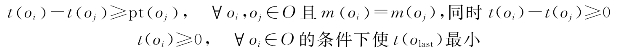
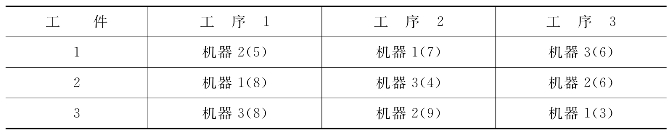
表1-1所示为一个包含3个工件，需要在3台机器上加工的JSP实例，表中括号内的数字表示在此机器上的加工时间。注意，在本书中，若无特别说明，加工时间均采用单位时间表示。

表1-1　JSP实例