风险估计又称为风险估算，是在风险识别之后，通过定量分析的方法测算风险事件发生的可能性及其对项目的影响程度的一项工作。

1．风险概率估计

（1）客观概率估计。

客观概率即根据历史统计数据或大量试验计算的实际发生概率。应用客观概率对项目风险进行的估计称为客观概率估计（客观估计），这种方法的最大缺点是需要足够的信息，通常很难满足。当项目相关历史数据比较充足时，就可以利用统计方法计算风险概率。

例如，某风险因素有 Q1，Q2， … ，Qm等m 个状态，对应的出现次数分别是 n1，n2， … ，nm，则第i 种状态出现的概率是

式中n = n1+ n2+ n3+ …+nm。

（2）主观概率估计。

主观概率是基于专家个人经验、预感或直觉而估算出来的概率。主观概率估计一般在有效统计数据不足或不可能进行试验时采用。

2．风险概率分布

概率分布是指随机变量可能出现的概率取值的分布情况。对于连续型随机变量，通常可以用概率分布函数来表示，而离散型随机变量的概率分布通常是根据个人主观判断，所得到的各种确定的概率值。在项目评估中进行概率分析时，一般只分析和研究离散型随机变量的概率分布情况。

一般情况下，概率分布函数应根据历史资料进行确定。当项目管理人员没有足够的历史资料来确定不确定因素的概率分布函数时，可以利用理论概率分布进行风险估计，也可以用概率树、蒙特卡罗模拟及CIM 模型等分析方法确定不确定因素的概率分布函数。

（1）离散型概率分布。离散型随机变量（离散型变量）是指可能值有限的输入变量，变量取各可能值的概率之和等于1。

（2）连续型概率分布。当输入变量的取值充满一个区间，无法按一定次序一一列举出来时，称为连续型随机变量。常用的连续型概率分布有正态分布、三角型分布、β 分布、经验分布。

3．概率树分析

概率树分析是通过构造概率树来估计项目风险的一种方法。从理论上讲，概率树分析适用于所有状态数有限的离散型变量，根据每个变量的状态组合计算项目评价指标。

假设变量（风险因素）有　A，B，…，M；每个变量有若干种状态 A1，A2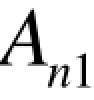，… ， ，B1，B2，… ，Bn2,…，M1，M2，… ，Mnm，各种状态发生的概率为 P ( Ai)，P ( Bi)，… ，P ( Mi)。即有

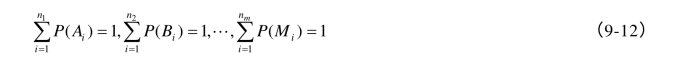
所有变量的各种状态的组合共有 n1× n2× …×nm种，相应组合的联合概率为 P ( Ai)×P ( Bi)× …×P ( Mi)。

概率树分析就是用树形图来表示各种各个变量的各种状态组合，分别计算在每种状态组合下的评价指标及相应的概率，得到评价指标的概率分布。然后统计出评价指标低于或高于基准值的累计概率，并绘制累计概率曲线，计算评价指标的期望值、方差、标准差和离散系数等。

采用概率树分析，各个变量之间必须相互独立，否则联合概率就不是简单的各种状态概率之积。此外，由于计算量随变量或状态的增长呈几何级增长，所以在实际运用中一般将变量数限制在3 个及其以下，状态数也不宜超过3 个，这样组合状态可控制在27 个之内。

4．蒙特卡洛模拟

当在项目评价中输入的随机变量个数多于三个，每个输入变量可能出现三种以上状态时，上述方法就会非常烦琐，必须采用其他风险分析方法，蒙特卡洛模拟技术就是其中之一。

蒙特卡洛模拟技术的原理是用随机抽样的方法抽取一组输入变量的数值，计算项目评价指标，重复这个方法足够多以后即可获得评价指标的概率分布及累计概率分布等数据，据此计算项目由可行转变为不可行的概率，从而估计项目投资所承担的风险。

（1）蒙特卡洛模拟的步骤有：

①确定风险分析所采用的评价指标，如净现值、内部收益率等；

②确定影响项目评价指标的主要风险因素，如建设投资、销售价格、经营成本等；

③估计主要风险因素的概率分布，并用数学模型表示；

④为各风险因素独立抽取随机数；

⑤将抽得的各随机数转化为各风险因素的抽样值；

⑥将抽样值组成一组项目评价基础数据，并据此计算相应的评价指标；

⑦重复④～⑥步骤，直至达到预定的模拟次数；

⑧ 整理模拟结果，计算评价指标的期望值、方差、标准差、离散系数，以及累计概率等，并可绘制累计概率图。

（2）应用蒙特卡洛模拟时应注意的问题如下。(www.daowen.com)

① 在蒙特卡洛模拟中，假设输入变量之间是相互独立的，在风险分析中会遇到输入变量的分解程度问题。变量分解得越细，输入变量个数就越多，模拟结果的可靠性就越高，但计算过程越烦琐。

如果输入变量是相关的，模拟中视为独立的进行抽样，就可能导致错误的结论。可以通过限制输入变量的分解程度或限制不确定变量个数处理，也可以进一步搜集有关信息，确定变量之间的相关性，建立函数关系。

② 蒙特卡洛模拟的模拟次数。从理论上讲，模拟次数越多越正确，从实际出发，一般应在200～500 次为宜。由于计算量巨大，蒙特卡洛模拟需要借助计算机来完成。

【例9-7】 某项目的建设投资为1 800万元，投资当年即可获得正常收益。项目年净收益呈正态分布，其期望值为300 万元，标准差为50 万元；寿命期估计为12 年到16 年，呈均匀分布。设项目基准折现率为12%，期末残值为零，试用蒙特卡洛模拟分析该项目净现值小于零的概率。

解：求解过程如下：

（1）确定评价指标。根据题意，评价指标取项目的净现值。

（2）确定主要风险因素。根据题意，项目的年净收益和寿命期为两个主要风险因素，即本例需模拟的随机变量。

（3）生成年净收益和寿命期的抽样值。

在蒙特卡洛模拟中，随机变量的变化是通过随机数来模拟的，即由随机数发生器产生随机数，然后根据随机变量的概率分布将随机数转换为相应的随机变量取值。随机数通常在[0.000，0.999）范围内抽取。

本例中年净收益服从正态分布，可先从计算器中读出一个随机数0.524，将其作为年净收益取值所对应的累计概率的一个随机值，由标准正态分布表可查得累计概率0.524　所对应的　Z　值为0.060。由公式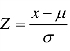可求得

即抽取的年净收益的第一个随机样本数据为303.00 万元。

本例的寿命期为均匀分布，即发生在12 年、13 年、14 年、15 年、16 年的概率均等，均为1/5＝0.20，其累计概率分布如表9-4 所示。

表9-4　累计概率分布表

然后从计算器中读取一个随机数0.291，作为寿命期取值所对应的累计概率的一个随机值。由表9-4 可知。随机数0.291 对应的寿命期为13年。这是抽取的第一个寿命期随机样本数据。

（4）计算净现值。

根据上述第一组随机样本数据（年净收益303.00万元，寿命期13年）可计算得到相应的净现值为

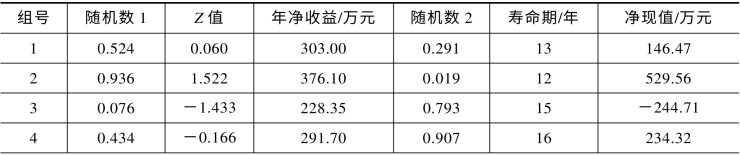
重复上述过程，可以得到方案年净收益和寿命期的其他随机样本数据及相应的净现值计算结果。一般来说，模拟分析的随机样本数据应达到200～500 组。这里，取25 组作示例，见表9-5。

表9-5　净现值计算表

续表

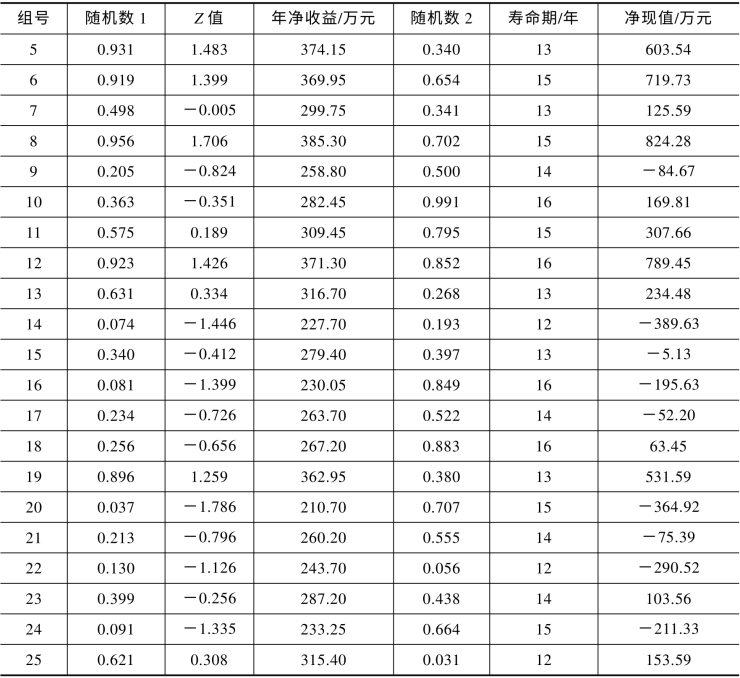
（5）计算净现值的期望值以及小于零的概率。

将表9-5 中的净现值按从小到大的顺序排列，并求和（如表9-6 所示）。由于每组净现值的概率均为1/抽样组数＝0.04，所以净现值的期望值＝3 622.95 万元（净现值之和）×0.04（概率）＝144.92 万元。表9-6 中还可以计算净现值的累计概率。由计算结果可知，项目净现值小于零的概率为0.40＋(0.44－0.40)×5.13/(63.45＋5.13)＝0.403 0，即项目不可行的概率为40.30%。

（6）计算净现值的方差、标准差和离散系数

由表9-6 中的数据可得，项目净现值的方差σ 2=122 386.94，标准差σ =349.84。离散系数为

从项目净现值小于零的概率和离散系数看，该项目的风险很大。当然，由于抽样的样本数不是足够的大，样本的代表性较差，所以上述结论可能受样本的影响较大。

表9-6　累计概率及方差计算表

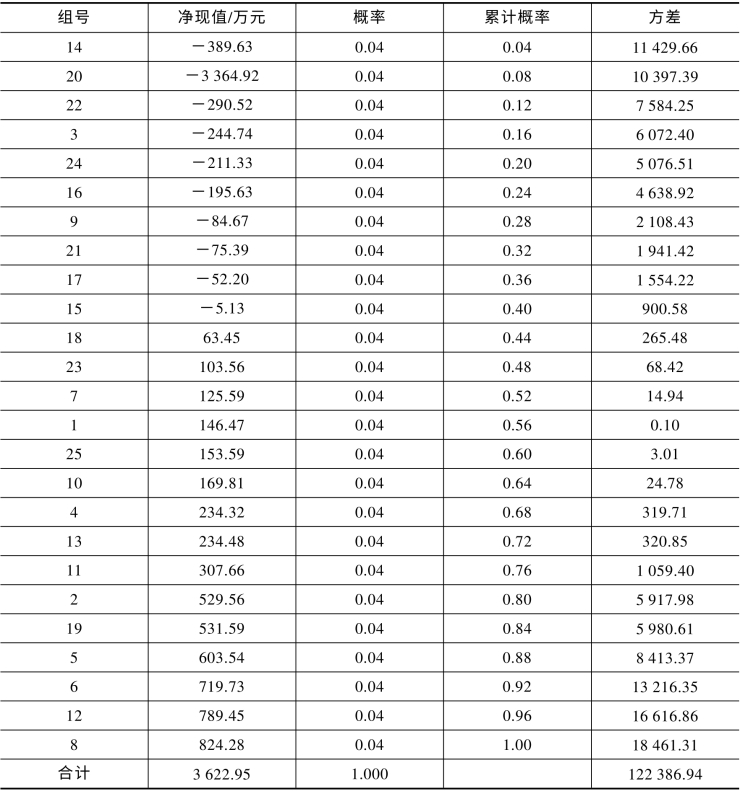
在本例中，作为不确定因素的年净收益服从正态分布，寿命期服从均匀分布。事实上，蒙特卡洛模拟可以运用于具有更多个不确定因素的情况，也适用于不确定因素的其他概率分布类型，包括无法用解析模型加以描述的经验分布。