在进行单因素敏感性分析时，当计算某特定因素变动对经济效果评价指标的影响时，假定其他因素保持不变。实际上，不确定因素往往是同时变化的，所以有必要进行多因素敏感性分析。

多因素敏感性分析要考虑被分析的各不确定因素可能的不同变动幅度的多种组合，因此，多因素敏感性分析计算起来比单因素敏感性分析要复杂得多。如果需要分析的不确定因素不超过三个，而且经济效果评价指标的计算比较简单，可以用解析法与作图法相结合的方法进行分析。进行多因素敏感性分析的假定条件是：同时变动的因素互相独立。

1．双因素敏感性分析

一次改变一个因素的敏感性分析可以得到一条曲线——敏感性曲线。但当分析两个因素同时变化的敏感性时，可以得到一个敏感面。每次同时变动两个不确定性因素的敏感性分析，叫作双因素敏感性分析。

【例9-5】 某企业一项投资方案，提供了下面的参数估计，其数据资料如表9-3 所示。假定最关键的不确定因素是初始投资和年收入，试对净年值指标进行双因素敏感性分析。

表9-3　例9-5 的方案现金流量表　单位：元

解：设X 表示初始投资变化的百分数，Y 表示年收入变化的百分数，则有

经过整理得

取NAV 的临界值，即NAV = 0，则有

例9-5 的双因素敏感性分析见图9-6。

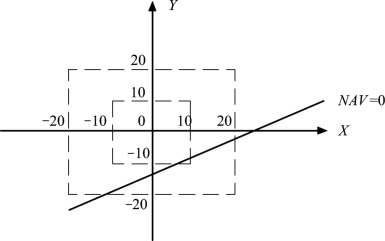
图9-6　双因素敏感性分析图

在图9-6　中，X　与　Y　的任一组合均代表初始投资和年收入变化的一个可能状态。直线Y =-0.127 3 +0.500 9X是一条临界线，在临界线上NAV= 0。在此临界线左上方的区域NAV ﹥ 0；在此临界线右下方的区域NAV﹤ 0。当初始投资和年收入同时变动时，若变动量所对应的点落到的NAV ﹤ 0区域，方案就会变为不可行。(www.daowen.com)

2．三因素敏感性分析

每次同时变动三个不确定性因素的敏感性分析，叫作三因素敏感性分析。

【例9-6】 假设上例中寿命也是一个重要的不确定因素，试对净年值指标进行初始投资、年收入和寿命进行三个因素同时变化的敏感性分析。

解：要推导出一个三维的敏感性分析数学表达式是困难的，但可通过根据每一可能的寿命画出来的一组盈亏线来考察经济效益评价指标。

如果三个因素同时变化，仍然设X 表示初始投资变化的百分数，Y 表示年收入变化的百分数，L 表示产品寿命。分析其对净年值（NAV）影响的公式为

取不同的寿命周期代入上式，则获得如下的结果，即当L＝2、3、4、5、6、7 时，有

当L= 2时，Y≥0.369 3 +1.121 5X

当L= 3时，Y≥0.092 8 +0.776 1X

当L= 4时，Y≥-0.044 9 +0.603 8X

当L= 5时，Y≥-0.123 7 +0.500 9X

当L= 6时，Y≥-0.181 9 +0.432 6X

当L= 7时，Y≥-0.224 2 +0.384 2X

根据以上方程可画出如图9-7 所示的一组盈亏线。

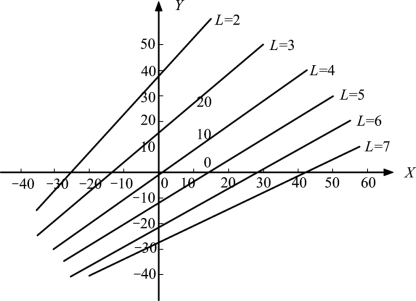
图9-7　三因素的敏感性分析图

由图9-7 可以看出，在初始投资（X）和年收入（Y）偏离最可能值±20%的变化范围内，当L＝4、5、6、7 时，均显示出良好的投资盈利效果。