资金时间价值原理和资金等值计算公式广泛应用于财务管理、投资决策、资产评估等领域。前面介绍的复利计算公式，可以按一定的利率在不同时刻作等值变换，可以将一笔等值资金变换到任何时刻，也可以等值变换为任何一种支付形式。实际进行资金等值计算时，计息期与支付期可能是相同的，但也可能出现计息期比支付期短，或计息期比支付周期长的情况，也有可能出现多种情况的混合，这样就必须针对不同的情况具体分析和计算。

1．计息期为一年的等值计算

当计息期为一年时，实际利率与名义利率相同。此时，不需要考虑利率的换算问题，直接利用年利率计算即可。

【例3-15】 某企业准备进行一项关于技术改造的投资项目，该项目预计在今后5 年中，每年年末的净现金流入分别为200、250、270、240、220 万元，如果按贴现率15%计算，本项目的现值和第5 年末的终值各是多少？

解：本题是多次支付形式的，但不是等额的，所以把每一次支付都当成是一次支付类型来处理。于是有

即本项目的现值为787.11 万元，第5 年末的未来值是1 583.26 万元。

【例3-16】 某债券是一年前发行的，面额为500 元，年限5 年，年利率10%，每年支付利息，到期还本，若投资者要求在余下的4 年中的年收益率为8%，问该债券现在的价格低于多少，投资者才会买？

解：每年支付利息为500×10%＝50（元），则有该债券在4 年内的收益情况如图3-19所示。

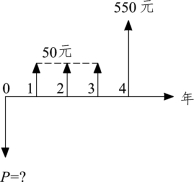
图3-19　现金流量图

所以，若投资者要求的年收益率为8%，则该债券低于533 元投资者才会买。

除了上述的应用外，计息期为一年的等值计算还有一些特殊的情况，现介绍如下。

（1）延期年金的等值计算。

【例3-17】 设年利率为10%，现存入多少钱才能正好从第四年到第八年的每年年末等额提取2 万元。

解：根据题意可得

即现存入5.7 万元，正好能从第四年到第八年的每年年末等额提取2 万元。

（2）永续年金的等值计算。

【例3-18】 某地方政府一次性投入5 000 万元建一条地方公路，年维护费为150万元，折现率为10%，求现值。

解：该公路可按无限寿命考虑，年维护费为等额年金，可利用等额支付现值公式求当n →∞时的极限来解决。

即

所以，该条公路的投资现值为6 500 万元。

（3）求解未知的利率i。

【例3-19】 某厂用67 100 元添置一台设备，每年可节约生产成本10 000 元，若这台设备可用10 年，不计残值，这笔投资将会获得多大的投资收益率？

解：根据题意，画现金流量图，如图3-20 所示。这里已知现值和等额年金，由P =A( P / A, i ,n)可以求出

查复利系数表可知，当n=10 时，i=8%，即投资收益率可达8%。

图3-20　现金流量图

（4）求解未知期数n。

【例3-20】 某企业贷款200 万元建设一个投资项目，贷款年利率为10%，第3 年投产，投产后每年收益40 万元，问投产后多少年还清本息（还清本息前，每年全部收益都用来偿还贷款）？

解：绘制现金流量图，如图3-21 所示。

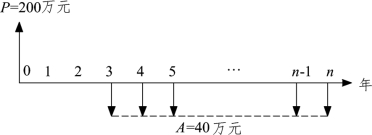
图3-21　现金流量图

由图3-21 可以看出，从第3 年、4 年到第n 年的现金流量为等额支付类型，可将此支付序列的现值计算出来，因为全部收益用来偿还贷款，所以贷款投资额应该等于全部收益的现值。即

解：

又由P ′=A( P / A, i, n)，可得(www.daowen.com)

查复利系数表可知，i=10%时，

利用插值法计算n，可得

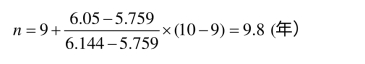
即投产后9.8 年可还清贷款的本息。

2．计息期短于1 年的等值计算

此时需考虑利率的变化，经过适当变换后，仍可利用前述公式进行计算。可分为以下3种情况。

（1）计息期与支付期相同。

当计息期与支付期相同时，首先要通过名义利率求出计息期的实际利率，确定计算期内的支付次数，然后套用资金时间价值的计算公式进行计算。

【例3-21】 年利率为12%，每半年计息1 次，从现在起连续3 年每半年等额存款200元，问与其等值的第0 年的现值是多少？

解：计息期为半年的实际利率为 i=12%/2 =6%，计息期数为n= 2 × 3 = 6 (次 )，则有

【例3-22】 某家庭欲购买一套建筑面积为80 平方米的经济适用住房，单价为3 500 元每平方米，首付款为房价的25%，其余申请公积金和商业组合抵押贷款。已知公积金和商业贷款的利率分别为4.2%和6.6%，期限均为15 年，公积金贷款的最高限额为10 万元。问该家庭申请组合抵押贷款后的最低月还款额是多少？

解：首先计算该房产的总价值，即需要贷款的总额；因为是按月还贷，所以要根据名义利率换算出贷款的实际利率，最后再计算每月还款额。即有

因此，组合贷款的月最低还款额为

（2）计息期短于支付期。

当计息期短于支付期时，如计息周期是年、季、月或周，而支付周期是年时，则属于计息周期小于支付周期。下面通过例题，说明其等值计算方法。

【例3-23】 年利率为10%，每半年计息1 次，从现在起连续3 年的等额年末支付为500元，求与其等值的第0 年的现值是多少？

解：计算方法有以下三种。

（1）先求出支付期的实际年利率，支付期为1 年，则实际年利率为

（2）可把等额支付的每一个支付看作是一次支付，利用一次支付现值公式计算。每半年计息一次，所以半年期的利率为5%，一年之中计息两次。则

（3）取一个循环周期，使这个周期的年末支付变成等值的计息期末的等额支付系列，从而使用等额支付序列计算公式计算。在年末存款500 元的等效方式是在每半年末存入一笔资金A。即

三种方法计算的结果是一致的，其等额现值都是1 237.97 万元。

通过此案例可以看出，资金的等值计算是非常灵活的。不管采用何种方法，其关键在于公式中所用利率的利率周期一定要与资金的支付周期相匹配。

（3）计息期长于支付期。

有时，会遇到支付期短于计息期的情况。在工程经济学分析中，一般是将计息期内发生的现金流量进行合并，使其与计息期的时间长度相等。按照惯例，存款必须存满整个计息期时才计算利息，而借款或贷款没有满一个计息期也计算利息。也就是说，在计息期间存入的款项在该计息期不计算利息，要到下一个计息期才计算利息；在计息期间的借款或贷款，在该计息期计算利息。按照此原则对现金流量图进行合并整理则有，相对于投资方来说，计息期的存款放在期末，计算期的取款、借款或贷款放在期初，计算期分界点处的支付保持不变。因此，在对现金流量进行合并时，计息期间的存款应放在期末，而在计息期间的应放在期初。

【例3-24】 一项财务活动的现金流量如图3-22 所示，假设年利率为8%。求其按季度计息计算的终值（即年末存款余额）。

解：通过对图3-22 中现金流量的分析可知，恰好是支付期短于计息期的情况。首先按照上述原则对此项财务活动的现金流量进行合并整理，其现金流量图如图3-23 所示。

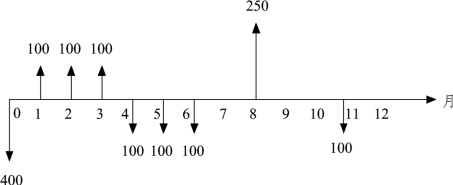
图3-22　实际现金流量图

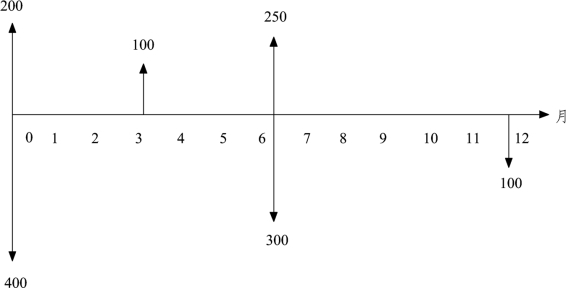
图3-23　合并整理后的现金流量图

若按季度计息，则每季度的利率为8%/4 =2%，根据合并整理后的现金流量图可计算出年末的终值为

即该项财务活动的年末存款余额为262.3 元。