在长期中，所有生产要素均可改变，长期生产函数的分析与消费者行为的分析有许多类似之处。

一方面，正如消费者可以通过购买不同的商品组合达到一定的满足程度一样，企业也可以改变要素组合来生产一定的产量。比方说，企业既可以选择高度自动化的机器设备加上少量的工人这种组合方式，也可以选择少量的机器设备和大量的工人这种组合。那么在新成立的企业中，企业应该雇用多少工人，采用多少台机器呢？企业想要扩大产量的时候，应该多雇用工人，还是应该多安装一些机器设备呢？长期生产函数的分析就要解决这一问题。

另一方面，消费者行为理论认为，虽然消费者总是希望消费更多的各类产品以实现更高的满足程度，但是最终的消费选择必须受到收入的制约；类似的，企业总是希望能生产更多的产出，但是企业的生产决策要受到来自成本的制约。因此，与消费者行为理论中引入的无差异曲线以及预算约束线类似，在长期生产函数的讨论中也有等产量线和等成本线。

两种可变生产要素的长期生产函数可以写为：

Q=f（L，K）

其中，Q 代表产量，L、K 分别代表两种可变生产要素劳动、资本的投入量。

5.4.1 等产量线

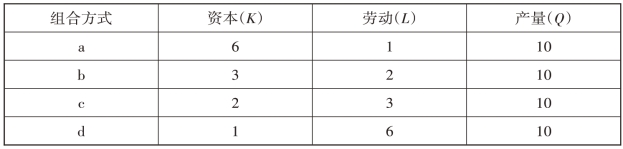
等产量曲线是表示其他条件不变时，为了得到相同的产量所需投入的两种生产要素（K 和L）的所有可能的组合所形成的一条曲线。等产量曲线类似于无差异曲线，不过它表示的不是消费者获得相同的效用，而是生产者得到相同的产量。如表5-2所示，为了得到相同的产量（Q=10），企业可以选择K和L的四种不同组合方式。根据这些信息，可做出如图5-2所示的等产量线。

表5-2 等产量表：要素组合方式及其产出

比较这种分析与无差异曲线分析的异同？

等产量线与无差异曲线的分析方法是相似的；但无差异曲线无法衡量具体的效用，等产量线却有对产量具体衡量。注意这一点有利于对消费者行为和生产者行为的理解。

在图5-2 中，横轴L 代表劳动量，纵轴K 代表资本量，Q 为等产量曲线；即曲线上任何一点所表示的资本与劳动不同数量的组合，都能生产出相同的产量。

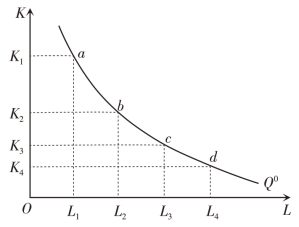
图5-2 等产量曲线

与无差异曲线相似，等产量曲线也具有一系列特征：

第一，等产量曲线总是向右下方倾斜，其斜率为负。这表明：两种生产要素在生产中具有一定的替代性；在生产者的总投入与生产要素价格既定的条件下，为了达到相同的产量，在增加一种生产要素的投入量时，必须减少另一种生产要素的投入量。

第二，等产量曲线总是凸向原点，两种生产要素的边际技术替代率的绝对值是递减的。边际技术替代率MRTS是在维持产量水平不变的条件下，增加一种生产要素的投入量与减少另一种生产要素的投入量之比。以ΔL 和ΔK 分别代表劳动和资本的变动量，MRTSLK代表以劳动代替资本的边际技术替代率，则有：

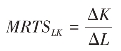
上式中，当ΔL →0时，则边际技术替代率的公式为：

可见，等产量曲线上某一点的边际技术替代率就是等产量曲线在该点斜率的绝对值。边际技术替代率应该是负值，因为一种生产要素增加，另一种生产要素就要减少。但为了方便起见，一般用其绝对值。

如图5-2，在等产量曲线Q上从a点到b点，总产量保持不变，则：

MPK×ΔK+MPL×ΔL=0

所以有：

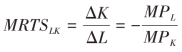
即：两种生产要素的边际技术替代率等于它们的边际产量之比的绝对值。

在两种生产要素相互替代的过程中，普遍地存在着边际技术替代率递减规律。在维持产量不变的条件下，当一种生产要素的投入量不断增加时，它每一单位能够替代的另一种生产要素的数量是递减的。

以劳动对资本的替代为例，随着劳动对资本的不断替代，由于边际产量递减规律的作用，劳动的边际产量是逐渐下降的，而资本的边际产量是逐渐上升的。因此，作为逐渐下降的劳动的边际产量与逐渐上升的资本的边际产量之比的边际技术替代率是递减的。边际技术替代率的几何意义是等产量曲线的斜率，由于前者递减，所以等产量曲线凸向原点。

第三，在同一平面图上，可以有无数条等产量线；同一条等产量曲线代表相同的产量，不同的等产量曲线代表不同的产量水平。离原点越远的等产量曲线代表的产量水平越高，离原点越近的等产量曲线代表的产量水平越低。如图5-3所示，Q1、Q2、Q3是三条不同的等产量曲线（Q1 ＜Q2 ＜Q3）。

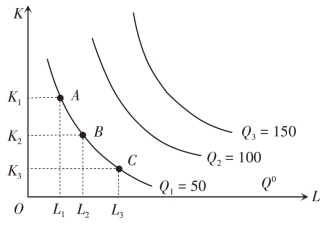
图5-3 等产量曲线组

第四，在同一平面图上，任意两条等产量曲线不能相交。若有相交，则在交点上两条等产量曲线代表了相同的产量水平，这与三个特征相矛盾。(www.daowen.com)

5.4.2 等成本线

等产量线表示的是企业生产同样产量的各种生产要素组合，离原点越远，表示产量越大。然而企业并不能选择任意高度的一条等产量线，因为企业的投入决策要受到来自成本的制约。

等成本线，又称企业预算线，它表明了企业进行生产的限制条件；即在既定成本和生产要素价格条件下，生产者所能购买的两种生产要素数量的最大组合。

M=PL×QL+PK×QK

M 为货币成本，PL、PK 分别为劳动与资本的价格，QL、QK 分别为劳动与资本的购买数量。上式也可以写为：

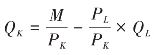
这是一个直线方程式，其斜率为-，横、纵截距分别为和。由此做出等成本线，如图5-4所示。

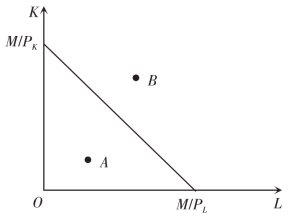
图5-4 等成本线

想一想：等成本线与消费可能线有什么共同之处呢？

在图5-4 中，等成本线上任何一点，都是在货币成本与生产要素价格既定条件下，所能购买的劳动与资本的最大数量的组合。等成本线以内区域中任何一点（如A 点），表示既定的货币成本用来购买该点的劳动与资本的组合以后还有剩余，企业将无法实现产量最大化；等成本线以外区域中的任何一点（如B点），表示既定的货币成本无法购买该劳动和资本组合。

假设各要素价格均不变，如果生产者的货币成本增加（减少），等成本线会平行向右（左）移动，如图5-5（a）所示。

在既定货币成本下，如果其中一种生产要素的价格变动，等成本线会发生旋转。如图5-5（b）所示，假定资本要素价格不变，当劳动要素价格升高时，等成本线绕点A 做逆时针方向旋转到达AB″；当劳动要素价格降低时，等成本线绕点A 做顺时针方向旋转到达AB′。假定劳动要素价格不变，当资本要素价格变化时，等成本线绕点B 做类似旋转，如图5-5（c）所示。

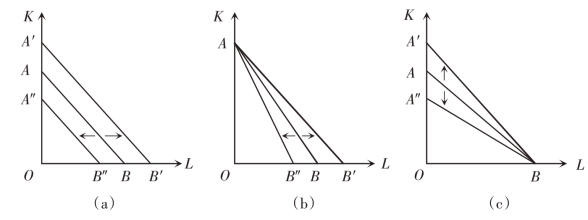
图5-5 等成本线的移动

如果劳动或资本的价格变动，等成本曲线会如何变动呢？（想一想消费可能线的变动）

5.4.3 生产要素组合的最优点选择

无论是等产量线（生产要素在生产过程中的替代关系），还是等成本线（企业所面临的成本约束），都只能反映企业对生产要素组合的可选择范围，并没有说明企业究竟会选择哪种组合进行生产。理性的企业在选择要素组合时，会遵循以下原则：在成本既定的情况下，努力实现产量最大化；或者，在产量既定的情况下，努力实现成本最小化。为得到符合以上原则的最优选择点，我们需要将等产量线与等成本线结合起来进行分析。

同一平面上可以有无数条等产量曲线，那么既定货币成本的等成本线必定其中的一条相切于某一点。在这个切点上，生产要素实现了最适组合；它同时是既定产量下成本最小的生产要素组合，也是既定成本下产量最大的生产要素组合。

图5-6 说明了产量既定条件下成本最小的生产要素组合情况。由于产量既定，所以只有一条等产量曲线。三条等成本曲线中，A″B″代表成本水平最低，但不能生产既定产量Q。为了生产既定产量Q，厂商既可以选择与AB 等成本线的两个交点a 和b 所对应的两种生产要素的组合；也可以选择A′B′代表的成本水平，即选择等产量线和等成本线A′B′的切点E 所对应的生产要素的组合。由于A′B′的生产成本小于AB 的生产成本；显然，厂商将选择E 点进行生产，它所代表的劳动与资本的组合，就是厂商的生产均衡点。

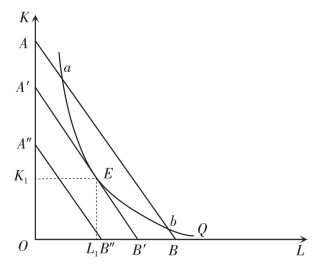
图5-6 产量既定条件下最小的生产要素组合

图5-7 说明了成本既定条件下产量最大的生产要素最优组合。由于成本既定，所以只有一条等成本线。三条等产量曲线中，以Q3代表产量水平最高，但既定的总成本无法生产Q3。等成本线与Q1 有两个交点a 和b，与Q2 有一个切点E；由于Q2 代表的产量水平大于Q1，厂商必然选择要素组合E 生产Q2 以扩大产量。因此，只有E点才是生产要素的最优组合点。

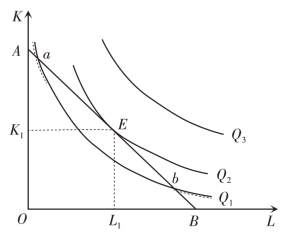
图5-7 成本既定条件下产量最大的生产要素组合

无论是产量既定，还是成本既定，等成本线与等产量曲线的切点E 都是生产者的均衡点。在该点上，等产量曲线的斜率（两种生产要素的边际产量之比）等于等成本线的斜率（两种生产要素的价格之比）。所以，生产者均衡或生产要素最优组合的条件是：

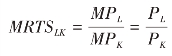
上式又可记作：

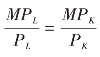
该式的经济含义是：如果劳动和资本两种生产要素可以完全替代，那么厂商可以通过对两种要素投入量的不断调整，使最后一单位货币成本无论用来购买哪一种生产要素所获得的边际产量都相等，从而实现生产要素的最优组合。实际上，这也是关于生产者均衡（两种可变生产要素最适组合）的边际产量分析。

想一想：生产者均衡与消费者均衡的条件有哪些相同之处？

如果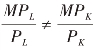，例如：，这说明厂商最后一单位货币成本用来购买劳动所获得的边际产量是购买资本的2 倍，此时厂商就会用劳动来代替资本，使总产量增加。由于边际产量递减规律的作用，劳动投入量的不断增加会使其边际产量递减，资本投入量的不断减少则会使其边际产量递增，直到两者的边际产量和价格之比相等，厂商才会停止用劳动来代替资本，这时便达到了产量最大化。类似，如果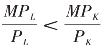，产商可以通过增加资本的投入量，同时减少劳动的投入量，来增加总产量。直到两者的边际产量和价格之比相等，产商才会停止用资本替代劳动，最终实现产量最大化。

在分析两种可变生产要素的最优组合时，无论是使用边际产量分析法，还是使用等产量曲线分析法，得到的结论虽然在表现形式方面有所不同，但本质上是相同的。