（一）层次分析法（AHP）

在许多情况下，当决策者面临多目标、多属性的决策问题时，如果仅仅依靠定性分析和逻辑判断，很难做出正确选择。AHP能在复杂决策过程中引入定量分析，并充分利用决策者在两两比较中所给出的偏好信息进行分析与决策支持。

Seydel（1991）给出了一种基于AHP的确定多风险因素投标报价的方法，具体步骤如下。

步骤1 采用两两比较法确定各个目标之间的相对权重，得到一个权重矩阵：

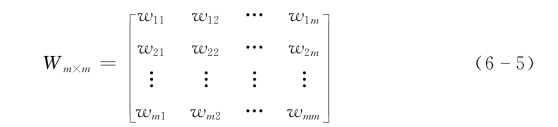
其中，wij=目标Oi/目标Oj，取值范围为（1，3，5，7，9）。

wij=1/wij，i=j时，wij=1，求该矩阵的特征根并进行规范化处理就得到权重向量（λ1，λ2，…，λm）。

步骤2 根据不同的报价值，求出每个目标的各选方案的期望效用，得到一个期望效用矩阵：

其中，eij表示第j个目标（Oj）在报价第i个报价（ri）下的期望效用。对该矩阵的每列进行如下规范化处理：，得到规范化后的期望效用矩阵En×m。

步骤3 计算出不同投标报价下的总期望效用：

其中总效用Ui，最大的投标报价ri为最优报价。

AHP最大的优点在于计算简单与实用，决策过程一目了然。它的缺点在于期望效用矩阵的计算复杂、计算量也大，而且采用两两比较法确定目标之间的相对权重具有较大的主观性。

（二）人工神经网络法

1.人工神经网络的基本原理

人工神经网络是对生物神经网络系统的模拟，其信息处理功能是由网络单元的输出输入特性（激活特性），网络的拓扑结构（神经元的联接方式）所决定的。人工神经网络对问题的求解方式与传统方法不同，它是经过训练来解答问题的。训练一个人工神经网络是把同类一系列的输入例子和理想的输出作为训练的“样本”，根据一定的训练算法对神经进行足够的训练，使得人工神经网络能够学会包含在“解”中的基本原理。训练完成后，该模型可以用来求解相同的问题。

2.基于BP神经网络的风险分析模型的结构

标准的BP神经网络由三个神经元素层次组成，即输入层、隐含层、输出层，层间神经元相互联接，层内神经元之间没有联接。本模型也采用这种结构，输入节点以我们在前面对投标项目风险因素分析的结果为基准，确定为16个输入点。在实际输入时要把对16个风险因素的评价结果量化，输出点数按照对风险度评价的结果确定为5个等级（期望输出为[10000]很高、[01000]较高、[00100]中等、[00010]较低、[00001]很低）。隐含点的数量用公式（n为输入点数，m为输出点数）来确定，N为14。根据前面的分析与设计，用于投标风险分析的神经网络模型为：输入层向量集为{ah}h=1，2，3，…，16；隐含向量集为{bi}i=1，2，3，…，14；输出层向量集为{cj}j=1，2，3，…，5；BP网络模型结构如图6-6所示。

图6-6　投标项目风险分析人工神经网络模型结构图

3.基于BP神经网络风险分析模型的算法

（1）对输入值的处理。由BP网络的响应函数的特性可知，节点输出值的区间为（0，1），所以我们必须对训练样本进行数值处理，使节点的输入输出值限制在（0，1）之间，然后输入网络。本模型的输入值按照下面的方法确定：利用专家打分法对输入因子进行评定，根据因子性能的好坏分成5个等级（很好、好、一般、坏、很坏），量化后依次为5，4，3，2，1；得到输入因子的分值后统一除以5，将其量化为（0，1）区间的数值后输入网络。

该模型各层的初始权值与阈值可以取（0，1）区间内的随机数。

（2）输入、隐含、输出节点的输入值与误差计算。列于BP神经网络模型的输入层神经元，其输入与输出相同，即输入值为z，输出值也为z，下列公式中的f（x）=1/（1+e-x）。

隐含层的节点输出（yi）为

wij为连接权值；θi为节点阈值。输出节点的输出（ol）为

Tlj为连接权值；θi为节点阈值。输出节点的误差δl为

δl=（tl-ol）×ol×（1-ol）

tl为理想输出。

隐含节点的误差δi为

（3）权值（wij，tli）与阈值（θl，θi）的调整。

1）对输出节点的权值修正：

tji（k+1）=tli（k）+ηδlyi

2）对隐含节点的权值修正：

wij（k+1）=wij（k）+Δwij=wij（k）+η′δ′ixj

其中隐含节点误差δ′i中表示输出层节点l的误差δl通过权值tli向隐含节点i反向传播成为隐节点的误差，如图6-7所示。(www.daowen.com)

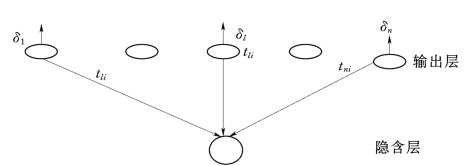
图6-7　误差反向传播示意图

3）对输出节点的阈值修正：

θl（k+1）=θl（k）+ηδl

4）对隐含节点的阈值修正：

θi（k+1）=θi（k）+η′δ′i

4.对基于BP神经网络风险分析模型的训练与检测

利用BP神经网络分析投标项目的风险度可分以下几个步骤：

（1）样本训练。

1）将样本的输入与输出值归一化后，输入网。

2）初始化权值与阈值，该模型各层的初始权值与阈值取（0，1）区间内的随机数。

3）计算各样本输出节点与隐节点的输出值。

4）分别计算样本输出层与隐层的误差。

5）计算总体误差，如果总体误差满足精度要求，则学习停止，否则转入6）。

6）分别修正输出点与隐含点的权值与阈值，转入3）。

当学习结束时，各节点的权值与阈值不再改变，将成为系统内部的知识。

（2）可以再选择1～2个样本来进行检验，如果输出结果误差满足要求，则此模型可以进一步的使用。

基于BP神经网络风险分析模型的计算机程序是用MATLAB5.3开发，可以实现该模型的快速、准确运行，为投标项目的风险分析提供了有效的工具。

（三）模糊评价法

这种方法是将招标工程模型化，抽象成数学模型加量化计算报价。Fayek（1998）研究了在多因素投标报价确定中的应用，并给出了该方法的模型（见图6-8）和相应的应用软件——PRESSTO（Project Estimating and Tendering Tool）。这个方法的具体步骤如下：

图6-8　多风险因素投标报价的模糊评价模型

步骤1 确定n个目标Oi（i=1，2，…，n）以及相应的权重wi（i=1，2，…，n），权重的取值为[0，1]的模糊数。

步骤2 确定m个影响投标报价的因素Fj（j=1，2，…，m）以及每个因素被使用程度的权重Aj（j=1，2，…，m），权重的取值为[0，1]的模糊数。

步骤3 确定每一对（Oi，Fj）（i=1，2，…，n；j=1，2，…，m）对投标报价的影响值，取值范围为[0，1]的模糊数，得到一个In×m矩阵：

步骤4 计算（O，F）之间的模糊关系：注：

步骤5 确定每一对（Oi，Fj）（i=1，2，…，n；j=1，2，…，m）的最优投标报价Mk。令Mk=1.0，则Mk±1=0.8，Mk±2=0.6，以此类推，得到（F，M）之间的模糊关系：注：由于人们对7个以上的备选方案的判定有困难（Saaty，1977），所以把投标报价的备选方案定为6个（M1～M6），其中M1=Mmin，M6=Mmax，Z=（Mmax-Mmin）/5，则有：Mk=Mmin+（k-1）×Z（k=1，2，3，4，5，6）。

步骤6 求模糊关系S（O，F）和R（F，M）的合成Q（O，M）有两种合成方法：

方法（1）：Q（Qi，Mk）=S（Oi，Fj）×R（Fj，Mk）

=max min[S（Oi，Fj），R（Fj，Mk）]

=max min[Sij，R（i×j）×k]，j=1，2，…，m

方法（2）：Q（Oi，Mk）=S（Oi，Fj）×R（Fj，Mk）

=sum min[S（Oi，Fj），R（Fj，Mk）]

=sum min[Sij，R（i×j）×k]，j=1，2，…，m方法（1）中的Q（O，Mk）无需规范化，方法（2）中的Q（O，Mk）需规范化：Q′（O，Mk）=。

步骤7 反模糊处理：为最优投标报价。

模糊技术用于多风险因素投标报价的确定，其优点是以充分利用投标商的经验进行投标报价，其缺点也是显而易见的，那就是这种方法根本没有考虑报价的历史数据的作用。