（一）知识的含义及表示方法

知识：设U≠φ是我们所研究对象组成的有限集合，称为论域。其中的任何子集（∀X⊆U），称为U中的一个概念或范畴。U中的任何概念族（F={X1，X2，…，Xn}）称为关于U的抽象知识，简称知识。

知识库：设一个划分定义为：ζ={X1，X2，…，Xn}，Xi⊂U，Xi≠φ，Xi∩Xj=φ，i≠j，且上的一族划分称为关于U的一个知识库。用K=（U，R）表示，其中R为U上的一族等价关系。

不可区分关系：若P⊆R，且P≠φ，则∩P（P中所有等价关系的交集）也是一个等价关系，称为P上的不可区分关系，记为ind（P），且有表示与等价关系族相关的知识，ind（P）的等价类称为知识P的基本概念或基本范畴。

知识表达系统：知识表达系统用S=（U，A，V，f）来表示，其中U为论域；A为属性的非空有限集合；是属性a的值域；fU×A→V是一个信息函数，它为每个对象的每个属性赋予一个信息值，即∀a∈A，x∈U，f（x，a）∈Va。当系统中属性A=C∪D，其中C为条件属性，D为决策属性时，此系统也称为决策系统。

（二）粗糙集

粗糙集：令X⊆U，R是U上的一个等价关系。当X为R的某些等价类的同时，称X是R可定义的，否则称X是R不可定义的。R可定义集称为R精确集，R不可定义集称为R粗糙集。粗糙集可以用两个精确集表示，即粗糙的下近似和上近似。

下近似：包含在X中的最大可定义集称为X的R下近似：

上近似：包含在X中的最小可定义集称为X的R上近似：

边界域：集合称为X的R边界域；称为X的R正域；称为X的R负域。

近似精度与粗糙度：设集合X是论域U上的一个关于R的粗糙集，定义X关于R的近似精度为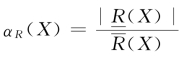，其中X≠φ，|·|表示集合中所包含元素的数目，称集合的基数或势；而定义X的R的粗糙度为ρR（X）=1-αR（X）。

知识表达系统与决策表：(www.daowen.com)

知识表达系统可描述为S=（U，A），其中U为非空有限集，称为对象集；A为非空有限集，称为属性集。

（三）属性约简

约简与核：令R为一族等价关系，R∈R，如果ind（R）=ind（R-{R}），则称R为R中不必要的，否则称R为R中必要的。如果每一个R∈R都为R中必要的，则称R为独立的；否则称R为依赖的。设Q⊆P，如果Q是独立的，且ind（Q）=ind（P），则称Q为P的一个约简。P的核为：core（P）=∩red（P），其中red（P）表示P的所有约简。

相对约简与相对核：令P和Q为U中的等价关系，Q的P正域记为posP（Q），即

令P和Q为等价关系族，R∈P，如果

posind（P）[ind（Q）]=posind（P-{R}）[ind（Q）]

则称R为P中Q不必要的，否则R为P中Q必要的，如果P中的每个R均为Q必要的，则称P为Q独立的。设S⊆P，S为P的Q约简，当且仅当S是P的Q独立子族且poss（Q）=posP（Q）时，P的Q约简简称相对约简。P中所有Q必要的原始关系构成的集合称为P的Q核，简称为相对核，记为coreQ（P），coreQ（P）=∩redQ（P），其中redQ（P）是所有P的Q约简构成的集合。

依赖程度：令K=（U，R）为一知识库，且P，Q⊆R，当

k=γP（Q）=|posP（Q）|/|U|

时，称知识Q是k（0≤k≤1）度依赖于知识P的，记作P⇒kQ。