通常所说的BP模型即误差反向传播神经网络，是神经网络模型中使用最广泛的一类。从结构上讲，BP网络是典型的多层网络，分为输入层、隐层和输出层，层与层之间多采用全连接方式，同一层单元之间不存在相互连接。图5-5给出了一个三层BP网络结构，与多层感知机结构相比，二者是类似的，但差异也是显著的。首先，多层感知机结构中只有一层权值可调，其他各层权值是固定的、不可学习的；BP网络的每一层连接权值都可通过学习来调节。其次，感知机结构中的处理单元为线性输入—输出关系，单元状态为二进制的0或1；而BP网络的基本处理单元（输入层单元除外）为非线性的输入—输出关系，一般选用下列S型作用函数：

图5-5　三层BP网络结构

（一）BP学习算法的过程

提供样本模式对（X t，Y t）（t=1，2，…，T）训练模型。学习的过程就是调整权值Wij和阙值θj，使得实际输出与期望的样本输出之间误差最小。我们选用S型函数，来描述BP学习算法。

（1）初置权值wji（0＜wji＜1）。

（2）正向计算o′j，o′k：

对于每一样本模式t（1≤t≤T），计算隐层各节点输出：

计算输出层各结点输出：

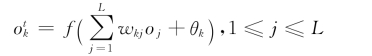
（3）反向计算误差梯度：

计算输出层结点k的δ：

(www.daowen.com)

计算隐层结点j的δ：

（4）调整权值。按下式调整权值，进行修正：

wji（n+1）=wji（n）+ηδjoi+α[wji（n）-wji（n-1）]

其中：η，α是[0，1]间的系数（统称学习参数）。

（5）转向（2）。（2）～（4）完成一轮训练。不断重复这一过程，直到实际输出与期望的样本输出误差足够小为止。

（二）模型的建立

通常，工程项目招标时对投标单元的资格预审概括起来包括以下几方面的内容：投标单位的一般性资料，如公司的名称、国别、性质、注册地址和电话及负责人姓名等；财务情况，主要是近三年来公司经营财务情况，已完成的和未完成部分的合同金额的百分比；工程经历年限，一般不少于2年，工程经历越长越好。施工经验记录，近若干年（如5年或10年）内完成的各类工程（包括类似工程合同经验、类似现场条件合同的经验）的名称、性质、规模、资金等；施工机具设备；拟派往该项目的关键人员和劳务，特别是主要技术人员和项目经理；工程的分包和转包计划，有些项目规定，担任总承包的公司不得转包合同金额的50%以上土建工程给分包人；其他一些情况，如在过去若干年中执行完毕，及目前在建工程合同实施过程中，公司所介入的诉讼或仲裁情况，公司的信誉情况等。

赋予随机初始权值w1，w2，…，w10。根据投标单位资格预审的实际应用情况，输入层前3个因子x1，x2，x3只对隐层第一个因子的输出有贡献，其他7个因子对隐层的第一个因子的输出贡献为0，即权值为0。同样，输入层x4，x5，x6这3个因子只对隐层第二个因子的输出有贡献，对隐层其他因子的权值为0；输入层最后4个因子只对隐层第三个因子的输出有贡献，对隐层其他因子的权值为0。去掉这些权值为0的连接，即得如图5-6所示的简化神经网络模型。在实际应用中，只需输入随机的初始权值，并给定相应数量的训练模式对，采用BP算法进行训练。当学习到满足预定精度要求时便认为网络学习完成，此时的权值便是网络的最终权值。再往训练后的网络中输入测试集即参与资格预审的投标单位各评审因素，便可得到该投标单位的最后综合评定结果。

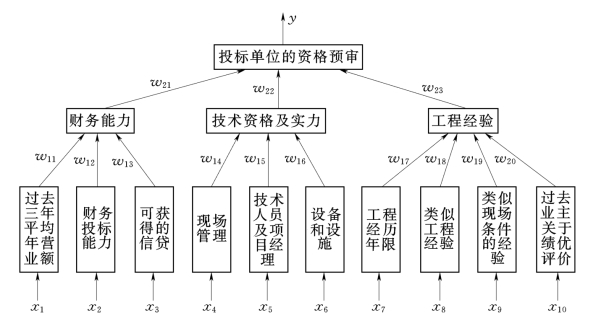
图5-6　资格预审的神经网络模型

输入层因子xi（i=1，2，…，10）即指标量度共有A、B、C、D、E五个标度，分别与定量化取值0.9、0.7、0.5、0.3、0.1相对应，A表示该因子完全满足预定要求，为极端最优状态；E表示该因子完全不满足预定要求，为极端最差状态，见表5-17。指标量度的具体取值应根据资格预审小组对投标单位的具体情况由专家确定。

表5-17　评价因子的取值模式

网络训练时，训练模式对的期望输出即y值可从以往的招投标实际中得到，并进行归一化处理。这样便可得到0.0～1.0的一个值作为最后的综合评定结果，资格预审小组可根据具体工程项目和投标单位的情况，确定通过资格预审的最低指标，如取y0=0.6，即当输出信号y=0.6时则认为该投标单位通过资格预审；反之则认为该投标单位资格预审不合格。