（一）阶梯状层次结构的建立

在招投标工作中，每个施工企业都面临着多家企业竞争、施工机械、业主等多方面因素的影响，在同一工程的不同阶段，施工企业也面临着投标哪一个施工阶段的问题，等等。在利用层次分析法解决这一问题时，首先就要建立一个阶梯状层次结构，它由目标层、一个或多个因素层和方案层组成。其具体结构如图5-3所示。

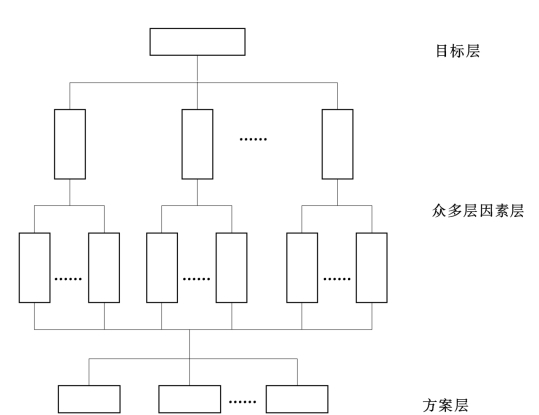
图5-3　阶梯状层次结构

（二）构造判断矩阵

任何系统分析都以一定的信息为基础。AHP的信息基础主要是人们对每一层次各因素的相对重要性给出的判断，这些判断用数值表示出来，写成矩阵形式就是判断矩阵。判断矩阵是AHP工作的出发点，构造判断矩阵是AHP的关键一步。

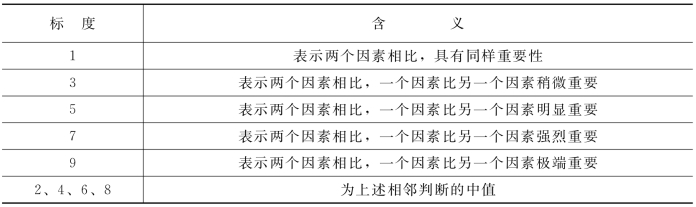
判断矩阵表示针对上一层次某因素而言，本层次与之有关的各因素之间的相对重要性。判断矩阵是定性过渡到定量的重要阶段，其重要程度是用1～9来进行标度，具体见表5-7。

表5-7　标度数的含义

判断矩阵的构造：设某层有n个因素，X={x1，x2，…，xn}，要比较它们对上一层的影响程度，确定在该层中相对于上一层所占的比重。用aij表示第i个因素相对于第j个因素的比较结果，则

当判断矩阵A的阶数较高时，用定义求A的特征值和特征向量很困难，我们可选用一些近似的计算方法，其依据的原理是当A为正矩阵时，A的最大特征值为正值，相应的特征向量也为正值，且有

为了使最大特征值对应的特征向量作为被比较的因素对上层某因素影响程度的权向量的一致性程度有所判断，所以我们要进行一致性检验。(www.daowen.com)

引入一致性指标CI=（λmax-n）/（n-1），其中n为A的对角线元素之和，也为A的特征根之和。

由于矩阵的阶数不同，满足一致性的难易程度也不同，故引入随机一致性指标。

定义随机一致性指标RI：随机构造500个判断矩阵A1，A2，…，A500，得到的相应一致性指标为CI1，CI2，…，CI500，则。

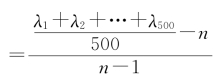随机一致性指标RI的值见表5-8。

表5-8　随机一致性指标RI的值

当一致性比率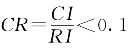时，认为不一致程度在容许范围内，可以用归一化的特征向量作为权向量，否则，应该重新构造判断矩阵A，然后再重新进行判断。

（四）层次总排序计算及一致性检验

层次总排序：确定某层所有因素对于总目标相对重要性的排序权值过程。

设因素层A共m个因素A1，A2，…，Am，对总目标G的排序为a1，a2，…，am，方案层B的n个元素对A中Aj的层次单排序为b1j，b2j，…，bnj（j=1，2，…，m），则B层第i个元素对总目标的权值为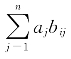，详见表5-9。

表5-9　层次总排序计算

总排序一致性检验：

当层次总排序的一致性比率时，认为层次总排序满足要求，根据总排序作出决策。

其中CIi，RIi分别为B层B1，B2，…，Bn对上层A中的元素Ai的层次单排序一致性指标和随机一致性指标（i=1，2，…，m）。