在招投标中，可把其他竞争对手看成一个人，这时局中人为我方和其他竞争对手。局中人之间报价的竞争，实际上就是连续对策问题。但在实际工作中可以将拟定报价的范围每隔一定的百分点适当划分为若干个方案，于是连续A对策又变成非连续对策。

设局中人Ⅰ有m个纯策略α1、α2、α3、…、αm，局中人Ⅱ有n个纯策略，β1、β2、β3、…、βn，则局中人Ⅱ的策略集分别为

S1={α1、α2、α3、…、αm}；

S2={β1、β2、β3、…、βn}；

当局中人Ⅰ选定纯策略αi和局中人Ⅱ选纯策略βj后，就形成了纯局势（αi，βj），这样的纯局势共有m×n个。对任一局势（αi，βj），记局中人Ⅰ的赢得值（或失分值）为αij，则称

为局中人Ⅰ的赢得矩阵亦称矩阵对策模型。

（一）最佳标底矩阵

一般情况下，我们不能按式（5-6）来确定报价。因为这时没有考虑到当时对手策略变化时所选的策略是否最优。因此必须研究多个决策者的策略相互影响时，投标方如何作出明智的决策。

根据式（5-4），当局中人Ⅰ选定报价wi和局中人的报价为后，就形成了一个纯局势），将其各种可能结果列成m×n矩阵，即最佳标底矩阵。

其中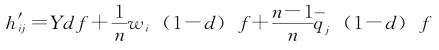，(www.daowen.com)

（i=1，2，…，m；j=1，2，…，n）

（二）报价误差矩阵和报价分值误差矩阵

将局中人Ⅰ报价分别减去最佳标底矩阵的元素，即得报价误差矩阵。

报价分值误差矩阵是在报价误差矩阵的基础上演变而来的，将误差矩阵中的每个元素分别乘以扣分系数lij（i=1，2，…，m；j=1，2，…，n）即得报价分值误差矩阵，一般情况是：

①当wi-h′ij＞0时 h′j=-2 （即超1%扣2分）

②当wi-h′ij＜0时 h′j=1 （即低1%扣1分）

（三）对策矩阵

对策矩阵的策略是：在报价分值误差矩阵的每一行元素中，找出一个最不利局中人Ⅰ的元素（绝对值最大的元素），然后将这些元素排成一个矩阵，再从该列矩阵中选出最小的元素，这个矩阵就称为对策矩阵。设这个最小的元素为，则

所对应的行，即为局中人Ⅰ的最佳报价方案。对策论原理的实质是：以不变应万变，以求得对局中人Ⅰ的最不利因素减小到最低限度。