（一）模型的建立

把某个竞争对手的投标历史数据拿出来研究分析，选取工程项目代表性的工程量作为自变量，相应的工程价格作为因变量，利用数理统计方法中的多元回归模型进行预测。

多元回归数学模型的建立：

y=b0+b1 x1+b2 x2+…+bkxk+ε ε～N（0，ο2）

式中 y、bi——估计量，分别表示竞争对手的可能报价和取费水平；

ε——估计的偏差。

对于bi和ε的估计，可以通过竞争对手的投标历史数据进行计算，在软件设计中，每个单位设一个数据库，通过积累资料，逐渐达到预想的效果。

样本指竞争对手的历史资料，Y表示相应的投标价，下标k表示引入计算的参量数目，n表示所收集到的工程样本数。如果

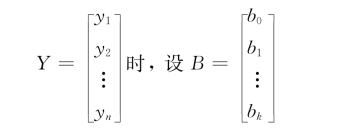
根据矩阵运算法则，得(www.daowen.com)

B=（X T X）-1 X T Y

即得B的估计，则有

对于施工企业的投标报价，要求能够比较准确的估计项目的报价，需要考虑更多因素的影响，这就要求参量的多元化，此模型能够满足分析多因素同结果间的关联关系。

（二）实例分析

某企业预投标某工程，现搜集已有工程的数据，按照洞室开挖量、混凝土工程量、钢筋安装量作为参量进行计算，为了便于计算，需要先将数据进行同一化处理，即将洞室开挖量除以1000000，将混凝土浇筑量、钢筋安装量分别除以10000，得到的数据见表5-4。

表5-4　三个工程的数据

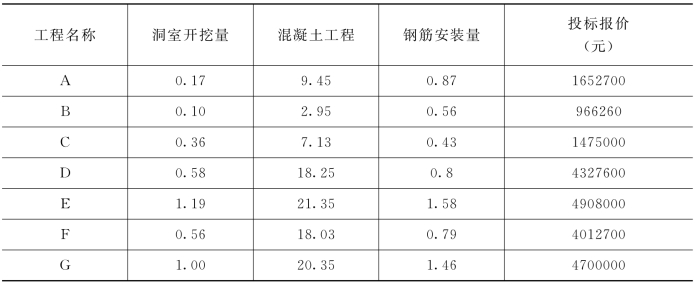
根据上述模型，若已知现有工程的三个参数，则可以计算现有工程的报价。