1.事件集、对策集和局势集的确定

某基础工程公司欲对四项工程项目进行选择和评价，以确定投标项目。选择工程项目为事件，事件集A={a1，a2，a3，a4}，式中a1，a2，a3，a4分别为工程项目甲、工程项目乙、工程项目丙、工程项目丁。参加投标和不参加投标为决策b1，b2，则有对策集B={b1，b2}，局势集S={Sij=（ai，bj）|ai∈A，bj∈B}，式中S11=（a1，b1）={工程项目甲，参加投标}，S12=（a1，b2）={工程项目甲，不参加投标}，其余类推。

2.目标及样本效果的确定

基础工程施工企业投标决策目标的选择一般考虑影响投标的风险因素。本次投标选择以下6（A=6）个目标进行决策（以下分别用u（1），u（2），u（3），u（4），u（5）和u（6）表示）。

u（1），企业中标后的收益值（万元），指标值越大越好，为极大值目标，这一目标通过绘制决策树进行分析和取值。过程是首先把各工程中标后可能得到的收益值或损失值标注在决策树概率分支的末端，称为期望损益值；再把工程中标后可能出现的经营概率标注在概率分支上（见图3-2），计算每一个决策点的期望值：

式中 E（xi）——第i个方案的n个损益值的期望值，是按概率分布计算的加权平均值；

pij——第i个方案的第j个损益值发生的概率；

xij——第i个方案的第j个损益值；i=1，2，…，m（m为待决策的方案，实例计算中m=4）；j=1，2，…，n（n为经营情况分类。

实例计算中有经营好、经营一般和经营差三种情况，n=3。标注于最后一层概率结点上方的期望值E（xi）即为企业中标后的收益值（图3-2）。不参加某工程项目的投标时，收益值为0，由此确定了u（1）的实测效果值。

u（2），投标风险值，指标值越小越好，为极小值目标。投标风险值用标准离差率wi表示，它是标准差与期望值的比值，即wi=οi/E（xi），其中，οi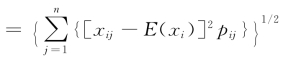（标准差），各符号含义与E（xi）公式相同。标准差是反映不同条件下损益值和期望值之间离散程度的指标，标准差越大，概率分布越分散，投标风险程度也越大，但标准差不能用于比较不同方案的风险程度。在标准差相同的情况下，因为期望值不同，风险程度也不同，所以用标准离差率（风险值）来表示企业不同收益值的风险程度。将标准离差率（风险值）的计算结果标注于决策树最后一层概率结点的下方（图3-2）。不参加某工程项目投标时，风险值为0，u（2）为极小值目标，取下限效果测度，计算时就出现了分母为0的情况，为了避免这种情况出现，将u（2）中不参加投标的风险值近似取为0.01，由此可以确定u（2）的实测效果值。

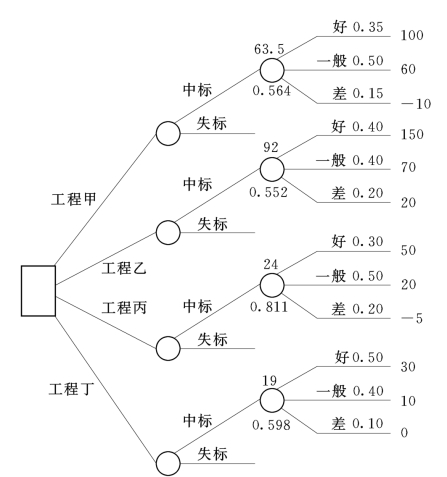
图3-2　工程投标决策树

u（3），投标过程中的风险损失值（万元），为极小值目标。参加投标时，根据基础公司投标预算及拟投标工程项目情况确定，本身为负值或0，为计算方便，取其绝对值为u（3）的实测效果值。同理，为避免出现分母为0的情况，将u（3）中不参加投标的风险损失值近似取为0.01。

u（4），机械设备条件和技术人员条件，用机械设备满足率（现有机械设备占工程所需机械设备的百分比）和技术人员满足率（现有技术人员数量占工程所需技术人员数量的百分比）表示。首先赋予两因素一定权值，若机械设备条件的权值为0.6，则技术人员条件的权值为0.4，然后，计算它们的加权平均值，以这一加权平均值作为u（4）的实测效果值。本次实例计算中，两因素的权值都确定为0.5，为极大值目标。根据基础公司设备及技术人员情况确定u（4）的实测效果值。

u（5），投标或中标后可能带来的长期效益。今后给企业带来的影响和机会，为极大值目标。定性指标，可根据若干名专家对企业中标后带来的长期效益进行评价，取得量化值，得到u（5）的实测效果值。

u（6），施工经验。以往工程业绩，特别是相近项目的施工业绩（能力），为极大值目标。定性指标，可根据专家评价进行量化，得到u（6）的实测效果值。(www.daowen.com)

作为一个大型企业，长期效益和施工经验相对稳定，具有一定的客观性，不需要每次投标时都重新确定。根据某基础公司的具体情况，确定各局势在决策目标A（A=1，2，…，6）下的样本效果。

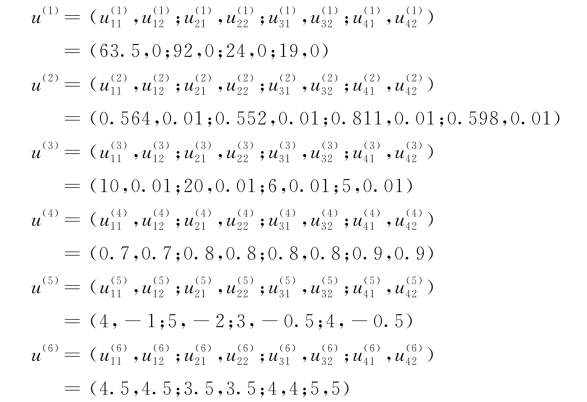
3.效果测度的计算

对于极大值目标，取上限效果测度。例如，对于u（1）取上限效果测度，效果测度r11的计算过程为，则63.5/92=0.6902，同理，可得到各目标的效果测度矩阵，其结果如下：

D（1）=（0.6902，0；1，0；0.2609，0；0.2065，0）

D（2）=（0.0177，1；0.0181，1；0.0123，1；0.0167，1）

D（3）=（0.001，1；0.0005，1；0.0017，1；0.002，1）

D（4）=（0.7778，0.7778；0.8889，0.8889；0.8889，0.8889；1，1）

D（5）=（0.8，-0.2；1，-0.4；0.6，-0.1；0.8，-0.1）

D（6）=（0.9，0.9；0.7，0.7；0.8，0.8；1，1）

4.非等权目标综合效果测度的计算

根据目标的重要性不同，将目标1～6赋权值，得到目标权向量ρ=（0.23，0.23，0.15，0.14，0.15，0.1）。因此，多目标的加权局势决策综合矩阵为

D（∑）=0.23D（1）+0.23D（2）+0.15D（3）+0.14D（4）+0.15D（5）+0.1D（6）

=（0.4818，0.5489；0.6182，0.5145；0.3572，0.5695；0.4113，0.6015）

5.局势决策

根据多目标加权局势决策综合矩阵，选择最大的综合效果测度值为最优局势。按行选择最优局势为S12，S21，S32，S42，列最优局势为S21，S42，综合分析得到最优局势为S21，S42，即{工程项目乙，参加投标}、{工程项目丁，不参加投标}。因此，企业应该优先选择工程项目乙进行投标，最不应该投标的是工程项目丁。如果企业的工作量不饱满，人力、物力、财力相对过剩，为保证企业闲置资源的利用，满足企业职工的基本生活保障，则需提供一个后备投标项目作为选择，此时，可以选择S11局势（S11=（a1，b1）={工程项目甲，参加投标}），即选择工程项目甲进行投标。