确定权重分配的方法很多，基于信息基础，可以选择定性经验的特尔菲法，精确的定量数据处理的主成分分析法，以及定性定量结合的AHP方法等确定权重。下面介绍几种常用的权重确定方法。

（一）层次分析法AHP（Analytical Hierarchy Process简称AHP）

层次分析法是美国学者于20世纪70年代提出的，它是用一定标度把人的主观判断进行量化，将定性问题进行定量分析的一种简单而又实用的多准则评价决策方法。用层次分析法作系统分析，首先要把问题层次化。根据问题的性质和要达到的总目标，将问题分解为不同的组成因素，并按照因素间的相互关系影响以及隶属关系将因素按不同层次聚集组合，形成一个多层次的分析结构模型。并最终把系统分析归结为最低层（供决策的方案、措施、指标等），相对于最高层（总目标）的相对重要性权值的确定或相对优劣次序的排序问题。层次分析法目前已在各个领域获得广泛的应用，它同时也是求得权重的一个比较有效的方法。

1.层次分析法的优点

（1）将定性的判断与定量的分析相结合。

（2）它符合人类对事物作评判决策时的思维特性：分解——判断——综合。能够利用领域中的专家经验、知识和直觉，通过两两比较的方法，确定各因素之间的关系。

2.层次分析法的步骤

（1）建立层次结构模型。应用层次分析法分析问题时，首先要对问题有明确的认识，弄清问题的范围，所包含的因素，因素之间的相互关联，隶属关系，最终所要解决的问题。根据对问题的初步分析，将问题包含的因素按照是否共有某些特性将它们聚集成组，并把它们之间的共同特性看作系统中新的层次中的一些因素，而这些因素本身也按照另外一组特性被组合，形成另外更高层次的因素，直到最终形成单一的最高因素，这往往可以视为我们决策分析的目标。这样即构成由最高层，若干中间层和最低层排列的层次分析结构模型。

（2）构造判断矩阵。任何系统分析都以一定的信息为基础，层次分析法的信息基础主要是人们对于每一层次中各因素相对重要性给出的判断。这些判断通过引入合适的标度用数值表示出来，写成判断矩阵（见表3-1）。判断矩阵表示针对上一层次某因素，本层次与之有关因素之间相对重要性的比较。假定A层因素中ak与下一层次中的B1，B2，…，Bn有联系，可以构造如下判断矩阵。

表3-1　判断矩阵表

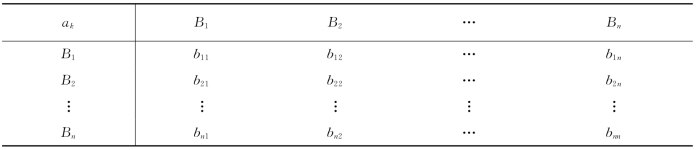
该矩阵有如下性质：bij=1；bij=1/bji；bij≥0（i，j=1，2，…，n）

在层次分析法中，为了使决策判断定量化，形成上述数值判断矩阵，可采用A.L.Satty的1～9标度方法，见表3-2。

表3-2　判断矩阵标度及其含义

（3）计算判断矩阵的最大特征根及其对应的特征向量。判断矩阵进行计算，方法有求和法和方根法，本文采用较为简单的方根法。

1）计算判断矩阵每一行各元素之乘积，即

（4）一致性检验。在层次分析法中，为了形成判断矩阵，引入了1～9标度方法，这就使得决策者判断思维数学化。这种将判断思维数学化的方法大大简化了问题的分析，还有助于决策者检查并保持判断思维的一致性。

在层次分析法中引入判断矩阵最大特征根以外的其余特征根的负平均值，作为度量判断矩阵偏离一致性的指标。

1）计算判断矩阵的最大特征根λmax：

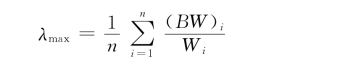
2）计算判断矩阵一致性指标CI：

3）为了度量不同阶判断矩阵是否具有满意的一致性，我们还需引入判断矩阵的平均随机一致性指标RI值。对于1～9阶判断矩阵，RI值见表3-3。

表3-3　平均随机一致性指标

在这里，对于1，2阶判断矩阵，RI只是形式上的，因为1，2阶判断矩阵总具有完全一致性。

4）计算判断矩阵的随机一致性比率CR：

当阶数大于2时，判断矩阵的一致性指标CI与同阶平均随机一致性指标RI之比称之为随机一致性比率，记为CR

（二）德尔菲法（Delphi method）

德尔菲法，又名专家调查法，是确定权数常用的方法，由美国兰德公司于20世纪40年代末提出。它是依据若干专家的知识、经验、信息和价值观，对已拟出的评价指标进行分析、判断、权衡并赋予相应权值的一种调查法，一般需经过多轮匿名调查，在专家意见比较一致的基础上，经组织者对专家意见进行数据处理，检验专家意见的集中程度、离散程度和协调程度，达到要求之后，得到各评价指标的初始权重向量。

(www.daowen.com)

再对w*作出归一化处理，获得各评价指标的权重向量：

（三）熵值法

1.熵与熵值函数

熵（Entropy）原是统计物理和热力学中的一个物理概念，在热力学中熵指一个热力系统在热功转化过程中，热能被有效利用的程度。一个热力系统的熵值大，表示系统的能量可利用的程度低；熵值小，能量可利用程度高。

在统计物理中，熵是分子运动无序度的度量，熵值大，表示系统分子运动的无序度高。在孤立系统中，分子运动的无序度会由低状态向高状态自发进行，要想使系统由高无序状态向低无序状态转化，必须有外力作用。从微观角度，系统的熵值可从分子排列方式的统计中得出。设系统内有两种物质（二元系统），1物质有n1个分子，2物质有n2个分子，该系统的熵值可由波尔兹曼（Boltgman）公式计算：

E是系统（n1+n2）个分子的总熵值，除以分子总数，使得到系统的单位熵值

2.信息系统的熵值函数

在信息系统中的信息熵是信息无序度的度量，信息熵越大，信息的无序度越高，其信息的效用值越小；反之，信息的熵越小，信息的无序度越小，信息的效用值越大。

在综合评判中，运用信息熵评价所获得的系统信息的有序程度及信息的效用值是很自然的，统计物理中的熵值函数形式对于信息系统应是一致的。

3.综合评判中信息熵值及权重函数

对于所讨论的模糊综合评判模型，已获得m个样本的n个评价指标的初始数据矩阵X={Xij}m×n，由于各指标的量纲、数量级及指标优劣的取向均有很大差异，故需对初始数据做标准化处理。

由于信息熵ej可用来度量j项指标的信息（指标的数据）的效用价值，当完全无序时，ej=1，此时，ej的信息（也就是j指标的数据）对综合评判的效用值为零。因此，某项指标的信息效用价值取决于该指标的信息熵ej与1的差值hj。

hj=1-ej

可见，利用熵值法估算各指标的权重，其本质是利用该指标信息的价值系数来计算的，其价值系数越高，对评价的重要性就越大（或称对评价结果的贡献越大），于是j项指标的权重为

（四）模糊聚类分析法

当若干评价指标具有模糊性时，可采用模糊聚类分析法，对指标做模糊分类，并给出分类的权重和排序，其方法如下。

取评价指标体系为论域U={u1，u2，…，ui，…，um}，其中任一指标ui由n个样本隶属度标证，即

ui={xi1=μ1（ui），xi2=μ2（ui）…，xij=μj（ui），…，xin=μn（ui）}

于是得到评价系统的初始化数据矩阵X：

X={xij=μj（ui）}m×n（i=1，2，…，m；j=1，2，…，n）

并进一步提到标准化数据矩阵Y：

Y={yij}m×n

其中

第二步，列出论域U中所指标的序偶（ui，uk），采用数量积分法计算所有序偶的模糊相似系数，得到论域U上的一个相似关系矩阵～R：

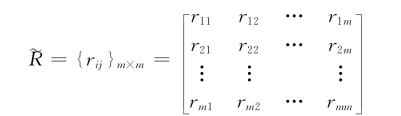
其中

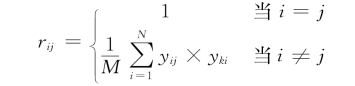
式中，正常数M满足M≥max（yij|i=1，2，…，m；j=1，2，…，n）。第三步，计算的模糊等价矩阵，使其具备自发性、对称性和传递性。为此对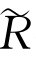做自乘运算；，直到出现，这时，，为模糊等价关系矩阵。

第四步，计算～R*在不同阈值下（λ）的截矩阵（布尔矩阵），对一系列截矩阵做分析可得到评价指标重要程度的分类。一般情况下，随λ由小到大变化，对指标的分类由少到多，为尽可能区分出各评价指标的重要程度，应选取较大的λ值，以便于对评价指标的重要程度做分类和排序，作为进一步确定各指标权重的基础。