【例2-14】考虑投资兴建一个旅游点，选择一个最理想的地点就是决策目标。现在有三个地点D1、D2、D3可供选择。评选的标准有6个：

A1：古迹的吸引力；

A2：名胜风光的条件；

A3：费用程度；

A4：生活条件；

A5：交通条件；

A6：接待工作的水平。

两两对比的判断矩阵列于表2-24～表2-30，试对此问题决策。

表2-24　两种对比（一）

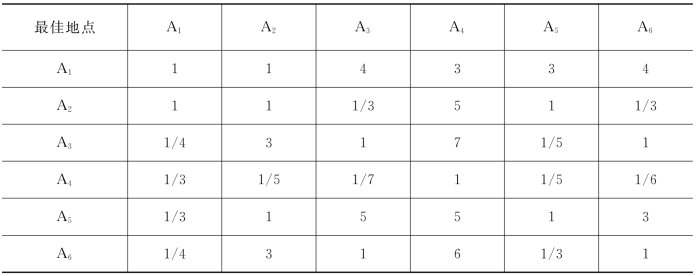
表2-25 两两对比（二）

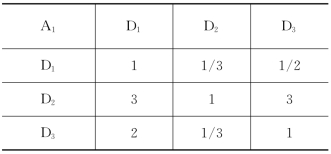
表2-26 两两对比（三）

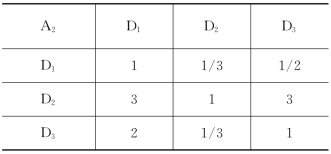
表2-27　两两对比（四）

(www.daowen.com)

表2-28　两两对比（五）

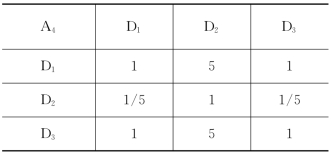
表2-29　两两对比（六）

表2-30　两两对比（七）

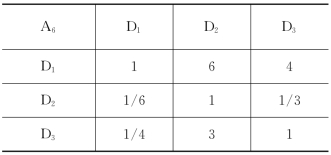
解：这是一个多目标决策问题，用层次分析法决策。

首先，建立层次模型。有三层：总目标层是选择地点；中间层是三个目标；最底层是三种方案。各层判断矩阵已经给出，下面确定各层权重（用列向量表示）。第一层到第二层：矩阵归一化然后每行相加归一化得到权重W（0）。

第二层到第三层：A1-A6与各方案的权重分别为W（1）-W（6）。一致性检验相关数据结果依次为

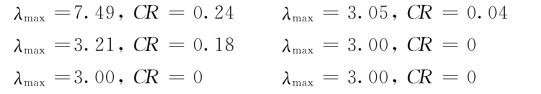
各判断矩阵一致性检验系数均小于0.1，认为判断矩阵具有满意的一致性。

最后，各方案对总目标的权重为

W=（W（1）W（2）W（3）W（4）W（5））W（0）=（0.37，0.38，0.25）

第二个方案的权重最大，因此选择地点D2最佳。

λmax=3.05，CR=0.04