在目标决策中存在许多“亦此亦彼”的模糊现象,这类现象是否符合一定的概念也是不容易确定的。在多目标决策活动中,尽管决策的目标十分明确、具体,但都是事先不能确定,均有一定的模糊性。研究模糊性问题不能用传统的数量分析法,而需要用模糊决策法进行分析。
模糊决策,就是对事先难以确定的决策目标的模糊性,用定量的方法作出决定。要将一些模糊目标转化成为决策评价的标准,必须通过模糊决策数量分析的方法才能解决。
(一)模糊集合概念
正像用经典集合理论来描述非模糊现象一样,对模糊现象的研究则是利用模糊集合理论。
设X为一基本集,若对每个x∈X都指定一个数![]() ,则定义模糊子集
,则定义模糊子集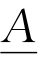

式中,![]() 称为
称为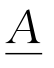 的隶属函数,
的隶属函数,![]() 称为元素xi的隶属度。
称为元素xi的隶属度。
(二)隶属函数的确定
这里仅介绍几种常用的方法,不同的方法结果也会不同,判别所确定的隶属函数的好与不好的标准是看它是否符合实际要求。
1.模糊统计法
在有些情况下,隶属函数可以通过模糊统计试验的方法来确定,这是确定隶属函数的主要方法。其思想是通过对足够多人的调查统计,对要确定的模糊概念在讨论的基本集中逐一写出定量范围,再进行统计处理,以确定能被大多数人认可的隶属函数。这实际上是对人群主观看法的统计处理。已有不少国内外学者进行了这方面的研究、确定在一定条件下随着调查人数的增加,各个元素隶属度都趋于一个稳定值。
2.例证法
例证法是Zadeh在1972年提出的,主要思想是从已知有限个![]() 的值,来估计基本集X上的模糊集合
的值,来估计基本集X上的模糊集合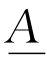 的隶属函数。例如基本集X是全体人类,
的隶属函数。例如基本集X是全体人类,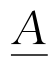 是“高个子的人”,显然
是“高个子的人”,显然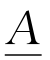 是模糊集合。为了确定
是模糊集合。为了确定![]() ,可以先给出一个高度h值,然后选定几个语言真值(即一句话真的程度)中的一个,来回答某人高度是否算“高”。如语言真值分为“真的”、“大致真的”、“似真又似假”、“大致假的”、“假的”。然后,把这些语言真值分别用数字表示为1、0.75、0.5、0.25、和0。将n个不同高度h1,h2,…,hn作为样本进行询问,就可以得到
,可以先给出一个高度h值,然后选定几个语言真值(即一句话真的程度)中的一个,来回答某人高度是否算“高”。如语言真值分为“真的”、“大致真的”、“似真又似假”、“大致假的”、“假的”。然后,把这些语言真值分别用数字表示为1、0.75、0.5、0.25、和0。将n个不同高度h1,h2,…,hn作为样本进行询问,就可以得到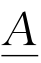 的隶属函数
的隶属函数![]() 的离散表示法。
的离散表示法。
3.专家经验法
根据专家的实际经验,确定隶属函数的方法称为专家经验法。即专家的实际经验和必要的数学处理相结合来确定隶属函数。例如在各种体育比赛中,裁判员的评分就是他们大量的丰富的实际经验的综合结果。
在许多情况下,经常是初步确定粗略的隶属函数,然后再通过“学习”和实践检验逐步修改和完善,而实际效果正是检验和调整隶属函数的依据。
(三)几种常用的隶属函数(www.daowen.com)
隶属函数形式有多种,可根据实际要求来确定。在实际应用中为方便起见,常采用三角形、正态形、梯形。以下是这3种隶属函数的解析式及曲线图。
(1)三角形。解析式为
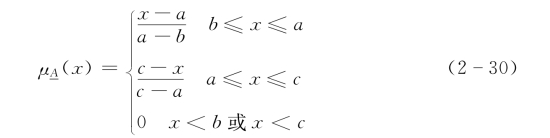
隶属函数曲线图如图2-7所示。
(2)正态形。解析式为
![]()
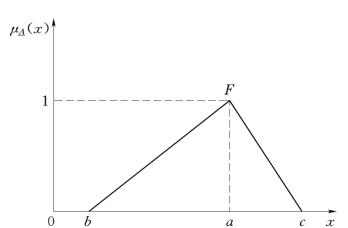
图2-7 三角形隶属函数
隶属函数曲线图如图2-8所示。
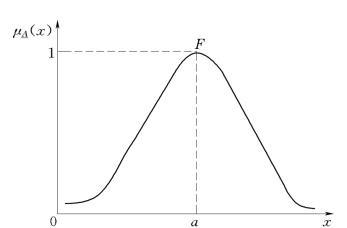
图2-8 正态形隶属函数
(3)梯形。解析式为
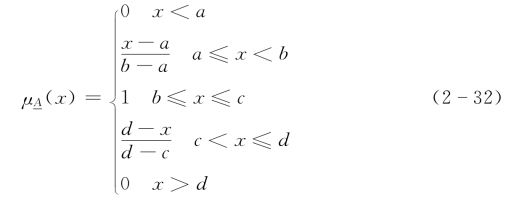
隶属曲线图如图2-9所示。
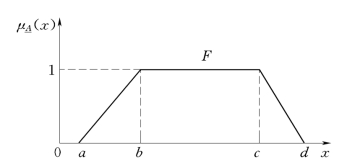
图2-9 梯形隶属函数
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





