在风险型决策分析中，对自然状态发生的可能性估计（概率分布）得正确与否，直接决定着其后所作出决策的优劣。下面我们将介绍如何改进对自然状态的概率分布的初步估计（先验分布），并在此基础上作出贝叶斯（Bayes）决策。

（一）先验分布

在通过试验收集有关自然状态的新信息之前，决策人根据已掌握的信息所确定自然状态的概率分布称为有关自然状态的先验分布。先验分布通常又有客观的先验分布与主观的先验分布之别。

1.客观的先验分布

根据某些客观的情报或证据，甚至能通过在过去相同条件下的大量重复试验的经验资料来确定的自然状态的概率分布称为客观的先验分布。例如，我们可以用某一段时期内每批产品所包含的不合格产品数目来估计该产品不合格品率的概率分布；用某城市过去历年秋季火灾的次数来估计明年秋季火灾次数的概率分布，等等。对这些自然状态先验概率的估计或指定是根据某些客观的情报或证据得出的，故称其为客观先验分布。

2.主观的先验分布

不能根据客观的情况或证据以及通过过去相同条件下的大量重复试验，而是通过主观上的一些关于自然状态的经验、知识来确定的自然状态的概率分布称为主观先验分布。我们举一例来说明决策者如何指定主观的先验概率分布。假定有个决策问题，其自然状态为未来6个月内的贷款利率变化，设有2种可能的自然状态，分别用S1和S2表示。

S1：利率将下降；

S2：利率将维持不变或上升。

如果能获得此自然状态的概率分布，即S1和S2出现的概率，就可以利用它作出可靠的决策。假如决策者已有从事工商企业研究多年的经历，对于预测未来的经济状况的变化，他就有丰富的经验，那么他可以运用过去观察到的经济状况与贷款利率之间的关系，推测S1和S2发生的概率，而不仅仅是凭预感或直觉去指定这些概率。如果决策者不满足于单凭他自己拥有的知识去指定先验概率，则他还可以再请教一些银行家、经济学者、市场研究机构等，综合他们的意见后再来指定这些先验概率。

无论是客观的还是主观的概率分布，都可以当做一般的概率分布，采用概率运算的一系列法则进行运算。

（二）后验概率分布与贝叶斯（Bayes）定理

在作决策分析时，根据试验或调查所获得的情报，对先前确定的先验概率分布加以修正，而得到关于自然状态的新的概率分布，我们称之为后验分布。

在实际决策中，由于直接观察所判断状态变量得到的先验分布往往是不准确的，因此，为了对自然状态有更多了解，常常需要进行统计调查以改善自然状态的先验分布。观察另一个与该状态变量有关的随机变量x，获得补充信息，利用下面我们介绍的贝叶斯定理将先验分布和补充信息结合起来，便获得了优越于先验分布的有关自然状态的后验概率分布。后验分布可以用来作出较为正确的决策。

贝叶斯定理：设自然状态θ有n种；P（θi）表示自然状态θi发生的先验概率分布；P（x|θi）表示在自然状态为θi的条件下，调查结果为x的概率；而P（θi|x）表示在调查结果为x的条件下，自然状态为θi的概率。通过调查得到结果x，其中包含了有关自然状态的信息，将这个补充信息结合到先验分布P（θi）中，便获得了有关自然状态的后验概率分布：

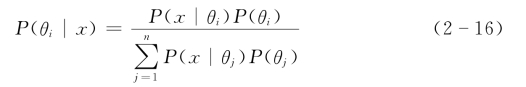
（三）贝叶斯风险

为了衡量所采用行动方案的损益，需要引进贝叶斯风险的概念。

假设自然状态θ有n个，即θ1，θ2，…，θn；行动方案a有m个，即a1，a2，…，am；损失函数为R（θ，a）。设补充情报为x，对某一决策方案δ（x），x的值一旦确定，则对应的决策方案δ（x）也就确定了，对应的损失为R[θ，δ（x）]。

在自然状态θ取定为θi的条件下，x仍然是一随机变量，δ（x）也是一随机变量，此时衡量决策方案δ（x）的损益应为期望损失：

表示在状态θi下，决策方案的风险值，或者说是当出现不同情报值时，按决策方案采取行动的平均损失，成为风险函数。

在不同状态下，同一决策方案的风险值不一样，一个决策方案的优劣应由在不同状态下风险值的期望值来衡量，即

Q（δ）成为决策方案δ（x）的贝叶斯风险，它反映决策方案的平均损失。

（四）最佳决策方案

贝叶斯决策分析的核心问题是求解最佳决策方案，最佳决策方案应该是使贝叶斯风险最小的决策方案。对任何一个决策问题，求解最佳决策方法都有两种基本的方法：第一种方法称为正序分析；第二种称为反序分析。

1.正序分析

即列举出所有可能出现的抽样结果x及所有可能的决策方案δ（x），针对某一方案δ（x），计算其贝叶斯风险Q（δ），比较各种方案的贝叶斯风险大小，使Q（δ）最小的δ（x）即为最佳决策方案。

2.反序分析

利用正序分析的方法求解最佳决策方案常常使得计算量过大，为了减少计算量，考虑采用反序分析。

注意到贝叶斯风险

那么如果某个δ（x）使每个x下R[δ（x）]均为最小，就能使贝叶斯Q（δ）风险达到最小，这个δ（x）就是最佳决策方案。

这里的问题就是求解δ（x）使得每个x下的R[δ（x）]达到最小。

反序分析的过程为：针对所有可能出现的抽样结果，分别计算各自然状态的后验概率，利用这些概率求出各行动方案的后验损失值，比较后验损失值的大小，选择各种抽样结果下的最佳行动方案，综合成最佳决策方案。

【例2-13】某建材厂计划生产某一种新产品，产品的销售情况有好（θ1）、中（θ2）和差（θ3）三种，据以往的经验，估计三种情况的概率分布和利润见表2-18。

表2-18　三种情况的概率分布和利润(www.daowen.com)

为进一步摸清市场对这种产品的需求情况，工厂通过调查和咨询等方式得到一份市场调查表。销售情况也有好（H1）、中（H2）、差（H3）三种，其概率列在表中。

假设得到市场调查表的费用为0.6万元，试问：

（1）补充信息（市场调查表）价值多少？

（2）如何决策可以使利润期望值最大？

表2-19　销售情况概率

解：第一步，验前分析。该厂生产新产品有2种方案，即生产方案（a1）、不生产方案（a2），产品市场有3种状态，即好（θ1）、中（θ2）和差（θ3），状态θ的先验概率为

P（θ1）=0.25；P（θ2）=0.3；P（θ3）=0.45

于是，E（a1）=0.25×15+0.3×1+0.45×（-6）=1.35

E（a2）=0.25×0+0.3×0+0.45×0=0

由风险型决策的期望值准则得到验前最满意方案：无论市场结果如何，都要生产，最大期望收益值为1.35万元。

第二步，预验分析。要计算调查后的各个期望值，必须先计算概率P（Hi）和后验概率P（θj|Hi）。计算概率P（Hi），可把先验概率P（θj）和条件概率P（Hi|θj）代入全概率公式，求得

P（Hi）=P（θ1）P（Hi|θ1）+P（θ2）P（Hi|θ2）+P（θ3）P（Hi|θ3）

结果见表2-20。

表2-20　计算结果

计算后验概率P（θj|Hi），用贝叶斯公式

将上述有关概率值代入贝叶斯公式得表2-21。

表2-21　计算结果

由以上可以求得：当市场调查为H=H1时

E（a1）=0.575×15+0.266×1+0.159×（-6）=7.937

E（a2）=0

最大期望收益值 E（aopt|H1）=7.937

当H=H2时，E（a1）=0.236×15+0.509×1+0.255×（-6）=2.519

E（a2）=0

最大期望收益值E（aopt|H2）=2.519

当H=H3时，E（a1）=0.055×15+0.199×1+0.746×（-6）=-3.452

E（a2）=0

最大期望收益值 E（aopt|H3）=0

该企业通过市场调查所得的期望收益值

E=0.2825×7.937+0.2650×2.519+0.4525×0=2.91

由上可知，补充信息的价值是2.91-1.35=1.56（万元），取得市场调查表这个补充信息的费用是0.6万元，因此取得补充信息是值得的。

取得最大利润期望值的最优策略是进行市场调查，如果调查结果是新产品销路好或中等，则进行生产，否则就不生产。这个策略获得的期望利润为2.31万元。

第三步，验后分析。验后分析是把调查信息和验前信息结合起来，修正状态变量的先验分布，得到后验分布，并以此计算在调查信息发生的条件下，各可行方案的期望收益值，比较得到最满意的解决方案，这一计算过程预验分析已经完成。

综上所述，如果市场调查费不超过1.56万元，就应该进行市场调查，从而使企业新产品开发决策取得较好的经济效益。如果市场调查费用超过1.56万元，就不应该进行市场调查。该企业进行市场调查，如果销路好，就应该选择生产；如果销路情况中等，也应该生产；如果销路差，就选择不生产。