线性规划的理论和方法广泛地应用于经济、军事、工业、农业等各行业的计划安排、组织管理等方向的决策分析。线性规划是模型选优决策法的一种具体方法，线性规划的基本思想是在一组线性等式和不等式约束下求解线性函数的极值问题。下面，我们讨论线性规划模型的建立和问题模型的求解。

（一）线性规划模型的建立

如何合理地利用有限的资源取得最好的经济效果，是企业运营管理中经常出现的问题。线性规划是线性确定性条件下解决此类问题的有效方法，线性规划模型的建立即是将实际决策问题抽象转化为数学模型来处理。下面，我们通过一个实际生产计划最优化安排的例子来说明线性规划方法的应用。

【例2-2】设某厂生产3种不同型号的产品A、B、C，生产每种产品在各车间所需加工的工时，所产生的利润以及各车间的生产能力见表2-1。问该厂生产A、B、C 3种产品各多少单位，才能使工厂获得最大利润？

表2-1　例2-2中各车间产生的利润及生产能力表

解：设x1，x2，x3为生产A、B、C 3种产品的产量，则工厂所获得的利润为

c1、c2、c3为生产A、B、C 3种产品单位产品的利润。

生产3种产品所受的生产能力约束为

a11 x1+a12 x2+a13 x3≤b1

a21 x1+a22 x2+a23 x3≤b2

a31 x1+a32 x2+a33 x3≤b3

这样我们就得到了该厂生产量问题的线型规划模型：

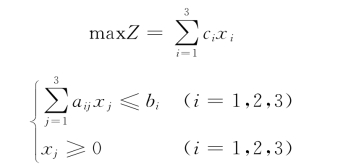
（二）线性规划问题的求解

建立了实际决策问题的线性规划模型之后，接下来的问题便是如何求线性规划模型的解，这里我们介绍线性规划模型求解的两种常用方法：图解法和单纯形法。

1.图解法

图解法，也称几何方法，是通过画平面图的形式来求解线性规划模型的解。图解法一般只适用于包括两个变量的线性规划问题。下面，我们举例说明。

【例2-3】某小型木材加工厂生产大桌子和小桌子两种家具。已有木材300板英尺，可利用的工时为140h。每种家具所需材料、工时以及所获利润见表2-2。

表2-2　每种家具的相关资料

试问该厂生产大桌子和小桌子各多少，才能使利润达到最大？用图解法求解。

解：设生产大桌子x1张，小桌子x2张，则问题的线性规划模型为

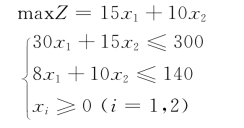
首先在平面直角坐标系中画出约束条件所决定的平面区域S，如图2-3所示。可以看到，平面区域S中的任何一点（x1，x2）均可以满足约束条件，称为可行解。现在要从这些可行解中找出使目标函数达到最大的最优解。本例的目标函数为Z=15x1+10x2，当Z值给定时，在平面直角坐标系中表示一条斜率为-1.5的直线，称为等值线。如果改变Z的值，等值线在平面内作平行移动。越向左下方移动，Z值越小，越向右上方移动，Z值越大。当等值线与区域S仅有一个公共点A时，Z值达到最大，点A的坐标为（5，10）即为最优解，最大利润值为Z=175元。

图2-3　约束条件决定的平面区域

【例2-4】某厂所生产的产品每桶500g，该产品由A和B两种配料合成。A材料5元/g，B材料8元/g。质量标准规定，每桶产品中含A不能超过400g，含B不能少于200g，求最低成本的配方。

变量：x1——材料A；x2——材料B

ACDB为可行解区（见图2-4），即由ACDB所构成的凸四边形上的任一点都能满足所有约束条件。

从可行解区求最优解，需结合目标函数进行综合分析。

图2-4　[例2-4]可行域图

令Z为不同的值代入上式，会得到一组斜率为-5/8的平行线，这组平行线中与凸多边形ACDB相交且距离原点最近的那条，与凸多边形ACDB相交于C点，为最优解。因为直线离原点越近，目标函数值越小。(www.daowen.com)

C点的坐标：x1=300，x2=200

Zmin=300×5+200×8=3100（元）

我们将图解法的一般步骤归纳如下：

（1）在平面直角坐标系内画出约束条件所确定的可行区域S。

（2）在平面直角坐标系内画出目标函数的一条等值线z0=c1 x1+c2 x2。

（3）在平面直角坐标系内与S相关的部分，移动目标函数的等值线使目标函数的值增大。

（4）当目标函数的值达到最大时，停止等值线的移动，记录下这时等值线与平面区域S的公共点坐标x*，即为最优解，这时的目标函数值z*即为最优目标值。

2.单纯形法

当变量数目达到2个以上时，采用画图的形式求解线性规划模型就变得越来越复杂，以至于难以解决。求解多个变量的线性规划问题，我们一般采用单纯形法。在多数情况下，经过有限次的逐次迭代，可以找到最优解。下面，来介绍单纯形法的具体应用。

【例2-5】某企业同时生产A和B 2种产品，每月电力消耗不超过240k W·h，设备不超过150台时，每吨产品电力、设备台时消耗定额见表2-3。

表2-3　消耗定额

A产品每吨可获利润2000元，B产品每吨可获利润4000元，两种产品各生产多少吨，可使企业在充分利用资源的条件下获利最多？

这个问题的线性规划模型结构如下：

变量：x1——A产品产量；x2——B产品产量

线性规划就是在满足一组约束条件下，求出一组变量的值，使目标函数达到最优。

把模型变为标准式：

引入松弛变量，把约束条件由不等式变为等式：

3x1+8x2+s1=240

6x1+3x2+s2=150

s1，s2为松弛变量，松弛变量不会带来利润，所以目标函数中松弛变量的系数是零：

Zmax=2000x1+4000x2+0s1+0s2

建立初始单纯形表，见表2-4。

表2-4　初始单纯形表

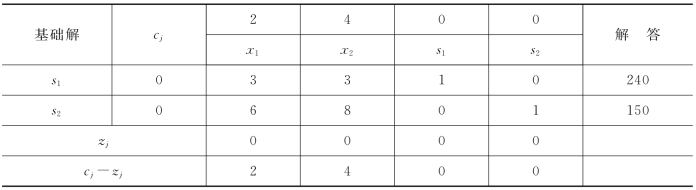
表中的基础解，表明变量的置换关系。在初始表里是松弛变量，在解题过程中，他们逐步被变量所取代。

cj——表示增加一个某变量的目标函数值；

zj——表示某个变量对目标函数值的影响；

cj-zj——以它来判别目标函数增加的可能性大小。若它是零或负值，表明目标函数已无增大的可能，最优解已经找到了。

解单纯形表，见表2-5。

表中最后一行cj-zj的数值均为零或负值，表明最优解已经找到，答案是

表2-5　解单纯形表

↑—关键列，由cj-zj的最大值决定；
←—关键行，由解答列与关键列数值的最小比值决定。