(一)直方图的概念

直方图又称质量分布图，是反映产品质量数据分布状态和波动规律的统计图表。直方图的主要用途是判断工序的稳定性、推断工序质量满足标准的程度。

直方图能形象、直观地表示产品质量的分布情况，用以整理质量数据，找出规律，通过对它的观察来分析、判断和预测产品质量的好坏，并进行适当地改进，解决其存在的问题。

(二)直方图的绘制

绘制直方图，将抽样检查得到的一批( 一般不小于100 个) 质量数据，编制频数分布表，具体工作包括找出该批数据的最大值和最小值，将数据按大小顺序分组，计算出组距、各组组界、各组的组中值，统计各组的数据个数，以组距为底边，以频数为高作出一系列直方形连接起来形成的图形。

例5:浆纱回潮率是浆纱的一个重要质量指标，其好否影响织造的断头率，某企业一品种最近布机断头增加，要分析浆纱回潮率对断头的影响，于是开展了以下工作。

(1) 收集数据。经测试获得某号纱线浆轴回潮率( %) 的数据如下( 一般要求不少于100 个数据，本例为了计算方便，采用了50 个数据) 。

(2) 计算平均数: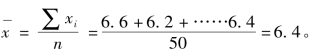

(3) 计算极差:R=xmax-xmin =6.7-6.1 =0.6。

(4) 确定分组数K 和组距h:K 取7，则组距

(5) 决定分组点。分组点的精度一般应比实验数据的精度多取一位小数，以防止有数据刚好落在分组边界上。

第一个分组点

第二个分组点=第一个分组点+组距=6.05 +0.1 =6.15；

第三个分组点=第二个分组点+组距=6.15 +0.1 =6.25；

……

(6) 作频数分布表，见表6-6。

表6-6　频数分布表(www.daowen.com)

(7) 以组距为底边，以频数为高画图，如图6-12 所示。

(三)直方图的分析

利用直方图分析质量一般分两步。先绘制直方图，再观察和分析直方图。观察直方图主要是为了对形态进行观察和分析，正常直方图必须满足下列三个条件。

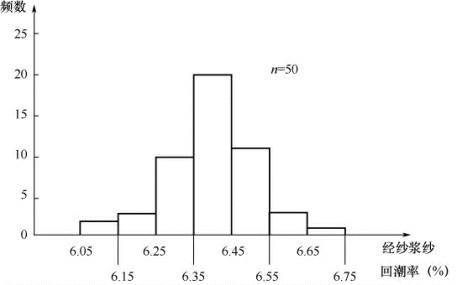
图6-12　浆轴回潮率(%)直方图

(1) 图形分布要中间高、两边低、左右对称。

(2) 图形中心与数据中心重合。

(3) 图形分布与标准上、下限之间有一定的余量。

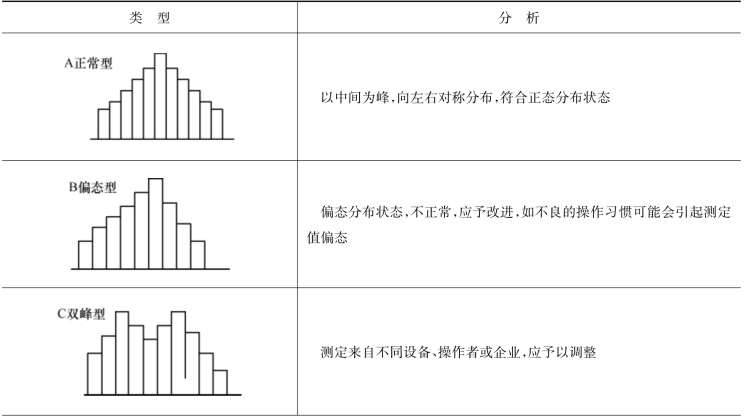
凡不同时具备正常直方图的三个条件者即为非正常直方图。非正常直方图的出现说明产品质量或生产过程已经处于非控制状态。常见的直方图类型见表6-7 的分析。

表6-7　直方图形状分析

续表

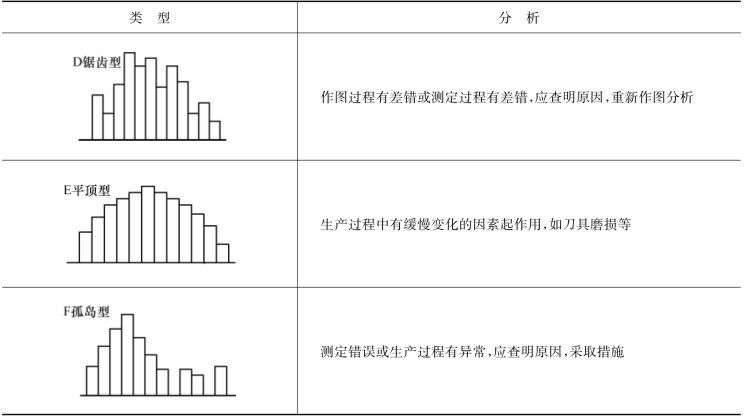
值得注意的是在观察分析直方图的整体形态的同时，还要将直方图与质量标准( 规格公差) 对比，借以判断工序对标准的适应能力和改善的余地。直方图分布范围与公差比较，如图6-13所示。图中B 是质量特性的实际分布范围，T 是质量标准的范围。

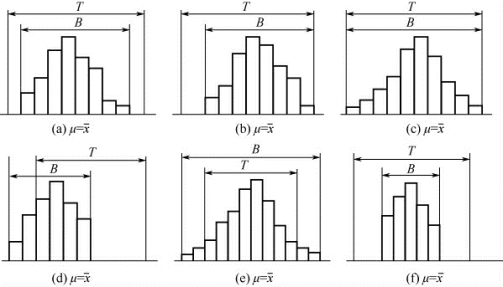
图6-13　直方图分布范围与公差比较图

图( a) 中，B 在T 中间，平均值又正好与公差中心重合，两侧有一定余地，表明工序质量稳定，不会出废品。图( b) 中，B 虽在T 内，但过于偏向一侧，有超下公差的危险，如加工条件稍有变动，就会出现不合格品。图( c) 中，B 与T 重合，表示工序能力毫无余地，存在两侧超差的危险。图( d) 中，B 的中心与T 的中心偏离太大，表示实际尺寸分布过于偏离公差中心，已经单边超差，出现不合格品。图( e) 中，B 大于T，虽然两中心重合，但两侧超差。表明工序能力太小，加工精度过低，尺寸的实际分布范围过大，超过了公差范围，必然出现不合格品。图( f) 中，B 与T 的中心重合，但两侧余地太大。表明工序稳定，但工序能力过于宽裕，经济性差。