货币时间价值是评价长期投资方案经济效益的重要因素。货币时间价值是指货币随着时间的推移而发生的价值“增值”。社会普遍认为，一笔货币如果作为储藏手段保存起来，在不存在通货膨胀因素的条件下经过一段时间后，作为同名货币，其价值不会有什么改变。但同样一笔货币若作为社会生产的资本或资金来运用，在通常情况下，经过一段时间后就会带来利润，使自身价值增值。从后一种情况看，同等数量的货币在不同时间上不能等量齐观。这就是所谓货币具有时间价值的现象。

西方对货币时间价值的定义是：由于放弃现在使用货币的机会所得到的按放弃时间长短计算的报酬。从货币时间价值原理可以看出：货币时间价值的形式是价值增值，是同一笔货币资金在不同时点上表现出来的价值差量或变动率；货币的自行增值是在其被当做投资资本的运用过程中实现的，不能被当做资本利用的货币是不具备自行增值属性的；货币时间价值量的规定性与时间的长短呈同方向变动关系。

1.一次性收付款项的终值与现值的计算

在某一特定时点上发生的某项一次性付款（或收款）业务，经过一段时间后再发生相应的一次性收款（或付款）业务，我们称为一次性收付款项。如存入银行一笔现金1 000元，年利率为10%，经过10年后一次取出本利和2 593 元，就属于这类一次性收付款项。这里若将存款当时的本金称作一次性收付款的现值，简记作P＝1 000 元，则n 期后的本利和就是一次性收付款的终值，简记作F＝2 593 元。也有人称一次性收付款的现值和终值为复利现值和复利终值。在考虑货币时间价值的情况下，现值与终值在价值上是等价的。

1）一次性收付款项终值的计算

已知现值P 和利率i，求n 期后的终值F 可按下式计算：

上式是由表7-1 所列示的P 与F 关系归纳出来的。

表7-1　P 与F 关系表

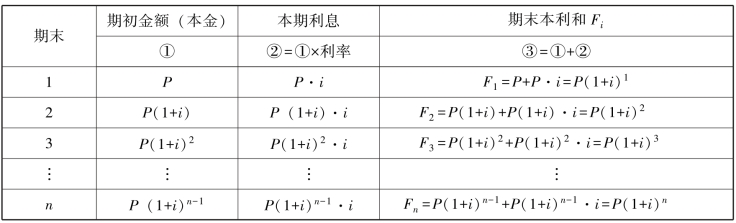
式中的（1＋i）n又叫一次性收付款项终值系数（又称复利终值系数，一元终值，终值因子），简称终值系数，记作（F/P，i，n）。根据不同的i 和n，计算出（1＋i）n＝（F/P，i，n）的值，列表即为终值系数表（见附表一：一元复利终值系数表）。于是式（7-1）可写成

由于查表可大大节约计算工作量，故式（7-2）更具有实用价值。

【例7-1】仍以上述存款业务为例，已知现值P＝1 000 元，利率i＝10%，存款期n＝10年。要求计算到期后的存款终值F。

解：

F（终值）＝P·（1＋i）n＝1 000×（1＋10%）10

＝2 593（元）

或

F＝P·(F/P，10%，10)＝1 000×2.593

＝2 593（元）

答：该项存款的到期值为2 593 元。

【例7-2】甲企业在年初存入一笔金额为10 万元的资金，已知年复利率6%。求3年后一次取出的本利和。

解：已知P＝10 万元，i＝6%，n＝3年

F（终值）＝P·（1＋i）n＝10×（1＋6%）3

＝11.91（万元）

答：3年后一次取出的本利和为11.91 万元。

2）一次性收付款项现值的计算

由本利和求本金的过程也叫折现，此时使用的利率i 又称折现率。折现是终值计算的逆运算，若已知未来终值F，折现率i 和期数n，则现值P 可按下式求出：

该式可由式（7-1）直接推得，式中（1＋i）-n叫一次性收付款项现值系数（又称复利现值系数，一元现值，现值因子），简称现值系数，记作（P/F，i，n）。该系数亦可通过查表求得（见附表二：一元复利现值系数表）。则有

显然，终值系数与现值系数互为倒数。

【例7-3】甲企业年初打算存入一笔资金，6年后一次取出本利和100 000 元，已知年复利率（折现率）为6%。要求计算企业现在应存入多少钱。

解：已知F＝100 000 元，i＝6%，n＝6年

P（现值）＝F·（1＋i）-n＝100 000×（1＋6%）-6

＝70 500（元）

或

P＝F(P/F，i，n)＝100 000×(P/F，6%，6)

＝100 000×0.705＝70 500（元）

答：企业年初应存入70 500 元。

【例7-4】假设甲厂准备自年初开始从利润留成中提取一笔资金，5年后一次取出，本利和共计60 万元。已知年复利率为6%。问该企业在年初应提取多少资金方能满足上述要求。

解：已知F＝60 万元，i＝6%，n＝5年

P（现值）＝F·（1＋i）-n＝60×（1＋6%）-5

＝44.82（万元）

答：该企业应在年初提取44.82 万元资金方能满足上述要求。

2.系列收付款的终值与现值

系列收付款的终值与现值，它是理解年金的终值与现值，以及递增（减）系列收付款终值与现值的基础。所谓系列收付款，是指在n 期内多次发生收（付）款业务，形成多时点收（付）款数列。

1）系列收付款的终值的计算

这一计算过程实际上就是将多时点资金数列逐一换算为未来某一时点的终值再求和的过程。如在n年内，已知每年年末存款Rt（t＝1，2，…，n），求第n年末一次取出的本利和一共是多少，这类问题就属于求系列收付款终值的问题。它是由一次性存款现值求终值的发展，即分别将不同时点存款的现值（当时值）按一定的复利率i 和该存款实际存放年限逐一换算为第n年末的终值，再将它们加起来，便得到系列存款的终值。

当系列收（付）款额为R1，R2，R3，…，Rn（Rt ≥0），它们相应的终值分别为F1，F2，F3，…，Fn时，该系列收（付）款的终值FR为

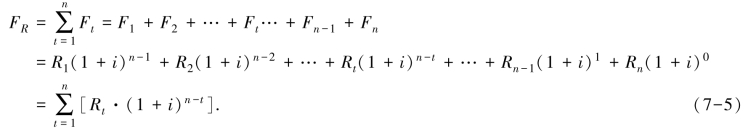
如果系列收（付）款不是在每年末发生，而是在年初，则系列收付款终值的计算公式应是

式（7-5）、式（7-6）中的（1＋i）n-t均为一次性收付款终值系数，所不同的是每当t 有一个确定值，便有一个（n-t）与之对应，可通过多次查终值系数表得到这些数值。故以上两公式又可分别写作

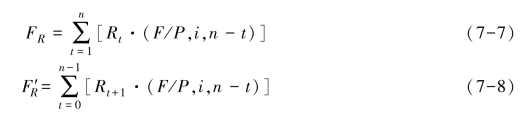
2）系列收付款的现值的计算

系列收付款的现值的计算实质上是将多时点的终值（当时值）统一换算为事前某一时点的现值再求其合计的过程。如在n年内每年末取款（本利和）Rt（t＝1，2，…，n），第n年取完，问事先应一次性存入银行多少钱才行（一次存入，分次取出）？ 这实际上是由一次性取款终值换算为现值问题的发展，只需将各期取款额（当期终值）分别折算为期初（第0年）的现值，那么这些现值的合计数就是所求的系列收入款项的现值。

设系列收付款分别为R1，R2，…，Rn（Rt ≥0），它们相应的现值分别为P1，P2，…，Pn时，系列收付款的现值PR为

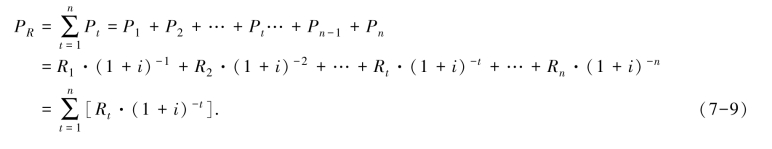
同理，上式亦可写成

系列收付款现值的计算在长期投资决策中是最常被采用的一种形式，应特别注意。

3.年金的终值与现值的计算

年金是系列收付款项的特殊形式，它是指在一定时期内每隔相同时间（如一年）就发生相同数额的系列收付款项，也称等额系列款项。

年金一般应同时满足下列两个条件：

（1）连续性。在一定期间内每隔一段时间必须发生一次收（付）款业务，形成系列，不得中断。

（2）等额性。各期发生的款项必须在数额上相等，因此若某系列收付款项Rt（t＝1，2，…，n）满足

Rt＋1＝Rt≡A，（t＝1，2，…，n-1，A 为常数）

则该系列收付款项便取得了年金形式，记作A。

在现实经济生活中，分期等额形成或发生的各种偿债基金、折旧费、养老金、保险金、租金、等额分期收付款、零存整取储蓄存款业务中的零存数、整存零取储蓄存款业务中的零取金额、定期发放的固定奖金、债券利息和优先股股息以及等额回收的投资额等，都属于年金的范畴。

年金又包括普通年金、先付年金、递延年金和永续年金等几种形式。其中普通年金应用最为广泛，其他几种年金均可在普通年金的基础上推算出来。因此应着重掌握普通年金的有关计算。

1）普通年金终值的计算

凡在每期期末发生的年金为普通年金，又叫后付年金，用A 表示。以后凡涉及年金问题若不特殊说明均指普通年金。普通年金终值又可简称年金终值，记作FA。它是特殊的系列收款终值，计算公式是

【例7-5】某企业连续10年于每年末存款5 000 元，年复利率为10%。要求计算第10年末可一次取出本利和多少钱。

解：根据题意，A＝5 000，n＝10，i＝10%

FA＝5 000×[（1＋10%）10-1]÷10%≈79 700（元）

答：第10年末可一次取出79 700 元。

式（7-11）中，FA/A＝[（1＋i）n-1]/i 叫年金终值系数（又称一元年金终值或年金终值因子），记作（FA/A，i，n），于是式（7-11）又可改写为

通过查一元年金终值系数表（见附表三：一元年金终值系数表）可以求得（FA/A，i，n）的值。

【例7-6】甲企业于每年年末向保险公司存入20 万元，为企业职工购买人身意外保险。年复利率为6%。要求计算第10年末该企业可以一次性取出的本利和。(www.daowen.com)

解：已知A＝20，n＝10，i＝6%，则

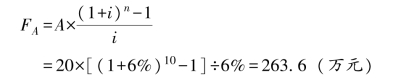
答：第10年年末该企业可以一次取出的本利和为263.6 万元。

2）年偿债基金的计算

年偿债基金的计算又叫积累基金的计算，即由已知的年金终值FA，求年金A（在此叫年偿债基金）的过程，它是年金终值的逆运算，亦属于已知整取求零存的问题。

由式（7-11）可直接求得有关公式

式中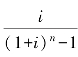，叫偿债基金系数，简记为（A/FA，i，n）。这个系数可通过查有关偿债基金系数表得到，或通过年金终值系数的倒数推算出来。

【例7-7】某企业计划在15年内每年末存入银行一笔资金，以便在第15年末归还一笔到期值为200 万元的长期负债。假设存款利率为8%。要求计算每年末应至少存多少钱。

解：已知FA＝200，n＝15，i＝8%

A＝FA·(A/FA，i，n)＝FA/(FA/A，i，n)

＝200÷（FA/A，8%，15）≈7.366 5（万元）

答：每年末至少应存入银行7.366 5 万元。

3）普通年金现值的计算

普通年金现值简称年金现值，它是等额系列收付款额现值的简化形式，记作PA。

由已知年金A，求年金现值PA的公式是

同理，PA/A＝[1-（1＋i）-n]/i 被称做年金现值系数（又叫一元年金现值或年金现值因子），记作（PA/A，i，n），亦可通过查一元年金现值系数表（见附表四：一元年金现值系数表）求之。则式（7-14）可写成

【例7-8】某企业打算连续12年在每年年末取出20 万元。年利率为8%。要求计算最初（第一年初）应一次存入多少钱。

解：根据题意，A＝20，n＝12，i＝8%

PA＝A·[1-(1＋i)-n]/i＝A·(PA/A，i，n)

＝20×（PA/A，8%，12）＝151.26（万元）

答：最初（第一年初）应一次存入151.26 万元。

【例7-9】甲企业若购置某自动化设备，每年可以节约人工和材料成本20 万元。设该设备的使用期为10年，年复利8%。要求计算该设备节约的人工和材料成本的现值。

解：根据题意，A＝20，n＝10，i＝8%

PA＝A·[1-(1＋i)-n]/i＝A·(PA/A，i，n)

＝20×（PA/A，8%，10）＝134.2（万元）

答：该设备节约的人工和材料成本的现值为134.2 万元。

4）年回收额的计算

这是年金现值的逆运算，即已知年金现值PA，求年金A（在此又称回收额），也就是已知整存求零取的问题。公式是

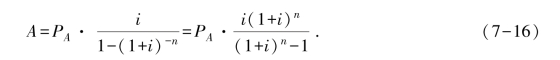
称作回收系数，记作（A/PA，i，n），可查有关的回收系数表，亦可利用年金现值系数的倒数求得。于是

【例7-10】某企业计划投资200 万元建设一个预计寿命期10年的新项目。若企业期望的资金报酬率为16%。要求计算企业每年末至少要从这个项目获得多少报酬。

解：这是一个已知年金现值PA＝200，n＝10，i＝16%，求年金A 的问题。

答：该企业每年末应从这个项目获得41.382 万元报酬。

5）其他种类年金问题简介

①先付年金的终值与现值的计算。

先付年金是在每期期初发生等额收付的一种年金形式，又称预付年金或即付年金，记作A′。其终值可在普通年金终值的计算公式基础上调整算出。先付年金终值F′A的公式是

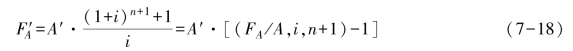
或

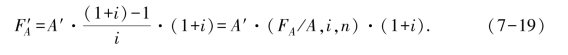
先付年金现值的计算公式是

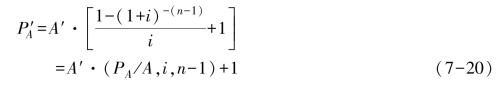
或

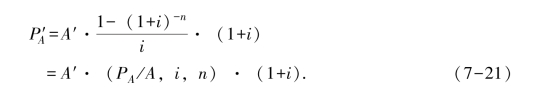
【例7-11】某企业连续5年于每年初存入银行200 万元，年复利率10%。要求计算到第5年年末可一次取出本利和多少钱。

解：依据题意，A′＝200，n＝5，i＝10%

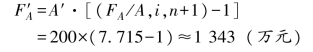
答：第5年末可一次取出1 343 万元。

【例7-12】某企业打算连续5年于年初投资200 万元建设一个项目。假定折现率为10%。要求计算当投资方式改为在第一年初一次投入全部投资额时，企业需投入多少资金才在价值上等于分次投资。

解：已知A＝200，n＝5，i＝10%，求先付年金现值。

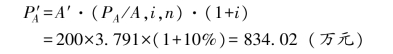
答：在第一年初一次投资834.02 万元的价值才等于连续5年于年初投资200 万元。

②递延年金现值的计算。

所谓递延年金是指在一定期间内（如n 期），从0 期开始隔s 期（s≥1）以后才发生系列等额收付款的一种年金形式，记作A″。显然，凡不是从第一年开始的年金都是递延年金。

递延年金现值的计算公式有两个：

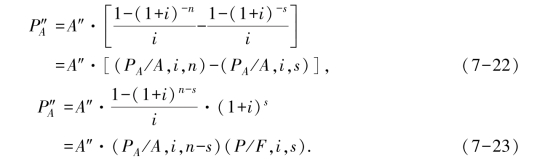
【例7-13】某企业年初存入一笔资金，从第6年年末起每年取出20 万元，至第10年末取完，年利率为10%。要求计算最初一次存入的款项是多少钱。

解：根据题意，A″＝20，n＝10，s＝5，i＝10%

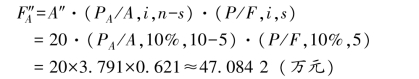
答：最初一次存入的款项是47.084 2 万元。

③永续年金现值的计算。

所谓永续年金是指无限等额支付的特种年金，即是当期限n→＋∞时的普通年金。在实际经济生活中，并不存在无限期永远支付的永续年金，但可以将利率较高、持续期限较长的年金视同永续年金计算。由于假设永续年金没有终点，故不存在其终值问题，只能计算其现值。公式为

由上式可十分方便地推算出永续年金的年金公式和利率的计算公式：

【例7-14】企业持有的甲公司股票每年股利收益为100 万元。假定企业不准备在近期转让该股票，甲公司的预期效益良好，并较为稳定。已知折现率为8%。要求对该项股票投资进行估价。

解：这是个求永续年金现值的问题。

根据题意，A＝100，i＝8%

答：该项股票投资估价为1 250 万元。

6）货币时间价值系数表的使用

我们已讨论了各种情况下如何利用货币时间价值的各种系数计算有关指标的问题。下面介绍货币时间价值系数表的使用。

①已知P，i，n，求F，利用（F/P，i，n），查一元复利终值系数表；

②已知F，i，n，求P，利用（P/F，i，n），查一元复利现值系数表；

③已知A，i，n，求FA，利用（FA/A，i，n），查一元年金终值系数表；

④已知A，i，n，求PA，利用（PA/A，i，n），查一元年金现值系数表。

上述问题的共性在于：首先判断属于哪类问题，再决定查什么系数表；查表时，按已知的i 和n 确定系数；然后将查得的系数与已知的有关金额相乘，便可计算出所求的有关项目的金额。

在长期投资决策方案评估中应用频率较高的系数表是复利现值系数表和年金现值系数表。