企业在同时生产几种产品的情况下，各种产品的生产量要受企业生产能力的限制，同时企业还要考虑产品的赢利能力，这就需要采用线性规划法对各产品生产数量进行规划，使现有生产能力得到最充分的利用。

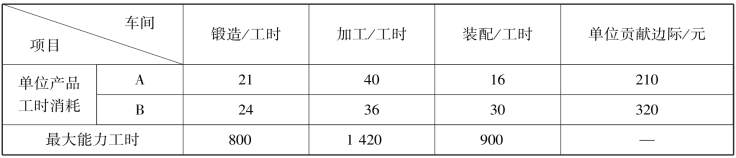
【例6-25】甲厂生产A、B 两种产品，每种产品都要经过锻造、加工、装配三个车间，各车间最大生产能力及单位产品需要的加工时间和赢利能力如表6-28所示。

要求就以下各不相关情况作出决策分析，使企业贡献边际最大。

（1）如何安排各种产品的产量，才能使生产能力得到充分利用？

（2）若各车间生产能力不生产A、B 产品而对外提供劳务，每一工时提供纯收入分别为：锻造车间2 元/工时，加工车间1 元/工时，装配车间3 元/工时，问：如何安排两种产品的产量，才能充分利用生产能力？

表6-28　产品及生产能力资料表

解：设A 产品产量为x 件，B 产品产量为y 件，贡献边际总额为S。

（1）生产能力无法转移时，要使生产能力得到充分利用的决策分析。根据上述资料有

将上述约束条件在坐标图上标出，如图6-5所示。

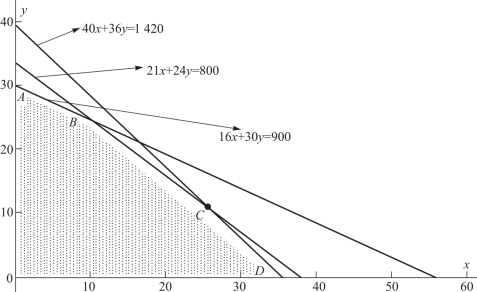
图6-5　线性规划图

在图中，ABCD 区域为可行解区域，各顶点的坐标分别为A（0，30）、B（9.75，24.80）、C（25.89，10.68）、D（35.5，0）。各顶点相应的贡献边际为(www.daowen.com)

SA＝210×0＋320×30＝9 600（元）

SB＝210×9.75＋320×24.80＝9 983.50（元）（极大值）

SC＝210×25.89＋320×10.68＝8 854.50（元）

SD＝210×35.5＋300×0＝7 455（元）

可见，能使贡献边际最大的可行解为B 点，取整后，即最优安排为A 产品生产9 件，B产品生产24 件，此时最大贡献边际约为9 753.10 元。

（2）在各车间生产能力可以对外出租的情况下，还应当考虑租金收入。依题意，对于可行解A（0，30）点来说，生产A 产品0 件B 产品30 件的组合，在锻造车间中尚剩余80个工时，在加工车间中尚剩余340 个工时，在装配车间中无生产能力剩余，共取得纯租金收入2×80＋1×340＝500（元）。同样道理，对于可行解B（9.75，24.80）点的生产组合来说，在锻造车间中无生产能力剩余，在加工车间中尚剩余137 个工时，在装配车间中无生产能力剩余，共取得纯租金收入2×137＝274（元）。在可行解C（25.89，10.68）点的生产组合下，在装配车间剩余165 个工时的生产能力，纯租金收入为3×165＝495（元）。在可行解D（35.5，0）点的生产组合下，在锻造车间剩余54 个工时，在加工车间中无生产能力剩余，在装配车间剩余332 个工时，共获租金纯收入为2×54＋3×332＝1 104（元）。因此各点的贡献边际总额分别为

SA＝9 600＋500＝10 100（元）

SB＝9 983.5＋274＝10 257.5（元）（极大值）

SC＝8 854.50＋495＝9 349.5（元）

SD＝7 455＋1 104＝8 559（元）

可以看出，考虑剩余生产能力出租后，B 点的组合即A 产品生产9.75 件、乙产品生产24.80 件为最优组合。上述分析也可以用下列公式表达

将各种生产组合下x 和y 的数值代入式（6-4），也可得到同样结果（因有关数字小数点之后被舍去，所以计算结果近似）。